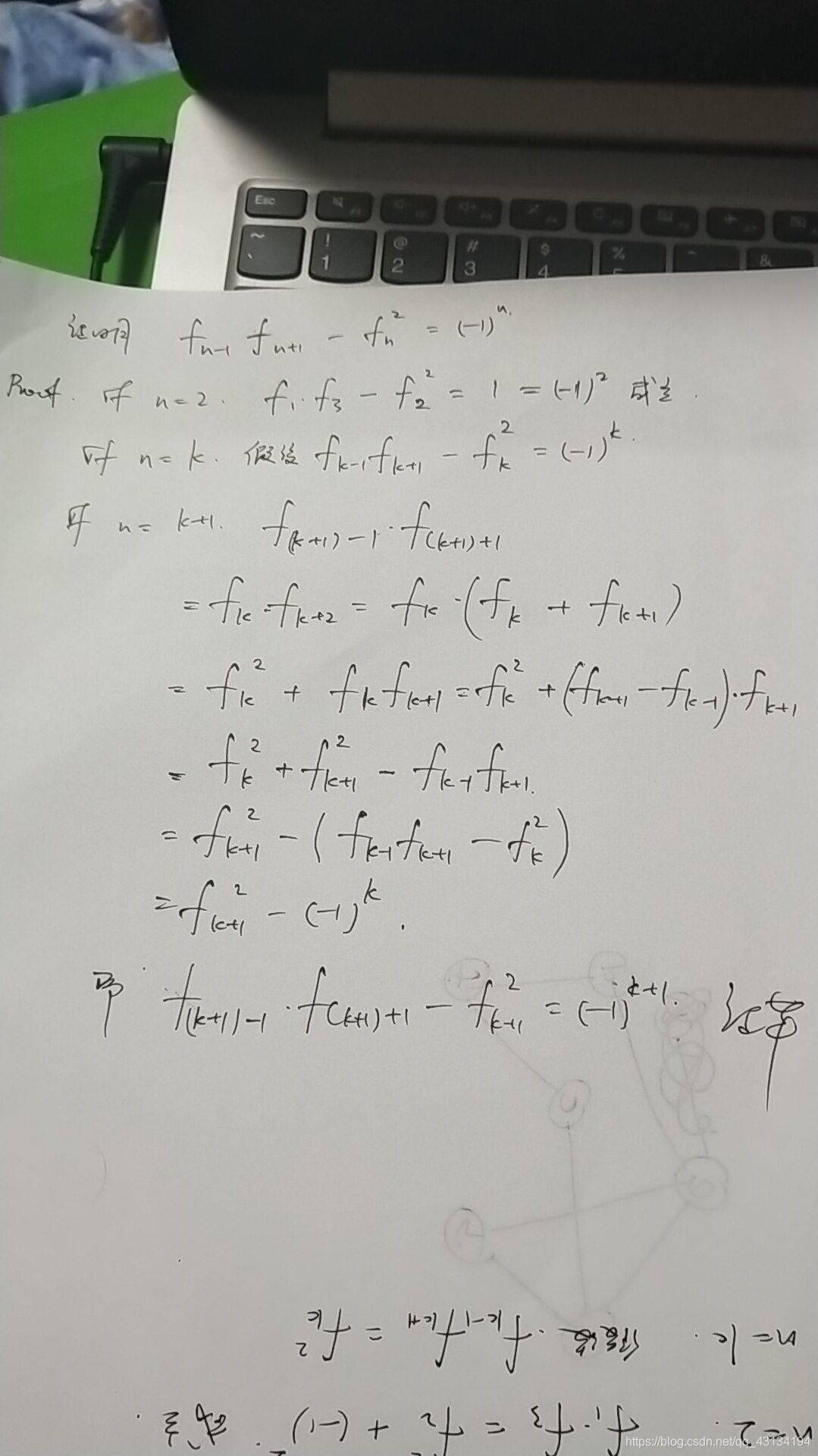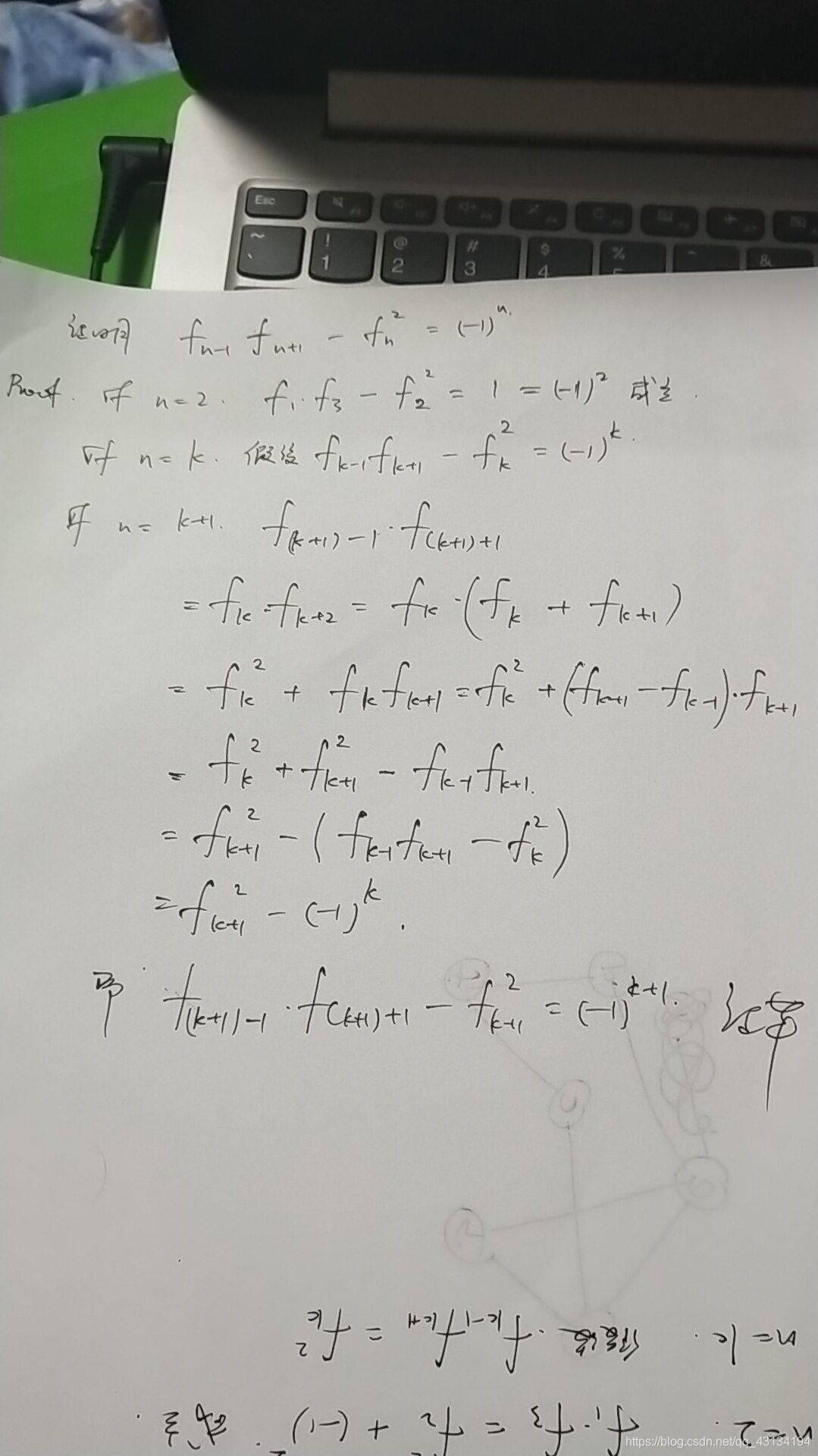斐波那契F(n+1)*F(n-1) - F(n^2) =(-1)^n的证明

证法一：

令 $A=\frac{1+\sqrt{5}}{2}$, $B=\frac{1-\sqrt{5}}{2}$

由斐波那契数列的通项公式 $F(n)=\frac{A^n+B^n}{\sqrt{5}}$可得

$F(n+1)F(n-1)= \frac{1}{5}(A^{n+1}+B^{n+1})(A^{n-1}+B^{n-1})$

$F(n)^2=\frac{1}{5}(A^n+B^n)^2$

证明：

$F(n+1)F(n-1)-F(n)^2$

$=-\frac{1}{5}(2A^nB^n-A^{n+1}B^{n-1}-A^{n-1}B^{n+1})$

$=-\frac{1}{5}[A^nB^{n-1}(B-A)-A^{n-1}B^n(A-B)]$

$=\frac{1}{5}(A-B)(A^nB^{n-1}+A^nB^n)$

$=\frac{1}{5}(A+B)(A-B)A^{n-1}B^{n-1}$

$=\frac{1}{5}*1*(-1)*(\frac{(1-\sqrt{5})*(1+\sqrt{5})}{2*2})^{n-1}$

$=(-1)*(-1)^{n-1}$

扫描二维码关注公众号，回复： 8748398 查看本文章

$=(-1)^n$

证法二：