密码学累加器cryptographic accumulator

1. 累加器概念

密码学累加器最早是由 Josh Benaloh 和 Michael de Mare 提出的，原始论文《One-way accumulators: A decentralized alternative to digital sinatures (extended abstract) 》[1] 于 1993 年发表在欧洲密码学会议（EUROCRYPT）上。这篇论文最初就是为了解决区块链上的数据可访问性问题而作的。

累加器可用于生成一个短的binding commitment to a set of elements together with short membership and/or non-membership proofs for any element in the set. 利用commitment，这些proofs可以publicly verified。

Merkle tree是最简单的累加器。

1.1 累加器的分类

累加器分为动态的和静态的：

• 动态累加器：当有元素加入或者移除时，commitment和membership proofs可以进行有效更新（所谓有效更新，是指更新的代价应与已累加的元素数量无关。）
• 静态累加器：当有元素加入或者移除时，commitment和membership proofs需总体重新生成，无法进行有效更新。

通用累加器都是动态累加器，且支持membership proof和non-membership proof。

1.2 累加器的实现假设

动态累加器的实现方式通常有：

• strong RSA assumption in groups of unknown order：如RSA group或者class group。[BP97,CL02, LLX07, Lip12]。最重要的前提是，集合内的所有元素必须相互co-prime，保证Bezout成立。
• bilinear maps：如[DT08, CKS09, Ngu05]。
• Merkle hash trees：如[Mer88, CHKO08]。

其中基于RSA和bilinear的动态累加器天然支持batching of membership proofs，但是不支持batching of non-membership proofs。在此基础上构建的Vector commitments（如[LY10, CF13, LRY16]）具有constant size openings，但是setup parameters非常large。

传统的累加器会引入一个可信任的第三方——accumulator manager，这个可信任的第三方拥有trapdoor可有效删除累加器中的元素，同时创建任意元素的membership witness。Lipmaa[Lip12]是第一个基于hidden order group构建不需要trusted setup的静态累加器。

1.3 累加器的常用语法和操作

上图中NonMemWitUp写错，应为：

NonMemWitUp $(A_t, u_x^t,x,upmsg)$

1.3.1 RSA累加器

补充MemWitUp和NonMemWitUp的算法细节如下：

MemWitUp $(A_t, w_x^t,x,upmsg)$

1. if: update membership proof for add:
2.   if: x==upmsg: return $w_x^t$
3.  else:
4.     $w_x^{t+1}=(w_x^t)^{upmsg}$
5.    return $w_x^{t+1}$
6. else if: update membership proof for delete:
7.   if: x==upmsg.x: return $\perp$
8.  else:
9.    choose (a,b) for $a*x+b*upmsg.x=1$ // $\because gcd(x,upmsg.x)=1$
10.    $w_x^{t+1} = (w_x^t)^b*(upmsg.A_{t+1})^a$
11.   return $w_x^{t+1}$
12. else: return $\perp$

NonMemWitUp $(A_t, u_x^t,x,upmsg)$

1. if: update NonMembership proof for add:
2.   if: x==upmsg: return $\perp$ //because x is now a membership.
3.  else:
4.     $A_{t+1}=(A_t)^{upmsg}$
5.     $a= u_x^t.a$
6.     $B= u_x^t.B$ // $\because A_t^a*B^x==g$
7.     choose (c,d) for $c*x+d*upmsg=1$ // $\because gcd(x,upmsg)=1$
8.     choose (a’,r) for $a'*upmsg=a-rx$ // $\because a*c*x+a*d*upmsg=a$
9.     $u_x^{t+1}=(a', B*A_t^r)$ // $\because {A_{t+1}^{a'}}*(B*A_t^r)^x==g$
10.    return $u_x^{t+1}$
11. else if: update NonMembership proof for delete:
12.   if: x==upmsg.x: return $\perp$ //because nonMembership element cannot be deleted.
13.  else:
14.     $A_{t+1}=upmsg.A_{t+1}$
15.     $A_{t}=upmsg.A_{t}$
16.     $x'=upmsg.x$ //It has $A_{t+1}^{x'}=A_t$.
17.     $a= u_x^t.a$
18.     $B= u_x^t.B$ // $\because A_t^a*B^x==g$
19.     choose (c,d) for $c*x+d*x'=1$ // $\because gcd(x,x')=1$
20.     choose (a’,r) for $a'=ax'+rx$ // $\because a*c*x+a*d*x'=a$
21.     $u_x^{t+1}=(a', B*A_{t+1}^{-r})$ // $\because {A_{t+1}^{a'}}*(B*A_{t+1}^{-r})^x==g$
22.    return $u_x^{t+1}$
23. else: return $\perp$

以上补充实际是结合2007年论文《Universal Accumulators with Efficient Nonmembership Proofs》得出的：

1.4 累加器的安全

累加器的不可否认性，即同一元素 $x$，不可能同时既在member proof中，又在non-member proof中。

1.5 累加器的构建

1.5.1 Bezout $(x,y)$

Bezout $(x,y)$是指，若 $x,y$互为素数，则存在 $a,b\in Z$，使得 $ax+by=1$成立。

1.5.2 ShamirTrick $(w_1,w_2,x,y)$

利用Bezout $(x,y)$来求 $(xy)-th$ root。具体实现细节为：
已知 $w_1^x=w_2^y=z$，有 $ax+by=1$，则有：
$z$的 $(xy)-th$ root为 $w_1^bw_2^a$。【 $\because (w_1^bw_2^a)^{xy}=z^{ax+by}=z$】

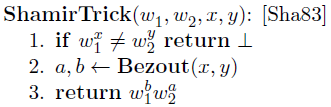
1.5.3 RootFactor $(g,x_1,...,x_n)$

已知 $y=g^x$，且 $x=x_1x_2...x_n$，求 $y$的 $x_i-th$ root，若直接计算的话，需要的算法复杂度为 $O(n^2)$，若采用RootFactor算法，则复杂度降为 $O(nlog(n))$：

2. Vector commitment

vector commitment（VC）具有与累加器完全相同的功能，但是对应的元素是有序的。A VC is a position binding commitment and can be opened at any position to a unique value with a short proof (sublinear in the length of the vector). The Merkle tree is a VC with logarithmic size openings. Subvector commitments [LM18] are VCs where a subset of the vector positions can be opened in a single short proof (sublinear in the size of the subset).

2018年论文《Batching Techniques for Accumulators with Applications to IOPs and Stateless Blockchains》中提出的VC算法，其subvector openings为constant size，public parameters也为constant size（与vector的长度无关）。若替换IOP中的Merkle-tree为该论文中的VC，则proof size 为 $O(r\lambda)$（其中 $r$为IOP rounds【在特殊的PCP中， $r=1$】， $\lambda$为Merkle tree的security parameter），与oracle queries的次数以及IOP proof oracles的最大长度均无关。

VC的binding特性中额外有position binding的要求：

具体可参见博客Vector Commitments代码实现。

3. IOPs（Interactive oracle proofs）

In an IOP the prover sends multiple proof oracles to a verifier. The verifier uses these oracles to query a small subsets of the proof, and afterwards accepts or rejects the proof. If the proof oracle is instantiated with a Merkle tree commitment and the verifier is public coin, then an IOP can be compiled into a non-interactive proof secure in the random oracle model [BCS16]. In particular, this compiler is used to build short non-interactive (zero-knowledge) proof of knowledge with a quasilinear prover and polylogarithmic verifier. Recent practical instantiations of proof systems from IOPs include Ligero [AHIV17], STARKs [BBHR18], and Aurora [BSCR+18].
IOPs采用Merkle trees而不是vector commitment。Merkle trees在该场景下有两个显著的缺陷：

• position openings为non constant size；
• 多个位置open时，无法压缩为一个constant size proof。（这些位置不是连续的，不是subvector commitment）。

参考资料：
[1] 1993年论文《One-Way Accumulators: A Decentralized Alternative to Digital Signatures (extended abstract)》
[2] 2007年论文《Compact E-Cash from Bounded Accumulator》
[3] 2008年论文《Practical Anonymous Divisible E-Cash From Bounded Accumulators?》
[4] 2002年论文《Dynamic Accumulators and Application to Efficient Revocation of Anonymous Credentials》
[5] 2005年论文《Accumulators from Bilinear Pairings and Applications to ID-based Ring Signatures and Group Membership Revocation》
[6] 区块链数据存储的“密码学黑科技”：累加器
[7] 2018年论文《Batching Techniques for Accumulators with Applications to IOPs and Stateless Blockchains》
[8] 2007年论文《Universal Accumulators with Efficient Nonmembership Proofs》