网络流建模选做
标签(空格分隔): 网络流 笔记
集合划分模型
概述
解决一类将集合划分为两类(因此是简化版的离散变量)的线性规划问题
其中划分在同/异集合的元素会在特定条件构成贡献
解决方法:
一般用一个虚拟点与条件限制点用一些特定方式连边后用割的容量来表示构不构成特殊条件
离散变量模型
概述
用于解决一类所求中两个或多个离散变量可以互相限制选择的线性规划问题
常见形式有差(和)的限制,选择先后限制
\(e.g.~for~\)离散变量:时间,高度
解决方法:
对于同一个变量的可能取值\(\{p_0,p_1,\cdots p_{m+1}\}\)(很多时候\(p_0\)表示开始,\(p_{m+1}\)表示结束,无实际意义)我们连边\((p_i,p_{i+1},val_{i+1})|i\in[0,m]\)
那么我们割掉边\((p_i,p_{i+1})\),花费\(val_{i+1}\)就代表这个变量取值\(i+1\)
对于变量之间限制,我们用\(INF\)的边来保证不合法的选点方案不是一个合法的割
【HNOI2013】切糕
简述
给一个\(n*m*h\)的立体图,对\(\forall(x,y)(1\le x\le n\vee1\le y\le m)\)要求选出\(1\le f_{x,y}\le h\)使得\(|f_{x,y}-f_{x',y'}|\le D(|x-x'+y-y'|=1)\),最小化\(\sum v_{x,y,f_{x,y}}\)
Solution
首先对每个离散变量\(f_{x,y}\),我们拆出\(h\)个点\(\{1,2,\cdots,h\}\)
然后连边
\((S,(x,y,1),v_{x,y,1})\)表示\(f_{x,y}=1\)
\(((x,y,i),(x,y,i+1),v_{x,y,i+1})(i\in[1,h))\)表示\(f_{x,y}=i+1\)
\(((x,y,h),T,INF)\)表示不能不选
然后考虑变量间限制
\(f_{x,y}-f_{x',y'}\le D\vee f_{x,y}-f_{x',y'}\le -D(|x-x'+y-y'|=1)\)
这里我们需要注意到割的性质:是让\(S,T\)分离的边
我们不能明确用割的容量去表示合法情况,那么就可以反其道而行用\(INF\)这个特殊的容量去禁止选一些情况
先给出结论
\(((x,y,k),(x',y',k-D),INF)(|x-x'+y-y'|=1)\)
什么意思,首先我们知道我们不能割这个边
如果你到达了\((x,y,k)\),你要跨越\((x,y)\)到\((x',y')\)并且选了\(f_{x',y'}<k-D\)
那么由于边\(((x,y,k),(x',y',k-D),INF)\)
妳割了\(((x',y',f_{x',y'}),(x',y',f_{x',y'}-1))\)但\((S,T)\)就联通,又因为你不可以割这条边,所以这个非法情况不是割
我们实际上满足了\(f_{x,y}-f_{x',y'}\le D\)
但很好理解\((x,y),(x',y')\)的关系有翻转的一天,也会满足满足了\(f_{x,y}-f_{x',y'}\le -D\)
Code
inline void Read(void){
re int i,j,k,last,dir,tx,ty;
n=read(),m=read(),H=read(),lim=read(),S=0,T=n*m*H+1,P=T+1;
for(k=1;k<=H;++k)
for(i=1;i<=n;++i)
for(j=1;j<=m;++j)a[i][j][k]=read();
for(i=1;i<=n;++i)
for(j=1;j<=m;++j){
last=S;
for(k=1;k<=H;++k)AddEdge(last,pos(i,j,k),a[i][j][k]),last=pos(i,j,k);
AddEdge(last,T,INF);
}
//同一个位置不同层可以从下往上传
for(i=1;i<=n;++i)
for(j=1;j<=m;++j)
for(k=1;k<=H-lim;++k){
for(dir=0;dir<4;++dir){
tx=i+dx[dir],ty=j+dy[dir];
if(tx>n||!tx||!ty||ty>m)continue;
AddEdge(pos(tx,ty,k+lim),pos(i,j,k),INF);//从上到下,只要高于这个就必须割INF
//事实上(i,j)也会被连一个来限制下界
}
}
}【Srm590】Fox And City
简述
为一个无向图任意加边求\(\sum_{i\in V}(dist_{1,i}-w_i)^2\)最小值
Solution
实际上跟\(Fee\_cle6418\)的方法是一样的,只不过少了一个优化
首先对于每一个离散变量\(dist_{1,i}(i\in V)\)取值为\([0,n)\)(除了\(dist_{1,1}\))
于是我们对\(1\)外的点仍然从小到大串起来,但不在这个时候表示他的选择
\((S,(i,0),INF)\)
\(((i,k),(i,k+1),(x-(k+1))^2)(k\in[0,n-1))\)
\(((i,n-1),T,INF)\)
做一个解释虽然我们常说\(p_0\)就是开始(常为\(S\)),但这个时候的\((i,0)\)才表示开始,因为除了\(1\)外\(dist\)都不可为\(0\)
证明两个事情
- 加边只会让\(dist\)变小(
没用) - 加对于一对有边相连的点\((x,y)\)无论如何加边\(|dist_{1,x}-dist_{1,y}|\le 1\)
这就是切糕的套路(懒得再解释)
若\(\exists(x,y)\),连边\(((x,k),(y,k-1),INF)\&((y,k),(x,k-1),INF)\)
单独考虑\(1\)
因为\(dist_{1,i}\)不能不为\(0\)
所以\(((1,k),(1,k+1),INF)(k\in [0,n-1))\)
\(((1,n-1),T,INF)\)
同时\((1,0)\)不表示开始(它本身合法),因此不连\(S\)
感性理解一下上面那句话:连上这条边\(S,T\)永远有路
实际上用刚才第一个性质可以在连通图特殊情况下优化边数那就是最短路只会减小
【无来源】矩形
简述
为一个\(n*m\)的矩形每个位置填数\([0,9]\),使得相邻格子和不超过给定数,求最大数字和
Solution
考虑这道题与上一道区别:和的模型,以及求的变为了最大值
但我们并不能黑白染色(欢迎教我题解上面写的怎么做),因为我们实际上是在选择离散变量
我先给出我的做法
首先权值取负并\(+10\)(割的边数是定的)
然后我们这样连边
\((S,(x,y,9),10-v_{x,y,9})\)
\(((x,y,k),(x,y,k-1),10-v_{x,y,k-1})\)
\(((x,y,0),T,INF)\)
如果你细心你会发现实际上我是在将离散变量从大向小连边
紧接着\(((x,y,k),(x',y',(D-k)))(|x-x'+y-y'|=1)\)
有了上题的经验,这里不再描述,直接给出结论性理由
对于可到达点\((x,y,k)\)
若\((x',y',w)\)有\(w+k>D\)那么这个点在上面被割掉,\(S,T\)依然联通,不是一个可行割
这样就保证了\(k\)一定\(w+k\le D\)
翻转过来亦然
实际上我看懂他的方法了
先黑白染色
对于白点\((S,(x,y,0),10-v_{x,y,0})\)
\(((x,y,k),(x,y,k+1),10-v_{x,y,k+1})\)从小向大串
对黑点则\(((x,y,k),(x,y,k-1),10-v_{x,y,k-1})\)从大向小串
\(((x,y,0),T,INF)\)
那么强制白到黑
再\((x,y,k),(x',y',D-k),INF((x+y)\%2=0\vee (x'+y')\%2=1)\)
原理跟上面是一样的只不过少建了一半的边
【BJOI2016】水晶
简述
六边形网格中有能量源(\((x+y+z)\%3=0\)时),\(n\)个水晶,炸一些水晶,使得
- 没有水晶三元环
- 没有水晶串能源

求最大剩余权值和
Solution
这题没有刚才的裸,我们要找到离散变量
首先六边形很讨厌,我们可以轻易的将其转为矩形\((x,y,z)\rightarrow (x-z,y-z)\)
然后对除了能量源的点黑白(红绿)染色,那么构成共振当且仅当存在一个能量源六联通格子被选的有黑白两色
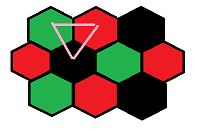
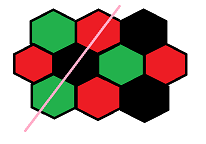
因此这个里面的离散变量(仅对于能量源)为\(\{\)去黑,去白,去能量源\(\}\)
实际上这道题的离散变量并非一个具体点选择,而是一个决策
我们拆能量源入/出
\(((x',y'),(x,y),INF)((x'+y')\%3=1\vee(x+y)\%3=0\vee(x,y)相邻(x',y'))\)
\(((x,y)',(x',y'),INF)((x'+y')\%3=2\vee(x+y)\%3=0\vee(x,y)相邻(x',y'))\)
表示只要\((x,y)\)和\((x',y')\)同时选就始终存在\((S,T)\)通路
其余就是黑白染色套路
\((S,(x,y),v_{x,y})((x+y)\%3=1)\)
\(((x,y),T,v_{x,y})((x+y)\%3=2)\)
\(((x,y),(x,y)',1.1v_{x,y})((x+y)\%3=0)\)
Code
inline void Read(void){
re int i,z,v,tmp,dir,tx,ty;n=read(),S=0,T=n<<1|1,P=T+1;
for(i=1;i<=n;++i){
x[i]=read(),y[i]=read(),z=read(),v=read();x[i]-=z,y[i]-=z;
ans+=(r[i]=((x[i]+y[i])%3)?v*10:v*11);
if(!hash[res=Find(x[i],y[i])])hash[res]=i,val[res]=r[i];else val[res]+=r[i],again[i]=1;
}
for(i=1;i<=n;++i)if(!again[i]){
tmp=((x[i]+y[i])%3+3)%3;
if(!tmp)AddEdge(i,i+n,val[Find(x[i],y[i])]);
if(tmp==1)AddEdge(S,i+n,val[Find(x[i],y[i])]);
if(tmp==2)AddEdge(i,T,val[Find(x[i],y[i])]);
}
for(i=1;i<=n;++i)if(!again[i]){
for(dir=0;dir<6;++dir){
tx=x[i]+dx[dir],ty=y[i]+dy[dir];
res=hash[Find(tx,ty)];if(!res)continue;
if(((tx+ty)%3+3)%3==0&&((x[i]+y[i])%3+3)%3==1)AddEdge(i+n,res,INF);//1连
if(((tx+ty)%3+3)%3==2&&((x[i]+y[i])%3+3)%3==0)AddEdge(i+n,res,INF);
}
}
}小结
总的来说离散变量模型选用最小割的意义在于选择
做题步骤一般为:
- 转化问题找出离散变量
- 具体数值,那么先定单变量顺序,后定变量间贡献
- 决策,那么分情况讨论,看什么时候合法
