【反馈】过程模型和反馈架构

本文链接： https://blog.csdn.net/weixin_41374099/article/details/101190712

过程模型

自我调节过程

给出一个简单模型，其输入是阶跃信号，系统对输入变化发生响应并接近稳定状态。可能经历的延迟，但系统输出没有出现冲击或振荡。由于模型（或叫系统）最终停留在稳定状态，所以这种过程称为自我调节。
在这里插入图片描述
如果忽略 $t\rightarrow τ$ 这段，那么模型就可以用下面的式子表示
$f_1(t)= \begin{cases} K(1-e^{-(t-τ)/T}) ,t>τ\\0 ,other \end{cases}$

根据上一篇传递函数，这时的传递函数为 $H_1(s)=\frac{K}{1+sT}e^{-sτ}$ ，

考虑复杂点，那么 $τ$ 不是死区。使曲线在 $t\rightarrow τ$ 之间能显示出过渡角
$f_2(t)=\begin{cases} K\left[ 1-(1+\frac{t-τ}{T})e^{-(t-τ)/T} \right] ,t>τ \\0,other \end{cases}$
此时的传递函数为 $H_2(s)=\frac{K}{(1+sT)^2}e^{sτ}$

当然，两个模型都不一定能准确描绘曲线，都是自己设定的，参数也需要自己去调。

带有振荡的自我调节过程

一个典型的具有振荡的阶梯反应模型是：
$f(t)=K\left[ 1-e^{-\zeta\omega t}(\zeta\frac{\omega_0}{\omega}sin\omega t+cos\omega t) \right]$
$\omega_0$ 是系统的固有频率， $\zeta$ 是阻尼因子（振荡幅度大时因子小）, $\omega = \omega_0\sqrt{1-\zeta^2}$ 。这种过程在计算机系统或者工业过程中很少见，但是在机械和电气设备中很多。这个模型对应的频域为 $F(s)=\frac{K\omega_0^2}{s^2+2\zeta\omega_0 +\omega_0^2}$

累积过程

在这里插入图片描述
累积过程对应着上一篇中的斜坡输入，自我调节对应着简单的阶梯输入，这两个都是简单模型。上面模型有三个参数，延迟 $τ$ ，时间常数 $T$ , 速度增益 $V$

忽略T内的变化，用一条斜线来简化这个模型
$f_1(t)=\begin{cases} V(t-τ),t>τ\\0,other \end{cases}$
频域下： $H_1(s)=\frac{V}{s}e^{-sτ}$

尝试描述T内的变化，
$f_2(t)=\begin{cases} V[ t-τ - T(1-e^{-(t-τ)/T}) ] \\0,other \end{cases}$
频域下： $H_2(s)=\frac{V}{s(1+sT)}e^{-sτ}$

非最小相位系统

在这里插入图片描述
这种系统对控制输入的初始反应是和控制输入相反的走向。

通用反馈架构

在这里插入图片描述
K控制器，H系统，G回路过滤器。d负载干扰，n测量噪声。

该图中显示了测量噪声，它是作为外部信号n被加到系统输出中的。模型中的负载扰动d影响了系统输入u，但是我们无法观察到负载扰动。这是理想化的建模，实际上干扰也许是从系统内部产生的，捕获这种行为需要为随时间变化的系统H建模。只要观察不到的干扰，我们都把它视为系统输入的部分，可以认为系统本身是静态的。

改变运行条件：增益调度

有时，控制回路需要在较宽的范围内的不同条件下运行，需要激发控制系统的不同行为，因此控制器增益需要不同的值。根据适当的调度信号的值，让增益参数自由地浮动。
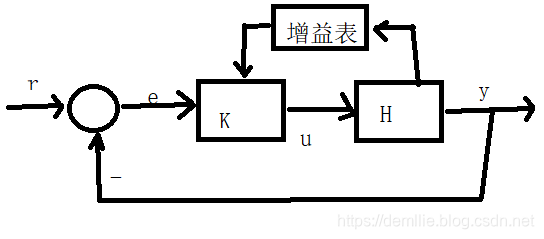
在这里插入图片描述

强干扰：前馈

当反馈系统遭受到突然的强干扰时，有时可以通过直接的前馈控制策略来扩展反馈回路的“自动”控制。

因为反馈控制的工作原理是响应误差，这种控制适用于幅度小而频繁的偏差。如果是突然的强干扰，通过反馈循环减少误差的措施达不到快速有效。

前馈控制可以帮助避免突然变化的不期望的影响，但过分依赖前馈控制会削弱前面讨论的反馈控制的优点。所以应该谨慎使用前馈。

在这里插入图片描述

快_慢动态特性：嵌套或“级联”控制

有时，我们需要控制回路具有自然缓慢的动态特性等。这时如果有响应很快的子过程，那么就可以通过级联或者嵌套来提高系统的性能。

比如：有这样一个任务服务器的例子，我们想要控制的过程变量是队列中请求的平均时间，然而得到这个数量的响应比较慢，因为它是根据目前正在等待的所有请求，计算出它们的平均等待时间。同时必须控制在短期内排队的长度，防止队列溢出。

通过嵌套两个控制循环来解决这个问题。内部的快速循环监视队列的长度，调整活动工作单位的数量。外部的慢循环跟踪平均等待时间，将调整后的队列长度作为设定值，传递给内部循环。

在这里插入图片描述

延迟系统：史密斯预报器

滞后系统会在激励后有马上的反应，而延迟系统却要等待一段时间，后者更难控制。是不是延迟系统不是自己决定的，而是由现实的限制。如果能够减少延迟 $τ$ 到忽略延迟，谁还需要这么复杂的系统呢？

一个具有延迟的系统的响应由两部分组成，一是在延迟一段时间期间没有任何事发生，二是过程的实际动态响应，一旦延迟过去就立马在输出中看到变化。
在这里插入图片描述
内圈循环：控制器 $\rightarrow$ 模型 $\rightarrow e=r-v$ , 这是普通的闭合反馈回路。此时控制器控制的是模型而不是（带有延迟的）系统,这是模型输出 $v$ 跟踪设定值 $r$ 的效果。
另外，控制信号也发送给实际系统H，所以如果H没有延迟，它将和模型表现（近似）一致。实践中真实系统会受到随机的干扰，而模型不会，为了矫正差异，引入第二个反馈回路。

外圈循环：控制器 $\rightarrow$ 系统和延迟 $\rightarrow y$
控制器 $\rightarrow$ 模型 $\rightarrow$ 延迟 $\rightarrow w$
$\rightarrow e=w-y$
单单是外圈反馈的影响的话，就是系统输出 $y$ 跟踪设定值 $w$ 的效果。 $w \&y$ 的差值就是理论模型加延迟与实际的系统之间的建模误差。结合外圈内圈的反馈就可以得到具有控制延迟系统的控制反馈回路了。

史密斯预报器的另一种结构如下，同样有延迟、内外反馈、输入( $e=r-y+w-v$ ) ……
在这里插入图片描述

来自《企业级编程与控制理论》