CF26D Tickets 期望，概率复习

~~说是复习其实这道题的知识点我没学过~~

核心我是看这篇博客学会的

\(Firstly\),转化题面

现在在\((k,0)\)的位置

每次可以向上走一步或向右走一步

即从\((a,b)\)可以到\((a+1,b)\)或\((a,b+1)\)

要求不能过\(f(x)=x\)

求走到\((n+k,m)\)的方法数\(P\)

\(Secondly\),方法

如图从\(B(k,0)\)走到\(A(n+k,m)\)

先不考虑不能过\(f(x)=x\)

方法数易得：

\[C_{n+m}^{m}\]

然后再算过了的相减就得\(P\)

我们找\(C\)点

\(C\)与\(B\)关于\(f(x)=x+1\)对称

可得\(c(-1,k+1)\)

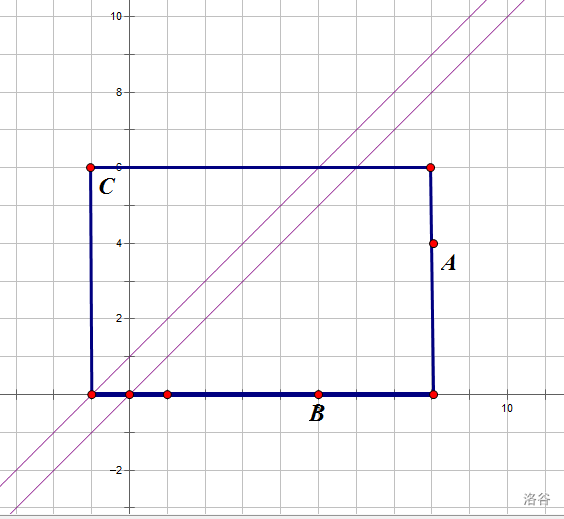
只要 B到A是经过了\(f(x)=x\)的

那么一定有一条对应的\(C\)到\(A\)的路径

证明：

如果\(B\)到\(A\)的路径过\(f(x)=x\)

那么\(B\)到\(A\)的路径一定过\(f(x)=x+1\)或有点在\(f(x)=x+1\)上

如图 \(D\)点一定存在

定义\(g(a,b)\)为从\(a\)点到\(b\)点的方法数

则\(g(c,d)=g(b,d)\)

一定有\(g(d,a)=g(d,a)\)

所以只要 B到A是经过了\(f(x)=x\)的

那么一定有一条对应的\(C\)到\(A\)的路径

现在就可以得出

\[P=C_{n+m}^{m}-g(c,a)=C_{n+m}^{m}-C_{n+m}^{m-k-1}\]

再除以方案总数化简可得

\[1-\frac{\displaystyle\prod_{i=m-k}^{m}i}{\displaystyle\prod_{j=n+1}^{n+k+1}j}\]

\(Code\)

#include <map>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define reg register int
#define isdigit(x) ('0' <= (x)&&(x) <= '9')
template<typename T>
inline T Read(T Type)
{
    T x = 0,f = 1;
    char a = getchar();
    while(!isdigit(a)) {if(a == '-') f = -1;a = getchar();}
    while(isdigit(a)) {x = (x << 1) + (x << 3) + (a ^ '0');a = getchar();}
    return x * f;
}
double ans = 1.0;
int main()
{
    int n = Read(1),m = Read(1),k = Read(1);
    if(n + k >= m)
    {
        for(reg i = 1;i <= k + 1;i++)
            ans *= (double)(i + m - k - 1) / (n + i);
        printf("%.5lf",1.0 - ans);
    } else printf("0");
    return 0;
}