\(T1\) 排队
Description
抢饭是高中生活的一部分,现在有一列队伍长度为 \(n\),(注意:由于人与人之间要保持距离,且不同情况所保持的距离大小不同,所以长度并不能直接体现队列的人数)。已知男男之间的距离为 \(a\),男女之间距离为 bb,女女之间距离为 \(c\)。一个男生打饭时间为 \(d\),一个女生打饭时间为 \(e\),求所有情况的排队时间总和(忽略身体的大小对队伍长度的贡献),答案对 $10^{9}+7 $取模。
Input Format
一行六个整数 \(n\), \(a\), \(b\), \(c\), \(d\), \(e\)。
Output
一行一个整数,即答案。
Solution
首先我们很容易想到一个DP做法,这里我们构造 \(f\) \([i][0/1]\)数组,表示最后一个人是0/1的情况下,最后一个人打到饭的时间之和,0表示最后一个人是男生,1是女生。
定义g\([i][0/1]\)表示最后一个人是 的情况下的总方案数。手推得状态转移方程:
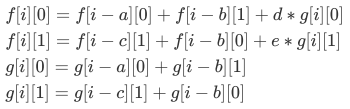
但我们会发现\(n\)非常的大,但是\(a\),\(b\),\(c\),却很小,因此每次转移时所需要的\(i-a\),\(i-b\),\(i-c\)非常靠近 ,因此可以考虑使用滚动数组转移。
但滚动数组并没有对时间上做出优化。
这里的转移我们用矩阵乘法来代替,只需构造一个\(4*max(a,b,c)\)阶的转移矩阵即可。
下面我们来详细说一说这个矩阵的构造!!
首先看到\(g\)数组对\(f\)数组的转移造成了影响,所以我们在矩阵中不仅只转移\(f\),还必须加入\(g\)的转移。
按照常理,构造出的初始矩阵长这样:

但考虑到 \(f\) \([i][0/1]\)和g\([i][0/1]\)这四个必须一起转移的东东,所以每个\(i\)要维护四个值,所以在每一个块中维护四个值,所以变成了:

好了,这样就可以解释为什么是\(4*max(a,b,c)\)阶了, 阶就是矩阵长宽的意思啦
然后的矩阵构造就为了一个目标:
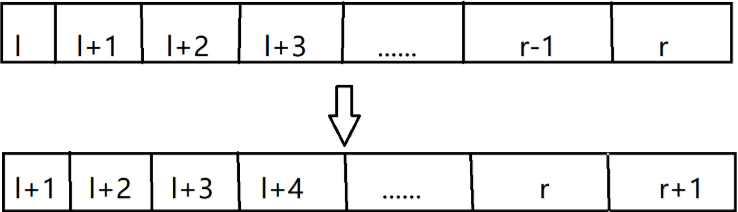
这个的意思就是从\(r\)推出\(r+1\),然后对着这个和上面的dp转移方程构造一个转移矩阵就好了.
形如:

构造完成后就将转移矩阵快速幂,快速得到最后的答案 \(f[n][0]\)+\(f[n][1]\)
细节:代码实现时因为是每四个当成一块,所以我们用 \(<<2\)(等价于乘4)也可以迅速得到每个i对应矩阵中的位置,每一块中的选择则用 |(或操作=加操作)来处理,使代码简洁。
#include<bits/stdc++.h>
#define ll long long
#define N 150
using namespace std;
const int mod=1e9+7;
ll n;
int a,b,c,d,e,O;
int g[N][2],f[N][2];// f[i][0/1]表示长度为i的队伍最后为男生(0)或女生(1)的答案 g[i][1/0]与f一样,不过是记录到达这个状态的方案数
struct Matrix{
int a[N][N];
Matrix(){memset(a,0,sizeof(a));}
}T,qs,asd;//T为转移矩阵 qs为初始矩阵
void mul(Matrix &CC,Matrix A,Matrix B)
{
Matrix C;
int i,j;
for(i=0;i<O;i++)
for(j=0;j<O;j++)
C.a[i][j]=0;
for(i=0;i<O;i++) //两个矩阵的相乘
for(j=0;j<O;j++)
if(A.a[i][j])
{
for(int k=0;k<O;k++)
if(B.a[j][k])
C.a[i][k]=(1ll*A.a[i][j]*B.a[j][k]+C.a[i][k])%mod;
}
CC=C;
}
void Ksm(Matrix &CC,Matrix AA,ll t) //标准快速幂
{
Matrix A,C;
t--;
A=C=AA;
while(t)
{
if(t&1)
{
mul(C,C,A);
}
mul(A,A,A);
t>>=1;
}
CC=C;
}
int main()
{
int i,j;
scanf("%lld",&n);
scanf("%d%d%d%d%d",&a,&b,&c,&d,&e);
g[0][0]=g[0][1]=1; //初始化
f[0][0]=d,f[0][1]=e; //初始化
int o=max(a,max(b,c)); //转移所需的最小的矩阵
O=o<<2;//矩阵长宽
for(i=1;i<o;i++)// 初始化第一个矩阵
{
if(i>=a) (f[i][0]+=f[i-a][0])%mod,(g[i][0]+=g[i-a][0])%mod;
if(i>=b) (f[i][0]+=f[i-b][1])%mod,(g[i][0]+=g[i-b][1])%mod,(f[i][1]+=f[i-b][0])%mod,(g[i][1]+=g[i-b][0])%mod;
if(i>=c) (f[i][1]+=f[i-c][1])%mod,(g[i][1]+=g[i-c][1])%mod;
f[i][0]=(1ll*g[i][0]*d+f[i][0])%mod;
f[i][1]=(1ll*g[i][1]*e+f[i][1])%mod;
}
//下面开始把我们构造的转移矩阵完善一下
for(i=1;i<o;i++)
{
for(j=0;j<4;j++)
T.a[i<<2|j][(i-1)<<2|j]=1; //把矩阵中的1全填了再说
}
T.a[(o-b)<<2][(o-1)<<2|1] = T.a[(o-b)<<2|2][(o-1)<<2|3] = T.a[(o-b)<<2|1][(o-1)<<2] = T.a[(o-b)<<2|3][(o-1)<<2|2] = 1; //把公式中的全部i-b的影响填上1
T.a[(o-b)<<2|2][(o-1)<<2|1] = e; T.a[(o-b)<<2|3][(o-1)<<2] = d; //把e和d填上
//后面也在一个一个填数
++T.a[(o-a)<<2][(o-1)<<2]; ++T.a[(o-a)<<2|2][(o-1)<<2|2];
(T.a[(o-a)<<2|2][(o-1)<<2]+=d)%mod;
++T.a[(o-c)<<2|1][(o-1)<<2|1]; ++T.a[(o-c)<<2|3][(o-1)<<2|3];
(T.a[(o-c)<<2|3][(o-1)<<2|1]+=e)%mod;
for(i=0;i<o;i++) //把之前求出的初始f付给这个初始矩阵
{
qs.a[0][i<<2] = f[i][0];
qs.a[0][i<<2|1] = f[i][1];
qs.a[0][i<<2|2] = g[i][0];
qs.a[0][i<<2|3] = g[i][1];
}
Ksm(T,T,n-o+1); mul(qs,qs,T); //快速转移
printf("%d\n",(qs.a[0][(o-1)<<2]+qs.a[0][(o-1)<<2|1])%mod); //取最后的答案
return 0;
}