转载自https://blog.csdn.net/wh2124335/article/details/8871535?locationNum=14&fps=1
一、佩尔方程的形式:
$$x^2-Dy^2=1,\ D为正整数$$
二、关于佩尔方程的特解
特解是指佩尔方程的最小整数解,容易发现当x最小的时候y也同样达到最小。
在一般情况下,佩尔方程的特解是通过暴利枚举方法得到的,本文将介绍如何用应用连分数法求特解。
本文将不涉及证明,只介绍方法。
三、连分数法
一个实数的简单连分数表示,是指将一个实数用以下方法表示:
$$x = a_0+\frac{1}{a_1 + \frac{1}{a_2+\frac{1}{a_3+...}}}$$
可以把连分数简记为:$x = [a_0;a_1, a_2, a_3...]$.
有理数的连分数有两种表示形式:
$$\frac{p}{q} = [a_0;a_1, a_2, a_3, ...,a_n,1] 或 [a_0;a_1, a_2, a_3, ..., a_n+1]$$
所有无限连分数都是无理数,而所有无理数都可以用一种精确的方式表示成无限连分数,可以用这种方法逼近,无理数的值。
三、关于一个非完全平方数的平方根的连分数表示
可以证明:一个非完全平方数的平方根是以周期性呈现的:
比如:
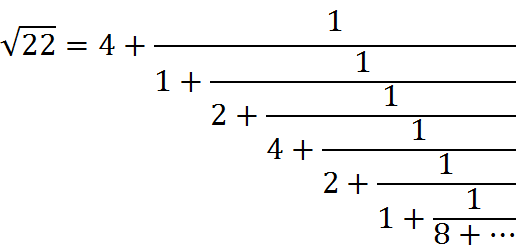
简写为:
$$\sqrt 22 = [4;1,2,4,2,1,8]$$
在之后就会循环出现1,2,4,2,1,8
我们不妨这样记这种连分数的形式:
$$\sqrt22 = [4;<1,2,4,2,1,8>]$$
显然循环节的长度是6
并且还有个重要的特点:这个循环节一定是 $a_1$ 开始,且最后一个数 $a_n$ 一定是 $a_0$ 的2倍。
五、且佩尔方程的最小特解:
我们将 $\sqrt D$ 写成连分数的形式:(相当于用连分数无线逼近平方根)
$$\sqrt D = [a_0;<a_1, a_2, ..., a_{n-1},2a_0>]$$
并且我们记:
$$\frac{p}{q} = [a_0; a_1, a_2, ..., a_{n-1}]$$
(关于计算p,q:只要按照连分数的展开形式,迭代计算即可)
其中如果记循环节长度为s
那么有如下结论:
1、如果s为偶数时。最小特解为:
$$x_0 = p, y_0 = q$$
2、如果s为奇数时,最小特解为:
$$x_0 = 2p^2+1, y_0 = 2pq$$
六、计算 $\sqrt D$ 的连分数
我们希望得到准确的连分数展开,那么关键在于不用浮点型计算。
接下来以 $\sqrt {22}$ 为例: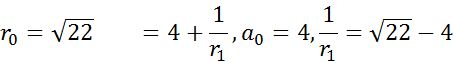

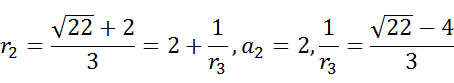
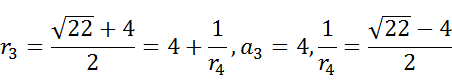
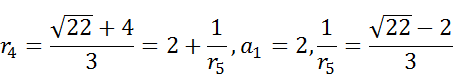

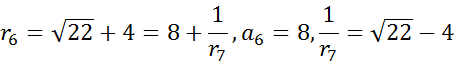
按照这种方式,我们计算出了的连分数:$\sqrt {22} = [4;<1,2,4,2,1,8>]$.
然后可以计算出来:
$$\frac{197}{42} = [4;1,2,4,2,1]$$
由于循环节长度6是偶数,那么佩尔方程 $x^2 -22y^2 = 1$ 的最小特解是:$x_0 = 197, y_0 = 42$.
之后我们参照上面的例子,很容易设计出计算连分数的算法。
代码
结果很大1000以内好多结果都超long long了。。。要改成大数才行。。。
#include<cstdio> #include<cstring> #include<cmath> #include<cstdlib> using namespace std; typedef long long ll; ll a[20000]; bool pell_minimum_solution(ll n,ll &x0,ll &y0){ ll m=(ll)sqrt((double)n); double sq=sqrt(n); int i=0; if(m*m==n)return false;//当n是完全平方数则佩尔方程无解 a[i++]=m; ll b=m,c=1; double tmp; do{ c=(n-b*b)/c; tmp=(sq+b)/c; a[i++]=(ll)(floor(tmp)); b=a[i-1]*c-b; //printf("%lld %lld %lld\n",a[i-1],b,c); }while(a[i-1]!=2*a[0]); ll p=1,q=0; for(int j=i-2;j>=0;j--){ ll t=p; p=q+p*a[j]; q=t; //printf("a[%d]=%lld %lld %lld\n",j,a[j],p,q); } if((i-1)%2==0){x0=p;y0=q;} else{x0=2*p*p+1;y0=2*p*q;} return true; } int main(){ ll n,x,y; while(~scanf("%lld",&n)){ if(pell_minimum_solution(n,x,y)){ printf("%lld^2-%lld*%lld^2=1\t",x,n,y); printf("%lld-%lld=1\n",x*x,n*y*y); } }
一个java打表的代码:

import java.io.*; import java.math.*; import java.util.*; public class main { static long [] a = new long [1000]; static BigInteger x; static BigInteger y; public static void main(String [] args) throws FileNotFoundException{ FileReader fin = new FileReader ("data.in"); File fout = new File("data.out"); PrintStream pw = new PrintStream(fout); Scanner cin = new Scanner(fin); System.setOut(pw); while(cin.hasNext()){ long n=cin.nextLong(); if(pell_solution(n)){ System.out.print("\""+x+"\","); }else{ System.out.print("\"no solution\","); } } } public static boolean pell_solution(long D){ double sq=Math.sqrt((double)D); long m=(long) Math.floor(sq); int i=0; if(m*m==D)return false; a[i++]=m; long b=m,c=1; double tmp; do{ c=(D-b*b)/c; tmp=(sq+b)/c; a[i++]=(long)(Math.floor(tmp)); b=a[i-1]*c-b; }while(a[i-1]!=2*a[0]); BigInteger p=new BigInteger("1"); BigInteger q=new BigInteger("0"); BigInteger t; for(int j=i-2;j>=0;j--){ t=p; p=q.add(p.multiply(BigInteger.valueOf(a[j]))); q=t; } if((i-1)%2==0){ x=p;y=q; }else{ x=BigInteger.valueOf(2).multiply(p).multiply(p).add(BigInteger.ONE); y=BigInteger.valueOf(2).multiply(p).multiply(q); } return true; } }
