以下题目均为口胡/看题解,并没写过代码,有错误请提出
A

B
显然如果一个区间是升序的,那把它排序没用
考虑两个区间\([x,x+k-1],[y,y+k-1](x<y)\)相交,把它们排序后只贡献一次的情况
有\(max(a[x]…a[y-1])< min(a[y]…a[x+k-1])\),\(max(a[y]…a[x+k-1])< min(a[x+k]…a[y+k-1])\),且\(a[x]…a[y-1]\),\(a[x+k]…a[y+k-1]\)单调递增
写这么大坨就是\(a[y-1]< min(a[y]…a[x+k-1])\),\(a[x+k]> max(a[y]…a[x+k-1])\)
处理出一个位置开始的最长上升/下降子串是\(O(n)\)的,求出来,然后以这个为基础,可以对每个\(y\)二分出最大的\(x+k-1\)的位置,注意到每个\(y\)只有最大的\(x+k-1\)是有用的,下面证明一下:
画个图,其中粉线为上升字串,绿线为区间中任取的一个合法的\(x+k-1\)的结果,黑线、蓝线分别为\([y,y+k-1]\),\([x_{max},x_{max}+k-1]\)
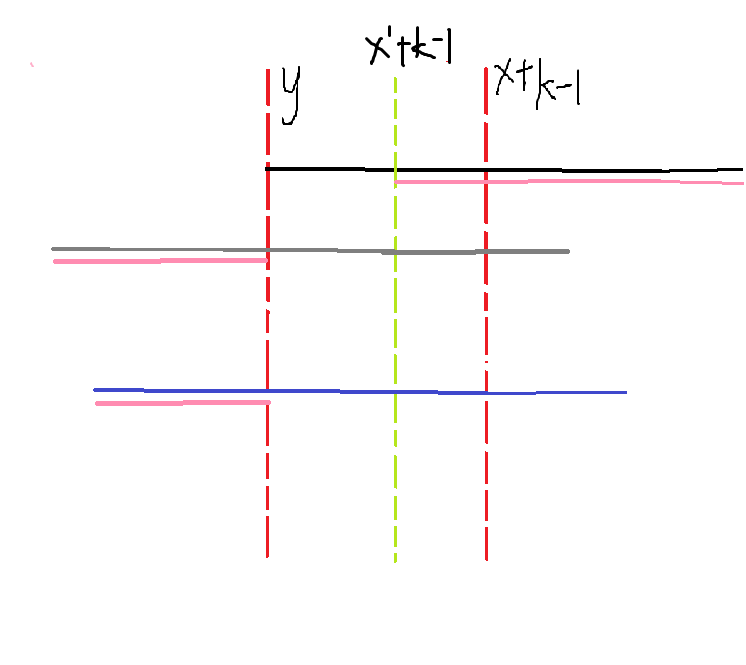
显然对于红绿之间的最小值\(\geq\)红红之间的最小值,所以\(a[y-1]\)的限制可以实现,又因为绿线是个合法的区间,所以\(a[x'+k-1]\)\(>\)红绿之间的最大值,又因为\([x'+k-1,x_{max}+k-1]\)被粉线覆盖,所以红线之间的最大值为\(a[x_{max}+k-1]\),显然\(a[x_{max}+k]>a[x_{max}+k-1]\),得证。
c
\(\sum\limits_{i=1}^n \sum\limits_{j=i+1}^nlcm(A_i,A_j)\\ =\frac{\sum\limits_{i=1}^n \sum\limits_{j=1}^n\frac{A_iA_j}{gcd(A_i,A_j)}-\sum A_i}{2}\\\)
设\(P=\sum\limits_{i=1}^n \sum\limits_{j=1}^n\frac{A_iA_j}{gcd(A_i,A_j)}\\ =\sum\limits_{d=1}^{mx} \frac{1}{d}\sum\limits_{x=1}^{mx/d}\mu(x)\sum\limits_{xd|A_i,xd|A_j}A_iA_j\\= \sum\limits_{T=1}^{mx} (\sum\limits_{d|T} \mu(T/d)/d)(\sum\limits_{T|A_i,T|A_j} A_iA_j)\)
这两坨东西都可以\(O(mxlnmx)\)预处理
D
开始不会了……看题解去了QAQ
显然当\(C\)全0时,把它连成一棵树是符合要求的
于是可以按提示把\(C=0\)的所有边连出一些连通块,且这些连通块都是树
此时如果条件给出同个连通块的两点中有多条路径是不合法的
设现在连通块个数为\(cnt\),现在还有\(m-(n-cnt)\)条边要连
题目限制是个连通图,所以如果没有\(C=1\)的边的话,还要连\([cnt-1,(cnt-1)cnt/2]\)条边让它联通
否则可以在连通块之间连个环出来,即连\(cnt\)条边,感受一下就知道这是下界,上界还是\((cnt-1)cnt/2\)需要注意的是\(c=2\)是连不出来的,因为一个连通块向另一个连通块连了两条边,创造了一条路径出来。