\(A\)
什么玩意儿……
const char c[]={"snuke"};
char s[15];int n,m;
int main(){
scanf("%d%d",&n,&m);
fp(i,1,n)fp(j,1,m){
scanf("%s",s);
bool flag=1;
fp(k,0,4)if(s[k]!=c[k]){flag=0;break;}
if(flag)return printf("%c%d\n",j-1+'A',i),0;
}
return 233;
}\(B\)
什么玩意儿……
int n,sum,res,c;
int main(){
scanf("%d",&n);
while(sum<n)++res,sum+=res;
fp(i,1,res)if(i!=sum-n)printf("%d\n",i);
return 0;
}\(C\)
把每种语言作为一个点,向所有会这个语言的人连边,最后判断是否所有人都在同一连通块中即可
//quming
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
const int N=5e5+5;
int fa[N],n,m;
inline int find(R int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
int main(){
scanf("%d%d",&n,&m);
fp(i,1,n+m)fa[i]=i;
for(R int i=1,k,x;i<=n;++i){
scanf("%d",&k);
while(k--)scanf("%d",&x),fa[find(i)]=find(x+n);
}
fp(i,1,n)if(find(i)!=find(1))return puts("NO"),0;
puts("YES");
return 0;
}\(D\)
首先肯定是尽量多匹配\(m\)的倍数,那么把所有数都放到模\(m\)意义下,对于\(i\)会有影响的只有\(m-i\),那么肯定是把\(m\)的倍数的匹配完,剩下的全都用来匹配相同的就是了
记得特判一下\(m/2\)和\(0\),因为它们要匹配\(m\)的倍数的话只能和自己
//quming
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
const int N=5e5+5;
int cnt[N],c[N],sum[N],n,m,res;
int main(){
scanf("%d%d",&n,&m);
for(R int i=1,x;i<=n;++i)scanf("%d",&x),++c[x],++cnt[x%m];
fp(i,1,1e5)sum[i%m]+=c[i]>>1;
for(R int i=1,x;i<m-i;++i){
x=min(cnt[i],cnt[m-i]);
res+=x,cnt[i]-=x,cnt[m-i]-=x;
}
if(m&1^1)res+=cnt[m>>1]>>1,cnt[m>>1]&=1;
if(cnt[0])res+=cnt[0]>>1,cnt[0]&=1;
fp(i,0,m-1)res+=min(sum[i],cnt[i]>>1);
printf("%d\n",res);
return 0;
}\(E\)
我好像想的太复杂了……
首先吃小饼干的次数绝对不会超过\(O(\log n)\),那么我们干脆枚举一下吃了多少次小饼干
假设当前吃了\(i\)次小饼干,那么假设出去吃饼干之外剩下的部分花了时间\(t\),那么对于这\(t\)的时间肯定是平均分配最优的
我们二分出最小的\(t\)满足吃了\(i\)次小饼干的情况下使得最终剩余的饼干个数大于等于\(n\),那么用\(t+i\tmes A\)更新答案就是了
//quming
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
typedef long long ll;
ll n,a,res,l,r,mid,ans,w;
inline ll calc(R ll x,R ll y){
R ll res=1;
fp(i,1,x%y){
res*=x/y+1;
if(res>1e14)return 1e18;
}
fp(i,1,y-x%y){
res*=x/y;
if(res>1e14)return 1e18;
}
return res;
}
int main(){
scanf("%lld%lld",&n,&a),res=n;
fp(i,1,40){
l=1,r=2e6,ans=0;
while(l<=r){
mid=(l+r)>>1,w=calc(mid,i+1);
w>=n?(ans=mid,r=mid-1):l=mid+1;
}
cmin(res,ans+i*a);
}
printf("%lld\n",res);
return 0;
}\(F\)
\(dp\)还是不过关啊……数数能力还是不够……
首先我们发现,这条长度为\(m\)的路径强联通当且仅当
\(1.\)所有点都在这条路径中出现
\(2.\)路径的最后一个点能到达\(1\)号点
必要性和充分性都比较容易证明
那么我们记\(f[i][j][k]\)表示现在已经连了\(i\)条边,其中涉及了\(j\)个点,且\(1\)所在的强联通分量中点数为\(k\),那么只要枚举新的一步是走到未走过的点,已经走过但不在强联通分量中的点,还是在强联通分量中的点三种情况就好了
//quming
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
const int P=1e9+7;
inline void upd(R int &x,R int y){(x+=y)>=P?x-=P:0;}
inline int add(R int x,R int y){return x+y>=P?x+y-P:x+y;}
inline int dec(R int x,R int y){return x-y<0?x-y+P:x-y;}
inline int mul(R int x,R int y){return 1ll*x*y-1ll*x*y/P*P;}
int ksm(R int x,R int y){
R int res=1;
for(;y;y>>=1,x=mul(x,x))(y&1)?res=mul(res,x):0;
return res;
}
const int N=305;
int f[N][N][N],n,m;
int main(){
scanf("%d%d",&n,&m);
f[0][1][1]=1;
fp(i,0,m-1)fp(j,1,min(n,i+1))fp(k,1,j)if(f[i][j][k]){
upd(f[i+1][j+1][k],mul(f[i][j][k],n-j));
upd(f[i+1][j][k],mul(f[i][j][k],j-k));
upd(f[i+1][j][j],mul(f[i][j][k],k));
}
printf("%d\n",f[m][n][n]);
return 0;
}\(G\)
发现杏子的能力还是不够啊……
首先,根据\(kruskal\)的过程,对于两条边\((u,v,w)\)和\((a,b,c)\),如果\(w<c\),那么在考虑到后面一条边的时候\(u,v\)必定已经在一个连通块中了
其次,根据\(prim\)的过程,对于一个还不在当前连通块中的点,我们关心的只有这个点到这个连通块的最小距离,甚至都不关心它到底和这个连通块中哪一个点相连
这样的话,对于需要连的边\((a,b,w_1)\)和\((b,a+1,w_2)\),其中\(w_1<w_2\),我们完全可以把第二条边变成\((a,a+1,w_2)\)且不影响最小生成树的权值
这样的话,最终可以把所有的边都连成\((u,u+1,w)\)的形式,只要对于这一圈环,每一条边都找到最小的就好了
//quming
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
typedef long long ll;
const int N=5e5+5;
struct eg{
int u,v,w;
inline bool operator <(const eg &b)const{return w<b.w;}
}E[N];
int fa[N],f[N],n,q,tot;ll res;
inline int find(R int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
int main(){
scanf("%d%d",&n,&q);
fp(i,0,n-1)f[i]=0x3f3f3f3f;
for(R int i=1,u,v,w;i<=q;++i){
scanf("%d%d%d",&u,&v,&w);
E[++tot]={u,v,w},cmin(f[u],w+1),cmin(f[v],w+2);
}
fp(i,1,n-1)cmin(f[i],f[i-1]+2);
cmin(f[0],f[n-1]+2);fp(i,1,n-1)cmin(f[i],f[i-1]+2);
fp(i,0,n-2)E[++tot]={i,i+1,f[i]};E[++tot]={n-1,0,f[n-1]};
fp(i,0,n-1)fa[i]=i;
sort(E+1,E+1+tot);
for(R int i=1,u,v;i<=tot;++i){
u=find(E[i].u),v=find(E[i].v);
if(u!=v)res+=E[i].w,fa[u]=v;
}
printf("%lld\n",res);
return 0;
}\(H\)
前面都好说,最神仙的一步是真的推不出来啊……
ps:这一篇基本上是题解的翻译
首先我们不难发现一个性质,就是如果一个人在\(i\),另一个人在\(j\),且\(i<j\),那么在\(i\)的那个人肯定是把\(i\)一直移到\(j-1\),再考虑之后的情况,这是最优的
那么我们设\(f[i]\)表示后手在\(i\),先手在\(i-1\),且只考虑\([i+1,n]\)的数字上的贡献,此时先手减后手得分的最大值,那么容易推出转移方程(设\(sum_i\)表示\(a_i\)的前缀和)
\[ \begin{aligned} f_i=\max_{j=i+1}^n{a_j-(sum_{j-1}-sum_i)-f_j} \end{aligned} \]
初值为\(f_n=0\),那么最终的答案就是\(f_2+a_1-a_2\)了
然而这个东西如果直接算的话是\(O(n^2)\)的,连部分分都过不了
考虑优化,我们考虑对于\(f_i\)和\(f_{i+1}\),它们的柿子有什么区别
\[ \begin{aligned} &f_i=\max_{j=i+1}^n{a_j-(sum_{j-1}-sum_i)-f_j}\\ &f_{i+1}=\max_{j=i+2}^n{a_j-(sum_{j-1}-sum_{i+1})-f_j}\\ &f_i=\max(f_{i+1}-a_{i+1},a_{i+1}-f_{i+1})\\ \end{aligned} \]
我们发现可以化成最后一行那个样子!这样的话一次转移记就是\(O(n)\)的了!可以过部分分了
这个故事告诉我们颓柿子的时候最好不要把区间和写成前缀和相减的形式不然什么杏子都看不出来
继续考虑,柿子可以变成\(f_i=|f_{i+1}-a_{i+1}|\),那么就可以写出一个暴力的代码
inline int calc(){
R int res=a[n];
fd(i,n-1,3)res=abs(res-a[i]);
return res+a[1]-a[2];
}继续考虑,发现这里\(\sum a_i\leq 10^6\)很奇怪啊……一看就有阴谋……
记\(sum=\sum_{i=3}^{n-1}a_i\),我们发现对于这个柿子,当\(a_n\geq sum\)的时候显然最终的\(res\)就是\(a[n]-sum\),那么我们接下来就只需要考虑\(a[n]\leq sum\)的情况了
我们记\(dp[i][j]\)表示处理完\(|f_i-a_i|\)之后此时的值为\(j\),做完接下来所有操作之后的值是多少
初值为\(dp[3][i]=i\),然后我们要倒推出\(dp[n][i]\),那么最终的答案就是\(dp[n][a[n]]\)
首先,不难发现\(dp[i+1][j]=dp[i][|j-a[i]|]\)
我们先来打一个表(盗用题解里的图),以\(n=6,a[3]=5,a[4]=3,a[5]=4\)为例
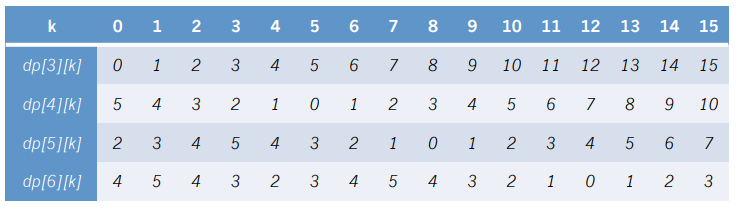

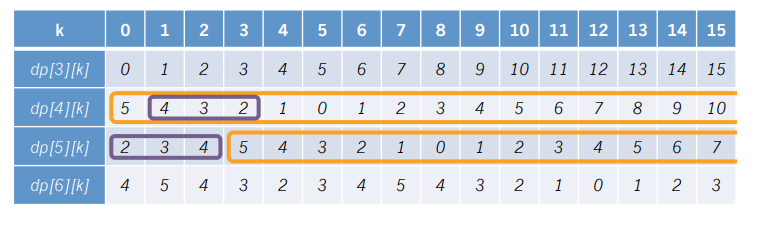
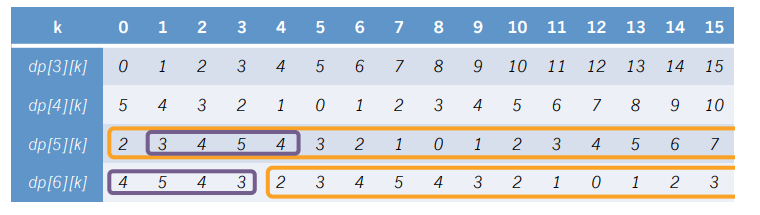
我们惊讶的发现,从\(dp[i]\)到\(dp[i+1]\)的过程,就是把\(dp[i]\)中所有数右移\(a[i]\)位,并将\(dp[i][1...a[i]]\)取反之后作为\(dp[i+1][0...a[i]-1]\)!!!
这样的话,如果我们用双端队列,可以做到单次转移复杂度\(O(a_i)\),总的复杂度不会超过\(O(sum)\)
然后就没有然后了
代码并不难打
//quming
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
const int N=2e6+5;
int f[N],a[N],cnt[N],q[N],to[N],sum,h,t,n,m;
int main(){
// freopen("testdata.in","r",stdin);
scanf("%d",&n);
fp(i,1,n-1)scanf("%d",&a[i]);
scanf("%d",&m);
fp(i,3,n-1)sum+=a[i];
h=1e6+5,t=h-1;
fp(i,0,1e6)q[++t]=i;
fp(i,3,n-1)for(R int j=h+1,s=h+a[i];j<=s;++j)q[--h]=q[j];
fp(i,h,h+1e6)to[i-h]=q[i];
while(m--){
scanf("%d",&a[n]);
printf("%d\n",(a[n]>=sum?a[n]-sum:to[a[n]])+a[1]-a[2]);
}
return 0;
}\(I\)
越来越感觉自己的思维能力无限接近于\(0\)……
首先,如果行数为奇数的话,那么中间那一行是不会被列的翻转影响的,所以如果这一行自己反转之后会变得不一样,我们可以直接把答案乘\(2\),之后就不用再考虑这一行了,对于列同理
那么现在行和列都是偶数,我们可以把整个格子如下平均分成四部分并标号,标号的原则是每一个格子和它经过若干次翻转操作之后能到达的格子标号相同。我们把标号相同的记为一个组
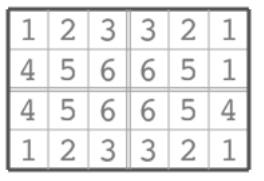
首先,手玩一下不难发现我们可以单独对于一个组进行变换而不影响其他格子,且如果把原来的格子的顺序依次记为\(1,2,3,4\),即一个排列,那么一次变换等价于对格子进行一次置换,且置换之后的排列必定是一个偶排列(偶排列即对原排列进行偶数次\(swap\)),所以方案数是\({4!\over 2}=12\)
再考虑更深的情况之前我们先排除一种特殊情形,即这四个格子中有相同元素的情况,因为上面那种情况等价于对格子进行偶数次\(swap\),那么我们可以通过相邻元素间的\(swap\)来消耗次数,这样的话最终不管是奇排列还是偶排列都可以形成
回来考虑,对于某一组,当且仅当这一组所在的所有位置的某一行或某一列被\(reverse\)之后,这一组才可以搞出奇排列,且只能搞出奇排列
那么我们建出一张二分图,左边的点代表行,右边的点代表列,对于每一个不是特殊情况的组,从对应的行向对应的列连边,然后对于每一个点选择一个值\(0/1\)(表示该行/列反不反转),并将每条边的权值设为它所连接的两个点之和,这样如果这条边的权值是奇数就代表这组是奇排列,否则是偶排列。那么只要知道所有边的方案不同的可能是多少
首先对于一个联通快,只要确定了其中一个生成树上每条边的权值,其它每一条边都是可以依次确定的
那么一个大小为\(i\)的连通块的方案就是\(2^{i-1}\)了
然后没有然后了
//quming
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
const int P=1e9+7;
inline void upd(R int &x,R int y){(x+=y)>=P?x-=P:0;}
inline int add(R int x,R int y){return x+y>=P?x+y-P:x+y;}
inline int dec(R int x,R int y){return x-y<0?x-y+P:x-y;}
inline int mul(R int x,R int y){return 1ll*x*y-1ll*x*y/P*P;}
int ksm(R int x,R int y){
R int res=1;
for(;y;y>>=1,x=mul(x,x))(y&1)?res=mul(res,x):0;
return res;
}
const int N=505;
char s[N][N];int fa[N],sz[N],bin[N],n,m,res;
inline int find(R int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
void ck(){
if(n&1){
R int c=(n+1)>>1,fl=1;
fp(j,1,m)if(s[c][j]!=s[c][m-j+1]){fl=0;break;}
if(!fl)res*=2;
}
if(m&1){
R int r=(m+1)>>1,fl=1;
fp(i,1,n)if(s[i][r]!=s[n-i+1][r]){fl=0;break;}
if(!fl)res*=2;
}
}
int fac[15],st[15],top;
bool ck(R int i,R int j){
top=0;
st[++top]=s[i][j];
st[++top]=s[n-i+1][j];
st[++top]=s[i][m-j+1];
st[++top]=s[n-i+1][m-j+1];
sort(st+1,st+1+top);
R int sum=1;
for(R int l=1,r=1;l<=top;l=r){
while(r<=top&&st[r]==st[l])++r;
sum*=fac[r-l];
}
sum=24/sum,res=mul(res,sum==24?12:sum);
return sum==24;
}
int main(){
// freopen("testdata.in","r",stdin);
scanf("%d%d",&n,&m),res=1;
fp(i,1,n)scanf("%s",s[i]+1);
ck();
fp(i,1,(n>>1)+(m>>1))fa[i]=i,sz[i]=1;
bin[0]=1;fp(i,1,(n>>1)+(m>>1))bin[i]=mul(bin[i-1],2);
fac[0]=1;fp(i,1,4)fac[i]=fac[i-1]*i;
fp(i,1,n>>1)fp(j,1,m>>1)
if(ck(i,j)){
R int u=find(i),v=find((n>>1)+j);
if(u!=v)fa[u]=v,sz[v]+=sz[u];
}
fp(i,1,(n>>1)+(m>>1))if(find(i)==i)res=mul(res,bin[sz[i]-1]);
printf("%d\n",res);
return 0;
}\(J\)
最后一题放弃了……