一个求平方根方法

昨天在论坛上看到一个算法，是算平方根的，很是惊艳，颇有艺术性。

公式：

　　　　(X1  + n/X1 )/2 = X2

n为要算的值，x1一开始随便取个值，然后算出x2，然后不断的把x2带入x1，算出x3，以此类推，大概迭代几次就很逼近要算的平方根了。

如：要算  7659的平方根

x1取10

x2 近似等于 388

x3 近似等于204 

x4 近似 92 

x5近似 87.6

扫描二维码关注公众号，回复： 7250148 查看本文章

x6近似 87.5157

87.5157^2 =7658.99775

迭代5次以后，取值范围已经很接近了，其他随便举例子基本上也都是五次左右就很接近了。

这么牛逼的算法是谁提出的呢？哪个大公司的大牛？这种老艺术家肯定年薪千万了吧。。

查了下资料，果然不出所望，这个公式是牛顿（对，头上落了个苹果的老艺术，真正的大牛，大牛鼻祖的牛）提出的牛顿迭代法求平方根。

这个算法的知识用到了我们高中数学学过的线性方程和导数方程。

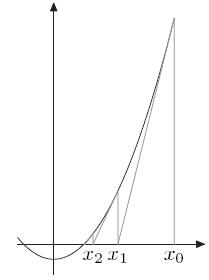
已知n，求x的解 :   x² = n

f(x) = x² -n    令 f(x) = 0，也就是求曲线与x轴相交时，x的值

   首先取x₀，如果x₀不是解，做一个经过(x₀,f(x₀))这个点的切线，与x轴的交点为x₁。

   同样的道理，如果x₁不是解，做一个经过(x₁,f(x₁))这个点的切线，与x轴的交点为x₂。

   以此类推。

   以这样的方式得到的x_i会无限趋近于f(x)=0的解。

过(x_i, f(x_i))这个点的切线方程为f(x) = f(x_i) + f’(x_i)(x - x_i)，其中f'(x)为f(x)的导数, 也就是切线斜率，求证方法在下面，本题中斜率为2x。

令切线方程等于0，即可求出x_i+1=x_i - f(x_i) / f'(x_i)。

一顿数学运算简化后：x_i+1=x_i - (x_i² - n) / (2x_i) = x_i - x_i / 2 + n / (2x_i) = x_i / 2 + n / 2x_i = (x_i + n/x_i) / 2

这个算法可以运用在编程中，具体不写了，数值稍微修改也可以求多次幂或者其他曲线函数的根。

幂函数导数公式的证明：

y=x^a

两边取对数lny=alnx

两边对x求导(1/y)*y'=a/x

所以y'=ay/x=ax^a/x=ax^(a-1)

这里，y'=2x

原理可参考，通俗易懂：https://blog.csdn.net/ccnt_2012/article/details/81837154