本文主要内容摘自下面文献:
Urkowitz (1967)一文中,分别讨论了低通和带通两种情况。这里主要集中讨论带通情况。设发送的低通信号为
S
L
P
(
t
)
=
s
c
(
t
)
+
j
s
s
(
t
)
S_{\rm LP}(t)=s_c(t)+js_s(t)
S L P ( t ) = s c ( t ) + j s s ( t )
h
=
α
e
j
θ
h=\alpha e^{j\theta}
h = α e j θ
r
(
t
)
=
{
R
{
[
h
s
L
P
(
t
)
+
n
L
P
(
t
)
]
e
j
2
π
f
c
t
}
:
H
1
R
{
n
L
P
(
t
)
e
j
2
π
f
c
t
}
:
H
0
r(t)={\Large\{ }\begin{aligned} {\mathcal R}\{[hs_{\rm LP}(t)+n_{\rm LP}(t)]e^{j2\pi f_ct}\}:H_1\\ {\mathcal R}\{n_{\rm LP}(t)e^{j2\pi f_ct}\}:H_0 \end{aligned}
r ( t ) = { R { [ h s L P ( t ) + n L P ( t ) ] e j 2 π f c t } : H 1 R { n L P ( t ) e j 2 π f c t } : H 0
γ
=
α
2
E
s
N
0
\gamma =\frac{\alpha^2 E_s}{N_0}
γ = N 0 α 2 E s
r
=
2
N
0
∫
0
T
r
2
(
t
)
d
t
.
r=\frac{2}{N_0}\int_{0}^{T}r^2(t)dt.
r = N 0 2 ∫ 0 T r 2 ( t ) d t .
H
0
H_0
H 0
H
1
H_1
H 1
H
0
H_0
H 0
n
(
t
)
=
n
c
(
t
)
cos
(
2
π
f
c
t
)
−
n
s
(
t
)
sin
(
2
π
f
c
t
)
,
n(t)=n_c(t)\cos(2\pi f_ct)-n_s(t)\sin(2\pi f_ct),
n ( t ) = n c ( t ) cos ( 2 π f c t ) − n s ( t ) sin ( 2 π f c t ) ,
r
=
2
N
0
∫
0
T
n
2
(
t
)
d
t
=
1
N
0
∫
0
T
[
n
c
2
(
t
)
+
n
s
2
(
t
)
]
d
t
\begin{aligned} r&=\frac{2}{N_0}\int_{0}^{T}n^2(t)dt\\ &=\frac{1}{N_0}\int_{0}^{T}\left[ n_c^2(t)+n_s^2(t)\right]dt\\ \end{aligned}
r = N 0 2 ∫ 0 T n 2 ( t ) d t = N 0 1 ∫ 0 T [ n c 2 ( t ) + n s 2 ( t ) ] d t
n
c
(
t
)
n_c(t)
n c ( t )
n
s
(
t
)
n_s(t)
n s ( t )
W
W
W
2
W
2W
2 W
N
=
2
W
T
N=2WT
N = 2 W T
n
c
(
t
)
=
∑
i
=
1
N
/
2
n
c
i
s
i
n
c
(
W
t
−
i
)
n
s
(
t
)
=
∑
i
=
1
N
/
2
n
s
i
s
i
n
c
(
W
t
−
i
)
,
\begin{aligned} n_c(t)&=\sum_{i=1}^{N/2}n_{ci}{\rm sinc}\left(Wt-i \right)\\ n_s(t)&=\sum_{i=1}^{N/2}n_{si}{\rm sinc}\left(Wt-i \right), \end{aligned}
n c ( t ) n s ( t ) = i = 1 ∑ N / 2 n c i s i n c ( W t − i ) = i = 1 ∑ N / 2 n s i s i n c ( W t − i ) ,
r
=
1
N
0
W
∑
i
=
1
N
/
2
[
n
c
i
2
+
n
s
i
2
]
=
∑
i
=
1
N
/
2
[
(
n
c
i
N
0
W
)
2
+
(
n
s
i
N
0
W
)
2
]
r=\frac{1}{N_0W}\sum_{i=1}^{N/2}\left[ n_{ci}^2+n_{si}^2\right]=\sum_{i=1}^{N/2}\left[ \left(\frac{n_{ci}}{\sqrt{N_0W}}\right)^2+\left(\frac{n_{si}}{\sqrt{N_0W}}\right)^2\right]
r = N 0 W 1 i = 1 ∑ N / 2 [ n c i 2 + n s i 2 ] = i = 1 ∑ N / 2 [ ( N 0 W
n c i ) 2 + ( N 0 W
n s i ) 2 ]
χ
2
\chi^2
χ 2
2
T
W
2TW
2 T W
H
1
H_1
H 1
s
L
P
(
t
)
=
s
c
(
t
)
+
j
s
s
(
t
)
,
s_{\rm LP}(t)=s_c(t)+js_s(t),
s L P ( t ) = s c ( t ) + j s s ( t ) ,
h
L
P
=
α
c
+
j
α
s
h_{\rm LP}=\alpha_c+j\alpha_s
h L P = α c + j α s
s
L
P
′
(
t
)
=
α
c
s
c
(
t
)
+
j
α
c
s
s
(
t
)
+
j
α
s
s
c
(
t
)
−
α
s
s
s
(
t
)
,
s'_{\rm LP}(t)=\alpha_cs_c(t)+j\alpha_c s_s(t)+j\alpha_s s_c(t)-\alpha_ss_s(t),
s L P ′ ( t ) = α c s c ( t ) + j α c s s ( t ) + j α s s c ( t ) − α s s s ( t ) ,
s
′
(
t
)
=
R
[
s
L
P
′
(
t
)
e
j
2
π
f
c
t
]
=
[
α
c
s
c
(
t
)
−
α
s
s
s
(
t
)
]
cos
(
2
π
f
c
t
)
−
[
α
c
s
s
(
t
)
+
α
s
s
c
(
t
)
]
sin
(
2
π
f
c
t
)
\begin{aligned} s'(t)&={\mathcal R}\left[ s'_{\rm LP}(t)e^{j2\pi f_ct} \right]\\ &=\left[ \alpha_cs_c(t)-\alpha_ss_s(t)\right]\cos(2\pi f_ct)-\left[\alpha_c s_s(t)+\alpha_s s_c(t)\right]\sin(2\pi f_ct)\\ \end{aligned}
s ′ ( t ) = R [ s L P ′ ( t ) e j 2 π f c t ] = [ α c s c ( t ) − α s s s ( t ) ] cos ( 2 π f c t ) − [ α c s s ( t ) + α s s c ( t ) ] sin ( 2 π f c t )
r
(
t
)
=
[
α
c
s
c
(
t
)
−
α
s
s
s
(
t
)
+
n
c
(
t
)
]
cos
(
2
π
f
c
t
)
−
[
α
c
s
s
(
t
)
+
α
s
s
c
(
t
)
+
n
s
(
t
)
]
sin
(
2
π
f
c
t
)
=
r
c
(
t
)
cos
(
2
π
f
c
t
)
−
r
s
(
t
)
sin
(
2
π
f
c
t
)
\begin{aligned} r(t)&=\left[ \alpha_cs_c(t)-\alpha_ss_s(t)+n_c(t)\right]\cos(2\pi f_ct)-\left[\alpha_c s_s(t)+\alpha_s s_c(t)+n_s(t)\right]\sin(2\pi f_ct)\\ &=r_c(t)\cos(2\pi f_ct)-r_s(t)\sin(2\pi f_ct) \end{aligned}
r ( t ) = [ α c s c ( t ) − α s s s ( t ) + n c ( t ) ] cos ( 2 π f c t ) − [ α c s s ( t ) + α s s c ( t ) + n s ( t ) ] sin ( 2 π f c t ) = r c ( t ) cos ( 2 π f c t ) − r s ( t ) sin ( 2 π f c t )
r
c
(
t
)
=
∑
i
=
1
N
/
2
[
α
c
s
c
i
−
α
s
s
s
i
+
n
c
i
]
s
i
n
c
(
W
t
−
i
)
r
s
(
t
)
=
∑
i
=
1
N
/
2
[
α
c
s
s
i
+
α
s
s
c
i
+
n
s
i
]
s
i
n
c
(
W
t
−
i
)
,
\begin{aligned} r_c(t)&=\sum_{i=1}^{N/2}[\alpha_c s_{ci}-\alpha_s s_{si}+n_{ci}]{\rm sinc}\left(Wt-i \right)\\ r_s(t)&=\sum_{i=1}^{N/2}[\alpha_c s_{si}+\alpha_s s_{ci}+n_{si}]{\rm sinc}\left(Wt-i \right), \end{aligned}
r c ( t ) r s ( t ) = i = 1 ∑ N / 2 [ α c s c i − α s s s i + n c i ] s i n c ( W t − i ) = i = 1 ∑ N / 2 [ α c s s i + α s s c i + n s i ] s i n c ( W t − i ) ,
(2)
r
=
2
N
0
∫
0
T
r
2
(
t
)
d
t
=
1
N
0
∫
0
T
[
r
c
2
(
t
)
+
r
s
2
(
t
)
]
d
t
,
\tag{2} \begin{aligned} r=&\frac{2}{N_0}\int_{0}^{T}r^2(t)dt\\ &=\frac{1}{N_0}\int_{0}^{T}\left[ r_c^{2}(t)+r_s^{2}(t)\right]dt\\ \end{aligned},
r = N 0 2 ∫ 0 T r 2 ( t ) d t = N 0 1 ∫ 0 T [ r c 2 ( t ) + r s 2 ( t ) ] d t , ( 2 )
H
1
:
r
=
1
N
0
W
[
∑
i
=
1
N
/
2
(
α
c
s
c
i
−
α
s
s
s
i
+
n
c
i
)
2
+
∑
i
=
1
N
/
2
(
α
c
s
s
i
+
α
s
s
c
i
+
n
s
i
)
2
]
=
∑
i
=
1
N
/
2
(
α
c
s
c
i
−
α
s
s
s
i
+
n
c
i
N
0
W
)
2
+
∑
i
=
1
N
/
2
(
α
c
s
s
i
+
α
s
s
c
i
+
n
s
i
N
0
W
)
2
\begin{aligned} H_1:\qquad r&=\frac{1}{N_0W}\left[ \sum_{i=1}^{N/2}(\alpha_c s_{ci}-\alpha_s s_{si}+n_{ci})^2+\sum_{i=1}^{N/2}(\alpha_c s_{si}+\alpha_s s_{ci}+n_{si})^2\right]\\ &=\sum_{i=1}^{N/2}\left(\frac{\alpha_c s_{ci}-\alpha_s s_{si}+n_{ci}}{\sqrt{N_0W}}\right)^2+\sum_{i=1}^{N/2}\left(\frac{\alpha_c s_{si}+\alpha_s s_{ci}+n_{si}}{\sqrt{N_0W}}\right)^2 \end{aligned}
H 1 : r = N 0 W 1 ⎣ ⎡ i = 1 ∑ N / 2 ( α c s c i − α s s s i + n c i ) 2 + i = 1 ∑ N / 2 ( α c s s i + α s s c i + n s i ) 2 ⎦ ⎤ = i = 1 ∑ N / 2 ( N 0 W
α c s c i − α s s s i + n c i ) 2 + i = 1 ∑ N / 2 ( N 0 W
α c s s i + α s s c i + n s i ) 2
χ
2
\chi^2
χ 2
σ
2
=
1
\sigma^2=1
σ 2 = 1
μ
=
2
γ
\mu=2\gamma
μ = 2 γ
γ
=
α
E
s
N
0
\gamma=\frac{\alpha E_s}{N_0}
γ = N 0 α E s
我们来推导下非中心参数:
μ
=
∑
i
=
1
N
/
2
(
α
c
2
s
c
i
2
N
0
W
+
α
s
2
s
s
i
2
N
0
W
)
+
∑
i
=
1
N
/
2
(
α
c
2
s
s
i
2
N
0
W
+
α
s
2
s
c
i
2
N
0
W
)
=
α
c
2
N
0
∑
i
=
1
N
/
2
s
c
i
2
W
+
α
s
2
N
0
∑
i
=
1
N
/
2
s
s
i
2
W
+
α
c
2
N
0
∑
i
=
1
N
/
2
s
s
i
2
W
+
α
s
2
N
0
∑
i
=
1
N
/
2
s
c
i
2
W
=
2
α
2
E
s
N
0
\begin{aligned} \mu&=\sum_{i=1}^{N/2}\left(\frac{\alpha_c^2 s^2_{ci}}{{N_0W}}+\frac{\alpha_s^2 s^2_{si}}{{N_0W}}\right)+\sum_{i=1}^{N/2}\left(\frac{\alpha_c^2 s^2_{si}}{{N_0W}}+\frac{\alpha_s^2 s^2_{ci}}{{N_0W}}\right)\\ &=\frac{\alpha_c^2}{N_0} \sum_{i=1}^{N/2}\frac{s^2_{ci}}{{W}}+\frac{\alpha_s^2}{N_0} \sum_{i=1}^{N/2}\frac{s^2_{si}}{{W}}+\frac{\alpha_c^2}{N_0} \sum_{i=1}^{N/2}\frac{s^2_{si}}{{W}}+\frac{\alpha_s^2}{N_0} \sum_{i=1}^{N/2}\frac{s^2_{ci}}{{W}}\\ &=\frac{2\alpha^2 E_s}{N_0} \end{aligned}
μ = i = 1 ∑ N / 2 ( N 0 W α c 2 s c i 2 + N 0 W α s 2 s s i 2 ) + i = 1 ∑ N / 2 ( N 0 W α c 2 s s i 2 + N 0 W α s 2 s c i 2 ) = N 0 α c 2 i = 1 ∑ N / 2 W s c i 2 + N 0 α s 2 i = 1 ∑ N / 2 W s s i 2 + N 0 α c 2 i = 1 ∑ N / 2 W s s i 2 + N 0 α s 2 i = 1 ∑ N / 2 W s c i 2 = N 0 2 α 2 E s
因此,
r
r
r
f
R
(
r
)
=
{
r
N
2
−
1
e
−
r
2
σ
2
σ
N
2
N
2
Γ
(
N
2
)
,
H
0
1
2
σ
2
(
r
μ
)
N
−
2
4
e
−
μ
+
r
2
σ
2
I
N
2
−
1
(
μ
r
σ
2
)
,
H
1
,
f_R(r)=\left\{\begin{aligned} \frac{r^{\frac{N}{2}-1}e^{-\frac{r}{2\sigma^2}}}{\sigma^N2^{\frac{N}{2}}\Gamma(\frac{N}{2})},&\quad H_0\\ \frac{1}{2\sigma^2}(\frac{r}{\mu})^{\frac{N-2}{4}}e^{-\frac{\mu+r}{2\sigma^2}}I_{\frac{N}{2}-1}(\frac{\sqrt{\mu r}}{\sigma^2}),&\quad H_1, \end{aligned}\right.
f R ( r ) = ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ σ N 2 2 N Γ ( 2 N ) r 2 N − 1 e − 2 σ 2 r , 2 σ 2 1 ( μ r ) 4 N − 2 e − 2 σ 2 μ + r I 2 N − 1 ( σ 2 μ r
) , H 0 H 1 ,
I
v
(
⋅
)
I_v(\cdot)
I v ( ⋅ )
v
v
v
为了计算检测与虚警概率,有很多近似方法。下面我们主要讨论高斯分布来近似。我们知道,随着样本数
N
N
N
y
y
y
r
r
r
r
∼
{
χ
N
2
,
H
0
χ
N
2
(
μ
)
,
H
1
r\sim \left\{\begin{aligned} \chi_N^2,&\quad H_0\\ \chi_N^2(\mu),&\quad H_1 \end{aligned} \right.
r ∼ { χ N 2 , χ N 2 ( μ ) , H 0 H 1
μ
=
2
E
s
α
2
N
0
=
2
γ
\mu=\frac{2E_s\alpha^2}{N_0}=2\gamma
μ = N 0 2 E s α 2 = 2 γ
γ
\gamma
γ
用高斯分布近似卡方分布:
m
=
∑
i
=
1
N
r
i
2
m=\sum_{i=1}^{N}r_i^2
m = ∑ i = 1 N r i 2
r
i
∼
N
(
0
,
σ
2
)
r_i\sim {\mathcal N}(0,\sigma^2)
r i ∼ N ( 0 , σ 2 )
m
σ
2
\frac{m}{\sigma^2}
σ 2 m
N
N
N
N
N
N
(
r
i
σ
2
)
2
(\frac{r_i}{\sigma^2})^2
( σ 2 r i ) 2
r
i
r_i
r i
σ
2
\sigma^2
σ 2
2
σ
4
2\sigma^4
2 σ 4
m
∼
N
(
N
σ
2
,
2
N
σ
4
)
.
m\sim {\mathcal N}(N\sigma^2,2N\sigma^4).
m ∼ N ( N σ 2 , 2 N σ 4 ) .
m
=
∑
i
=
1
N
r
i
2
m=\sum_{i=1}^{N}r_i^2
m = ∑ i = 1 N r i 2
r
i
∼
N
(
s
,
σ
2
)
r_i\sim {\mathcal N}(s,\sigma^2)
r i ∼ N ( s , σ 2 )
m
σ
2
\frac{m}{\sigma^2}
σ 2 m
N
N
N
N
s
+
N
Ns+N
N s + N
2
(
N
+
2
N
s
2(N+2Ns
2 ( N + 2 N s
N
s
=
μ
Ns=\mu
N s = μ
N
N
N
r
i
r_i
r i
N
(
1
+
s
)
σ
2
=
(
N
+
μ
)
σ
2
N(1+s)\sigma^2=(N+\mu)\sigma^2
N ( 1 + s ) σ 2 = ( N + μ ) σ 2
2
N
(
1
+
2
s
)
σ
4
=
2
(
N
+
2
μ
)
σ
4
2N(1+2s)\sigma^4=2(N+2\mu)\sigma^4
2 N ( 1 + 2 s ) σ 4 = 2 ( N + 2 μ ) σ 4
m
∼
N
(
(
N
+
μ
)
σ
2
,
2
(
N
+
2
μ
)
σ
4
)
)
.
m\sim {\mathcal N}\left((N+\mu)\sigma^2,2(N+2\mu)\sigma^4)\right).
m ∼ N ( ( N + μ ) σ 2 , 2 ( N + 2 μ ) σ 4 ) ) .
当
N
N
N
m
r
=
{
N
σ
2
;
H
0
(
N
+
μ
)
σ
2
;
H
1
m_r=\left\{ \begin{aligned} N\sigma^2;&\quad H_0\\ (N+\mu)\sigma^2;&\quad H_1 \end{aligned}\right.
m r = { N σ 2 ; ( N + μ ) σ 2 ; H 0 H 1
σ
r
2
=
{
2
N
σ
4
;
H
0
2
(
N
+
2
μ
)
σ
4
;
H
1
\sigma^2_r=\left\{ \begin{aligned} 2N\sigma^4;&\quad H_0\\ 2(N+2\mu)\sigma^4;&\quad H_1 \end{aligned}\right.
σ r 2 = { 2 N σ 4 ; 2 ( N + 2 μ ) σ 4 ; H 0 H 1
r
∼
N
(
m
r
,
σ
r
2
)
r\sim {\mathcal N}(m_r,\sigma^2_r)
r ∼ N ( m r , σ r 2 )
η
\eta
η
P
d
=
P
r
(
r
>
η
∣
H
1
)
=
Q
[
η
−
E
(
r
∣
H
1
)
V
a
r
(
r
∣
H
1
)
]
,
P_d={\rm Pr}(r>\eta|H_1)=Q\left[\frac{\eta-{\rm E}(r|H_1)}{\sqrt{{\rm Var}(r|H_1)}} \right],
P d = P r ( r > η ∣ H 1 ) = Q [ V a r ( r ∣ H 1 )
η − E ( r ∣ H 1 ) ] ,
P
f
=
P
r
(
r
>
η
∣
H
0
)
=
Q
[
η
−
E
(
r
∣
H
0
)
V
a
r
(
r
∣
H
0
)
]
.
P_f={\rm Pr}(r>\eta|H_0)=Q\left[\frac{\eta-{\rm E}(r|H_0)}{\sqrt{{\rm Var}(r|H_0)}} \right].
P f = P r ( r > η ∣ H 0 ) = Q [ V a r ( r ∣ H 0 )
η − E ( r ∣ H 0 ) ] .
P
d
P_d
P d
P
f
P_f
P f
P
m
=
1
−
P
d
.
P_m=1-P_d.
P m = 1 − P d .
P
m
P_m
P m
P
f
P_f
P f
α
=
1
\alpha=1
α = 1
P
m
P_m
P m
P
f
P_f
P f
γ
\gamma
γ
P
m
P_m
P m
P
f
P_f
P f
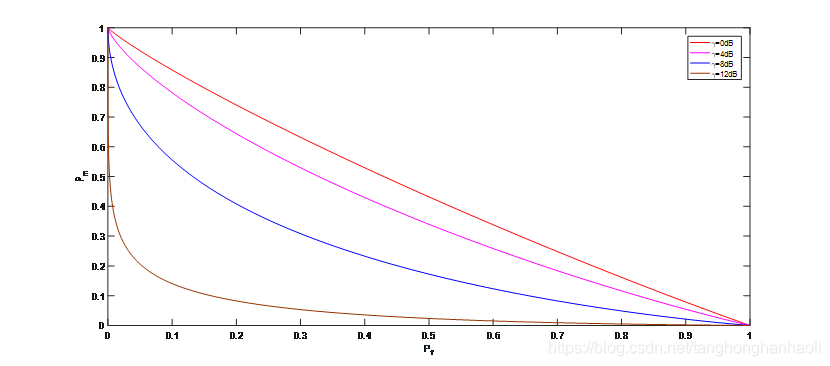 图1 漏检概率(
)与虚检概率(
)关系曲线
图1 漏检概率(
)与虚检概率(
)关系曲线