\(Description\)
你培育出了一些新型的神经元,它们可以有很多的轴突。
具体来说,对于第\(i\)个神经元,它有\(1\sim d_{i}\)条轴突,因此可以与\(1\sim d_{i}\)个神经元相连,可以将轴突看成无向图的边,假定每个神经元都是不同的。
现在你想知道,有多少种方案使得其中恰好\(k\)个神经元相连通,这里的连通需要保证任意两个神经元间有且仅有一条路径,方案数可能很大,你只需要对\(10^9+7\)取模输出。
两个方案是不同的当且仅当选择的神经元集合不同或其中有至少一条轴突\((u,v)\)出现在一个方案但不出现在另一个方案。
\(Input\)
第\(1\)行包含一个整数\(n\),表示神经元的个数。
第\(2\)行包含\(n\)个整数\(d_{i}\),表示第\(i\)个神经元最多的轴突数量\((1<=d_{i}<n)\)。
\(Output\)
输出\(1\)行,包含\(n\)个整数,第\(i\)个整数表示其中恰好有\(i\)个神经元连通的方案数模\(10^9+7\)后的值。
\(Sample Input\)
3
2 2 1
\(Sample Output\)
3 3 2
\(Hint\)
\(对于10\%的数据,n<=8\)
\(对于另外10\%的数据,di=n-1\)
\(对于20\%的数据,n<=15\)
\(对于30\%的数据,n<=20\)
\(对于40\%的数据,n<=50\)
\(对于60\%的数据,n<=70\)
\(对于100\%的数据,n<=100\)
1.思路
这道题,我们一看到题目,是要求方案数,还会很大,于是果断选择\(dp\)
我们发现题目有一个非常苛刻的要求:
两个方案是不同的当且仅当选择的神经元集合不同或其中有至少一条轴突(u,v)出现在一个方案但不出现在另一个方案。这个要求十分苛刻,于是我们考虑使用\(prufer\)序列。
中途强势植入
2.0 \(prufer\)序列的定义
\(prufer\)序列是无根树对应的一种序列,重点是一棵无根树对应一个唯一的prufer序列(不要问我怎么证)
把无根树转换为\(prufer\)序列的步骤:
- 将编号最小的叶子节点删除
- 将与这个节点相连的节点加入序列中
- 重复执行\(1,2\),直到这棵树只剩下两个节点
2.1 \(prufer\)序列的实现
我们来求一下\(prefer\)序列
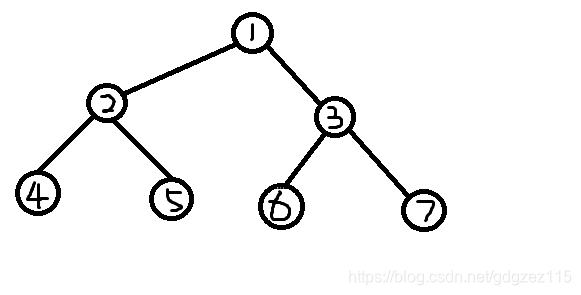
我们看一下上面这幅图
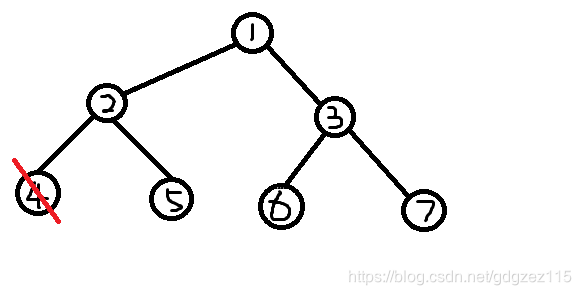
首先,我们删除编号最小的叶子节点\(4\),并将节点\(2\)加入序列中
\(prufer\)序列:\(2\)
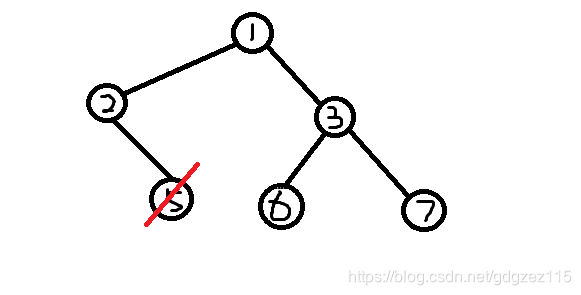
我们删除编号最小的叶子节点\(5\),将节点\(2\)加入序列
\(prufer\)序列:\(2,2\)
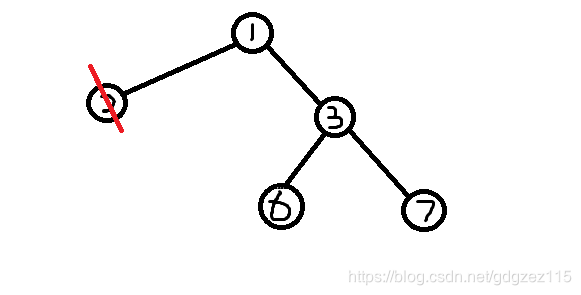
我们删除编号最小的叶子节点\(2\),将节点\(1\)加入序列
\(prufer\)序列:\(2,2,1\)
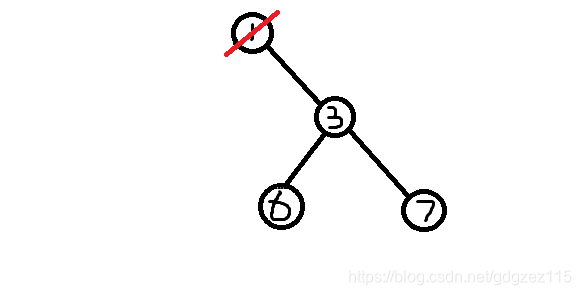
我们删除编号最小的叶子节点\(1\)(没有根),将节点\(3\)加入序列
\(prufer\)序列:\(2,2,1,3\)
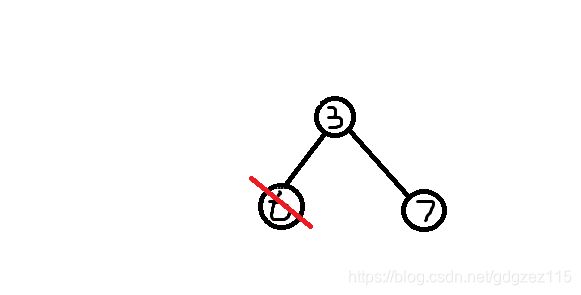
我们删除编号最小的叶子节点\(6\),将节点\(3\)加入序列
\(prufer\)序列:\(2,2,1,3,3\)
最后只剩下节点\(3,7\),这样就完成了\(prufer\)序列的实现
2.2 \(prufer\)序列的性质
- \(prufer\)序列中某个编号出现的个数为它的度数\(-1\)
- 一棵节点个数为\(n\)无根树的\(prufer\)序列长度一定是\(n-2\)
3.回归题目
大家现在应该知道\(prufer\)序列有什么用了吧
我们可以用\(prufer\)序列来完成题目的那个苛刻的要求
我们考虑有\(dp[i][j][k]\),表示枚举到了第\(i\)位,在序列中用了\(j\)个数,这些数在\(prufer\)序列中的个数有\(k\)个
我们分\(2\)种情况:取与不取
不取:\(dp[i+1[j][k]=dp[i+1][j][k]+dp[i][j][k]\)
取:如果取的话,我们枚举这个数用几次,设用\(l\)次,又因为你选了\(k+l\)个数,所以我们可以考虑这\(k\)个数放在\(k+l\)中,有\(C_{k+l}^k\)种情况
于是我们的状转方程为:
\(dp[i+1][j+1][k+l]=dp[i+1][j+1][k+l]+dp[i][j][k]*C_{k+l}^k\)
对于\(C_{k+l}^k\),我们可以\(O(\frac{(n+1)n}{2})\)预处理
代码:
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7,N=110;
typedef long long ll;
int d[N];
ll dp[N][N][N];
ll c[N][N];
int n;
void work()//C预处理
{
for(int i=0;i<=n;i++)
{
c[i][0]=1;
for(int j=1;j<=i;j++)
c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}
}
void solve()//dp方程
{
for(int i=0;i<n;i++)
{
for(int j=0;j<=i;j++)
{
for(int k=0;k<=n-2;k++)
{
if(dp[i][j][k])
{
dp[i+1][j][k]=(dp[i][j][k]+dp[i+1][j][k])%mod;
for(int l=0;l<=d[i+1]-1&&l+k<=n-2;l++)
dp[i+1][j+1][k+l]=(dp[i+1][j+1][k+l]+dp[i][j][k]*c[k+l][k])%mod;
}
}
}
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&d[i]);
dp[0][0][0]=1;
work();
solve();
printf("%d ",n);
for(int i=2;i<=n;i++)printf("%lld ",dp[n][i][i-2]);
return 0;
}