SP19148【INS14G - Kill them All】
感觉其他博客讲的不是很清楚,也没有说组合数公式是怎么来的,我这样数论极菜的萌新看了好久才想明白qwq。。
还是先给出本题组合数公式C(n-1,n/2)
分析
建议可以先看看关于卡特兰数的博客中对卡特兰数的应用,和这题很像,便于理解
把题目放到笛卡尔坐标系(平面直角坐标系)中考虑(如图1),x轴表示每个怪兽,从原点出发向右上方走表示由D杀了,向右下方走表示由S杀了。相当于我从原点出发,我的轨迹不能在过程中碰到x轴。
图1
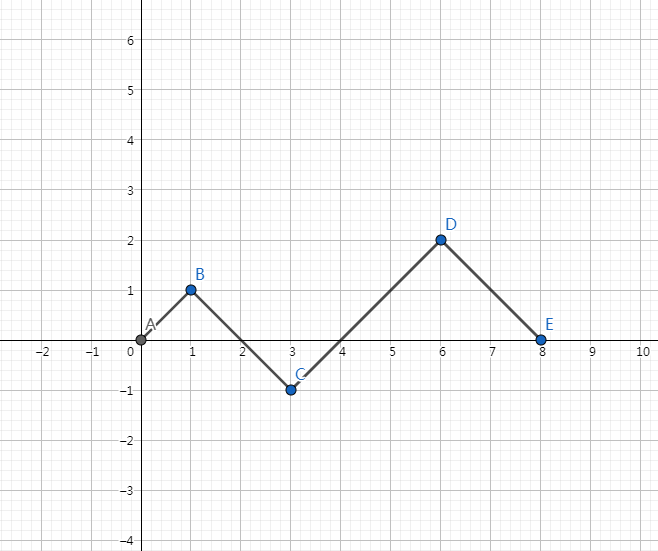
可知第一步一定向上,所以原题转化为从原点出发,轨迹在过程中不能跑到x轴下面。
枚举向上步数m,总方案数为C(n-1,m),现在我们要减去非法方案数。对于非法的轨迹,我们把它第一次碰到y=-1后的轨迹按y=-1翻转(如图2),在n,m确定的情况下,终点是确定的,翻转后的轨迹和原轨迹的方案一一对应。
那么终点在哪里呢? 设p为翻转后终点纵坐标,m为翻转前的向上步数,则有m - (n - m) + p = -2 (n-m为向下走的步数,翻转前终点纵坐标+1=翻转后纵坐标的相反数-1)-> p = -2 + n - 2m ,设当向上走x步时可以到达p,则 x - (n - x) = -2 + n - 2m -> x = n - m - 1,由于翻转后的轨迹和原轨迹的方案一一对应,所以到达p的方案数就是不合法的方案数
所以非法方案数为C(n,n-m-1)=C(n,m+1),(见组合数中的互补性质,即从m个不同元素中取出n个元素的组合数=从m个不同元素中取出(m-n)个元素的组合数)
向上步数为m的方案数为C(n,m)-C(n,m+1);
累加消掉中间项,答案为C(n,(n+1)/2)
由于n要减1,得C(n-1,n/2)。
组合数计算公式:c(m,n)=p(m,n)/n!=m!/((m-n)!×n!)
图2
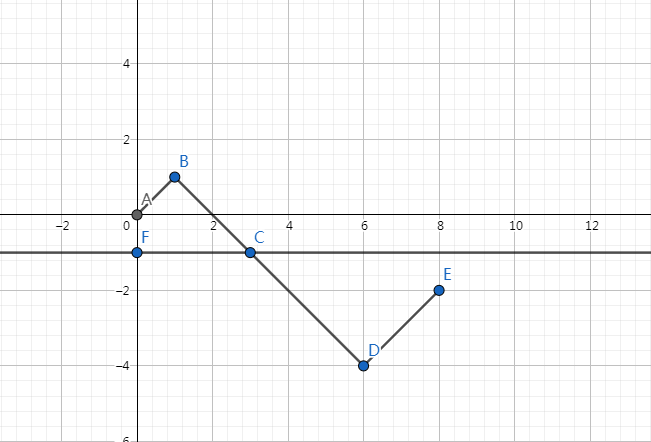
(以上思路由这个博客改进而来)
代码1
fac[i]存1~i的阶乘
inv[i]存1~i逆元的乘积
#include<cstdio>
using namespace std;
#define p 1000000007
long long fac[1000005],inv[1000005];
inline long long C(int n,int m) {
if (n==m || m==0) return 1;
return fac[n]*inv[m]%p*inv[n-m]%p;
}
int main() {
int T,n;
scanf("%d",&T),fac[0]=inv[0]=inv[1]=1;
for (int i=1; i<1000005; i++) fac[i]=fac[i-1]*i%p;
for (int i=2; i<1000005; i++) inv[i]=p-(p/i)*inv[p%i]%p;
for (int i=2; i<1000005; i++) inv[i]=inv[i-1]*inv[i]%p;
while(T--)
scanf("%d",&n),printf("%lld\n",C(n-1,n/2));
}代码2
#include<cstdio>
using namespace std;
#define p 1000000007
#define int long long
int fac[1000005];
inline int pow(int x) {
int ans=1;
x%=p;
for (int i=p-2; i; i>>=1,x=x*x%p)
if (i&1) ans=ans*x%p;
return ans;
}//快速幂求逆元(x^(p-2))
signed main() {
int T,n;
scanf("%lld",&T),fac[0]=1;
for (int i=1; i<=1000005; i++) fac[i]=fac[i-1]*i%p;
while(T--)
scanf("%lld",&n),printf("%lld\n", fac[n-1]*pow(fac[n/2]*fac[n-1-n/2]%p)%p);
}通过这题的确对组合数的应用加深了不少,如果分析有误还望指出qwq!