理论基础
轮换与对换
概念:把 $S$ 中的元素 $i_1$ 变成 $i_2$,$i_2$ 变成 $i_3$ ... $i_k$ 又变成 $i_1$,并使 $S$ 中的其余元素保持不变的置换称为循环,又称轮换,记为 $(i_1, i_2,...,i_k)$,$k$ 称为循环长度,特别地,循环长度为2的循环称为对换。
定理:
(1)任一置换可表示成若干个无公共元素的循环之积
(2)任一置换可表示成若干个对换之积,且对换个数的奇偶性不变。
八数码中的置换
若一个置换可以分解成奇数个对换之积称为奇置换,否则称为偶置换.
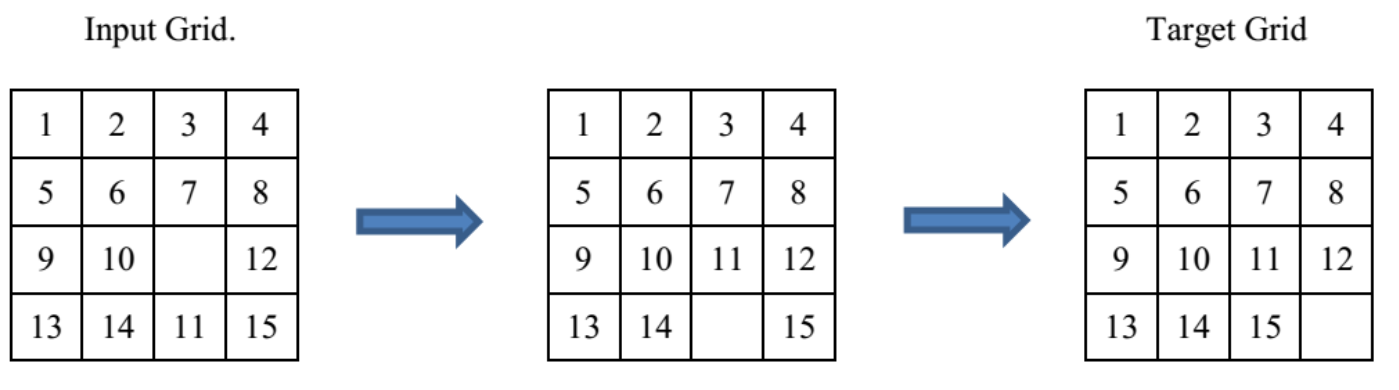
即进行如下置换:
$$\begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 0 & 12 & 13 & 14 & 11 & 15\\
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 0
\end{pmatrix}$$
等价于轮换之积:
$\begin{pmatrix}
0 & 11 & 15\\
11 & 15 & 0
\end{pmatrix} = \left ( 0 \ 11 \ 15\right ) = (0 \ 11)(0 \ 15)$