《终结篇》全体自然数的和等于-1/12???我觉得我还可以再抢救一下

版权声明：Victor Miller https://blog.csdn.net/qq_40155097/article/details/86670230

全体自然数的和等于-1/12，你八成听说过这个说法，对不对？！

实际上，我的不少朋友不但是听说过这个说法，而且是真的相信了，真的是按照字面上理解这个说法。这样一来，就造成了严重的矛盾：自然数依次相加，不是应该越来越大，超过任何限制吗？怎么可能得到一个固定的值？更不可思议的是，怎么还能得到一个负值？正数加正数只可能得到正数，怎么会变成负数？

按照这样想下去，就越想越可怕了。难道常识都是靠不住的？难道数学是一门违反常识的学科？难道数学家是一群阴谋家，他们向大众隐瞒了许多可怕的秘密？……

于是乎，我的不少朋友就来忧心忡忡地问我。用他们的话说，简直是世界观都要崩溃了！
好吧，我们就借这个机会，向大家讲清楚这个所谓“全体自然数的和等于-1/12”以及 $\sum\limits_{n=0}^\infty (-1)^n=\frac{1}{2}$是怎么回事。正如那句俗话所说：我觉得我还可以再抢救一下

首先要从欧拉讲起

欧拉曾经研究过一个级数求和的问题，我们管它叫
$\LARGE \varepsilon(s)$
$\Large \varepsilon(s)=\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\cdots$

1.当s=1时

$\large\varepsilon(1)=1+\frac{1}{2}+\frac{1}{3}+\cdots$
看这个数越往后越小，所以它应该时会收敛的对吧。

错！

我们来变个形：
$\begin{aligned} \large\varepsilon(1)&=1+\frac{1}{2}+\frac{1}{3}+\cdots\\[2ex] &=1+\frac{1}{2}+\left(\frac{1}{3}+\frac{1}{4}\right)+\left(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\right)+\cdots \\[2ex] &=1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\cdots \end{aligned}$
所以当s=1时 $\varepsilon(1)$是无穷大的。

2.当s>1时

$\large\varepsilon(s)$时无限趋近于某个值的，所以它是收敛的。
举个栗子：
当s=2时
$\begin{aligned} \large\varepsilon(2)&=1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots \\[2ex] &=\frac{π^2}{6} \end{aligned}$
其实这也是一个计算π比较简便的方法。

3.当s<1时

这时，我们的欧拉就要登场了。
欧拉算了几个 $\varepsilon(s)$的值
$\varepsilon(-1)=1+2+3+\cdots=-\frac{1}{12}$
$\varepsilon(-2)=0$
$\varepsilon(-3)=\frac{1}{120}$
看到这里你也许会问这怎么可能，它们应该是发散的啊，怎么可能是一个具体的值。
的确欧拉算错了。我们来看一下欧拉算 $\varepsilon(-1)$的方法。
他展开（幂级数展开）了一个函数： $\Large\frac{x}{(1-x)^2}$并令x=-1
$\begin{aligned} \frac{x}{(1-x)^2}&amp;=x+2x^2+3x^3+\cdots \\[2ex] -\frac{1}{4}&amp;=-1+2-3+4-5+6-\cdots \\[2ex] &amp;=-(1+3+5+\cdots)+(2+4+6+\cdots) \\[2ex] &amp;=-(1+2+3+4+5+6+\cdots)+(2*2+4*2+6*2+\cdots) \\[2ex] &amp;=3(1+2+3+4+5+\cdots) \\[2ex] \therefore1+2+3+\cdots &amp;=-\frac{1}{12} \end{aligned}$

没错，这是一个小学生都能看的懂的证明，不过我相信一个中学文化水平的人就已经能察觉到充斥在证明过程中的别扭感了。当然，如果你是一个大学生，并且在微积分的课堂上还算听过课，那么一定能一针见血的指出视频中这些证明的一个巨大的bug：

在无穷级数中，只有绝对收敛的无穷级数才可以重新排列各项而不改变收敛值。也就是说，对于非绝对收敛的无穷级数，不能任意更改求和次序！这也就是黎曼(Riemann)级数定理，也叫黎曼重排定理。

可以说，证明过程充斥着民科的味道，无时不刻不在肆意改变着级数求和的次序，用一些看起来精巧的“移项变号”、“错位相减”的手法，得到了一个似乎正确的让人信服的结果。可惜的是，从严谨的数学角度上看，上面所有的证明过程，完全不成立。
那么怎么解决这个问题呢？
接下来有请我们的解析延拓登场

解析延拓

解析延拓的定义在这里就不在多说了。
但解析延拓有个规则：处处可导。什么意思呢，其实就是处处无限光滑。
为了让大家更了解解析延拓
我们来举个栗子：

在中学时，我们都学过这样的数列：

$1+x+x^2+x^3+\cdots$
利用等比数列求和公式，我们可以求出它的值，但前提是 $|x|&lt;1$
$1+x+x^2+x^3+\cdots=\frac{1}{1-x} \tag{|x|&lt;1}$
为什么呢，因为当 $|x|\geq1$时左边是发散的而不是收敛的，所以这时左边和右边是不相等的，它就是无意义的了。
我们现在把它的函数图像画出来。

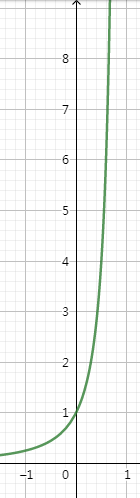
左边的函数只有在(-1,1)这个范围内才有意义。
那么问题来了，右边的函数也是在这个范围才有意义吗？
不是吧。只要 $x\neq1$它就有意义。
那么如果我们把右边的函数图像画出来就相当于把左边的函数给延拓了。

那么现在它的定义域就变大了，原本只在(-1,1)的范围内有意义，但现在除了1这个点外其他的点都有意义。
所以我们现在可以说当 $|x|&lt;1$时左右两边完全相等，当 $x\neq1$时，左边的式子没有意义但右边的式子仍然有意义。
这时我们带入一些特殊值，就会得到一些奇怪的结果。

1.当 $x=\frac{1}{2}时$

$1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots=2$
这个是成立的左右两边严格相等。

2.当 $x=-1$时

$左边=1-1+1-1+\cdots \tag{这个式子已经没有含义了}$
$右边=\frac{1}{2} \tag{这是解析延拓之后的函数，是有意义的}$
现在我们就来到了第一个问题 $\sum\limits^{\infty}_{n=1}(-1)^n=\frac{1}{2}?$
那它们相不相等呢？
—————————————————————————————————————————这部分可以忽略
$\large\sum\limits_{n=0}^\infty (-1)^n=\frac{1}{2}$这个问题依赖于数列极限的定义。
考虑 Cauchy 的数列极限定义：
如果部分和数列 $\large S_n(S_n=\sum_{i=1}^n a_i)$收敛于有限数 $s$，则对于任意 $\varepsilon&gt;0$，存在正整数 $N$当 $n&gt;N$时， $\large|S_n-s|&lt;\varepsilon$。即加的项数足够多以后，部分和 $\large S_n$与 $s$“要多接近有多接近”。
在上面的定义下级数 $\large\sum\limits_{n=0}^\infty (-1)^n$是不收敛的。这可以通过Cauchy收敛定理加以说明：任何收敛的级数其通项必须趋于0。显然这个交错级数不满足这一性质。其实从上面的定义中可以看出部分和在0和1之间来回震荡，不可能稳定于某个 $s$
数学家为了让这样的数列收敛，就修改了数列收敛的定义。其中一个就是 Cesaro 平均收敛。所谓平均收敛, 只要求 $\Large\lim\limits_{n\to\infty}\frac{\sum\limits_{i=1}^n S_i}{n}$收敛即可，即相当于对 $S_n$求平均值。在这个意义下级数收敛： $S_n$在0和1之间来回震荡，它的平均值是 $\large\frac{1}{2}$。
所以 $\sum\limits_{n=0}^\infty (-1)^n$收敛与否，归根结底是我们对“和”的定义不同。但要指出，Cesaro 和与 Cauchy 和的定义是相容的：如果一个数列在 Cauchy 和的意义下收敛于 $s$，则在 Cesaro 和的意义下也收敛于 $s$，但反之不然。
—————————————————————————————————————————忽略部分结束
简单点：如果你说它相等，那你的意思就是说一个无意义的数就因为解析延拓就变成了一个有意义的数，这是不是很不合理啊。所以说这种方法是不对的，当时欧拉就犯了一个这样的错误。
$\large但欧拉就是欧拉，他方法错了但是结果对了。$
那么这个答案是谁确定的呢？

黎曼函数

这个答案就是黎曼确定的。

这样我们就讲到了黎曼函数。
黎曼把欧拉研究的这个级数进行了解析延拓，称之为黎曼函数：
$\LARGE\zeta(s)$
我们可以这样理解它
$\large当s&gt;1且s\in R$时
它完全和欧拉研究的级数一样
$\large当s\neq1且s\in C$时
$\large\zeta(s)=\frac{1}{\varGamma(s)}\int_{0}^{\infty}\frac{x^{s-1}}{e^x-1}$
可能有人会问这是什么东西啊？
你不用管它是什么东西，它只是把刚刚的欧拉级数通过处处可导的解析延拓方式得到的一个新的函数而已。
这个函数除了复平面内1这个点外它都是有意义的，而且如果我们代一些特殊的值进去就会得到很多奇怪的结果
比如说：
$\zeta(-1)=-\frac{1}{12}$
$\zeta(-2)=0$
$\zeta(-3)=\frac{1}{120}$
因此有人就说了：你看 $\zeta(-1)$的含义就是全体自然数的和，所以全体自然数的和是 $\large-\frac{1}{12}$
这个说法对不对？ $\\[2ex]$
$\Huge不对！\\[2ex]$
$\Large为什么？$
因为 $s=-1$根本不在欧拉级数的定义域内，所以你把 $-1$代到欧拉级数内是没有意义的,而这个 $-1$是在 $\zeta$的范围之内的。而且其级数定义可没说随着延拓出去啊！ $-\frac{1}{12}$归根结底只是黎曼 $\zeta$函数的函数值，并不是自然数级数的值,而这个“和”也不是普通意义上的和。所以这个值是不能与原来的欧拉级数的意义相对应的。
$\Huge\therefore\textcolor{red}{\sum\limits^{\infty}_{n=1}n\neq -\frac{1}{12}}$
$\large等一下！$
然而，真的到此为止了吗？全体自然数之和等于 $-\frac{1}{12}$，物理上确实已经有相应的实验从统计量角度验证了这个等式的成立如果是错的，为什么此结果在复分析、量子力学及弦理论等领域中有着深刻的影响与应用？
我们应该更冷静的思考一下，这式子的背后究竟是什么……

$\large\textcolor{red}{其实我认为这个问题的来源于对数学中定义的滥用，以及人们对定义的误解。}$

数学家是这个世界上最严谨的一批人，他们谈论什么都有据可循。事实上，数列极限本身就是一个有严格定义的概念。所有学过微积分的同学不妨问自己
$\large\sum\limits^{\infty}_{n^2}=\frac{π^2}{6}$中这个等号的意义是什么,和 $1+1=2$中的等号是否意义相同？
就像一个严肃的数学家绝对不会轻易写下 $\large\sum\limits^{\infty}_{n=1}\frac{1}{n^2}=\frac{1}{2}$,而是可能会告诉你这是在 Cesaro 和意义下的结果或是解析延拓意义下的结果，这里等号的意义已不是 $\large\sum\limits^{\infty}_{n^2}=\frac{π^2}{6}$或 $1+1=2$中的等号的意义。
至于在解析延拓的意义下 $\sum\limits_{n=1}^\infty n=-\frac{1}{12}$这个式子为何会有物理上的效应，这是另外一个问题。粗略地说是因为解析延拓可以反映求和的某些渐进行为。而这背后蕴含的则是物理中正规化的方法和重整化的思想。

(全篇终)