一、基本概念
所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。
贪心算法没有固定的算法框架,算法设计的关键是贪心策略的选择。必须注意的是,贪心算法不是对所有问题都能得到整体最优解,选择的贪心策略必须具备无后效性,即某个状态以后的过程不会影响以前的状态,只与当前状态有关。
所以对所采用的贪心策略一定要仔细分析其是否满足无后效性。
二、基本思路
1.建立数学模型来描述问题。
2.把求解的问题分成若干个子问题。
3.对每一子问题求解,得到子问题的局部最优解。
4.把子问题的解局部最优解合成原来解问题的一个解。
三、算法实现
- 从问题的某个初始解出发。
- 采用循环语句,当可以向求解目标前进一步时,就根据局部最优策略,得到一个部分解,缩小问题的范围或规模。
- 将所有部分解综合起来,得到问题的最终解。
从问题的某一初始解出发; while (能朝给定总目标前进一步) { 利用可行的决策,求出可行解的一个解元素; } 由所有解元素组合成问题的一个可行解;
四、(一)贪心算法之活动安排
- 问题描述:
设有n个活动的集合E={1,2,…,n},其中每个活动都要求使用同一资源,如演讲会场等,而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间si和一个结束时间fi,且si <fi 。要求设计程序,使得安排的活动最多。

问题分析:
活动安排问题要求安排一系列争用某一公共资源的活动。用贪心算法可提供一个简单、漂亮的方法,使尽可能多的活动能兼容的使用公共资源。设有n个活动的集合{0,1,2,…,n-1},其中每个活动都要求使用同一资源,如会场等,而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间starti和一个结束时间endi,且starti<endi。如选择了活动i,则它在半开时间区间[starti,endi)内占用资源。若区间[starti,endi)与区间[startj,endj)不相交,称活动i与活动j是相容的。也就是说,当startj≥endi或starti≥endj时,活动i与活动j相容。活动安排问题就是在所给的活动集合中选出最多的不相容活动。
活动安排问题就是要在所给的活动集合中选出最大的相容活动子集合,是可以用贪心算法有效求解的很好例子。该问题要求高效地安排一系列争用某一公共资源的活动。贪心算法提供了一个简单、漂亮的方法使得尽可能多的活动能兼容地使用公共资源。
算法设计:
若被检查的活动i的开始时间starti小于最近选择的活动j的结束时间endj,则不选择活动i,否则选择活动i加入集合中。运用该算法解决活动安排问题的效率极高。当输入的活动已按结束时间的非减序排列,算法只需O(n)的时间安排n个活动,使最多的活动能相容地使用公共资源。如果所给出的活动未按非减序排列,可以用O(nlogn)的时间重排。
代码实现:
#include<iostream> #include<algorithm> using namespace std; struct actime{ int start,finish; }act[1002]; bool cmp(actime a,actime b){ return a.finish<b.finish; } int main(){ int i,n,t,total; while(cin>>n){//活动的个数 for(i=0;i<n;i++){ cin>>act[i].start>>act[i].finish; } sort(act,act+n,cmp);//按活动结束时间从小到大排序 t=-1; total=0; for(i=0;i<n;i++){ if(t<=act[i].start){ total++; t=act[i].finish; } } cout<<total<<endl; } return 0; }
四、(二)贪心算法之哈夫曼算法
核心思想:贪心算法:利用局部最优推出全局最优。
其核心思想:每次取数值最小的两个结点,将之组成一颗子树,并移除原来的两个点。
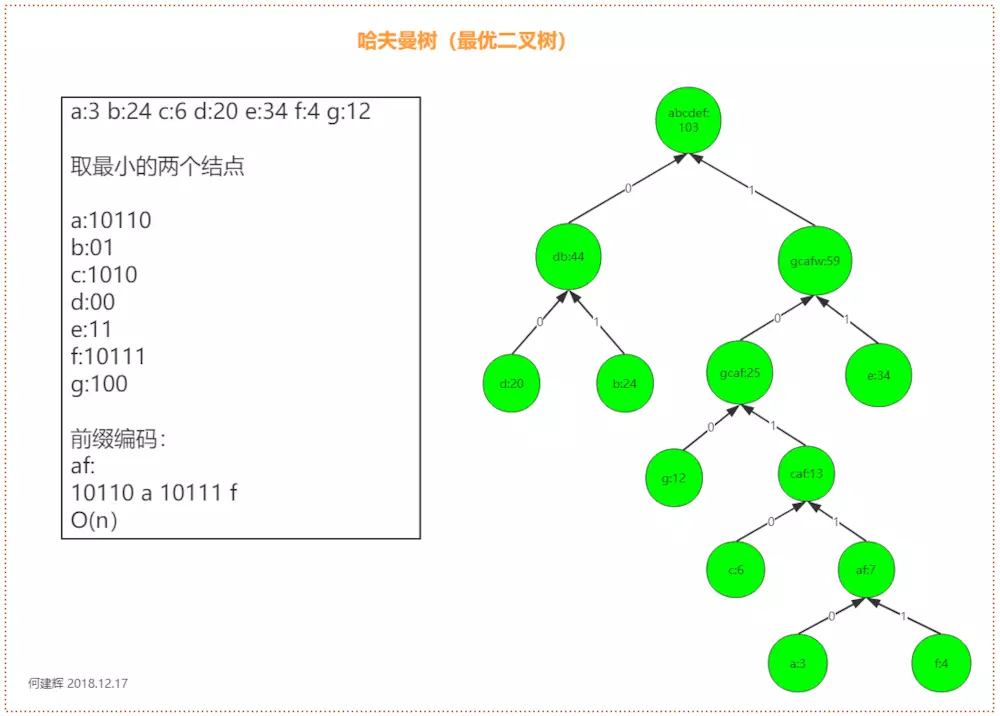
哈夫曼的构造:
哈夫曼树在构造时每次从备选节点中挑出两个权值最小的节点进行构造,每次构造完成后会生成新的节点,将构造的节点从备选节点中删除并将新产生的节点加入到备选节点中。新产生的节点权值为参与构造的两个节点权值之和。举例如下:
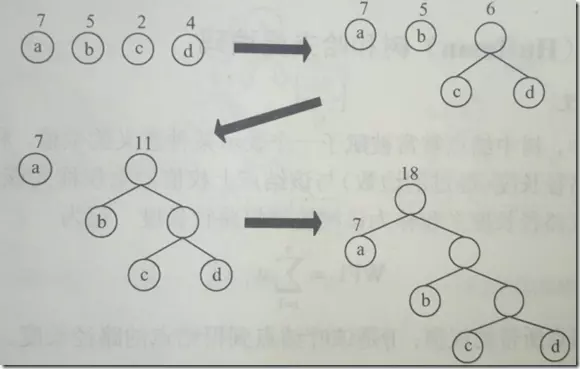
备选节点为a,b,c,d,权值分别为7,5,2,4
选出c和d进行构造(权值最小),生成新节点为e(权值为6),备选节点变为7,5,6
选出b和e进行构造,生成新节点f(权值为11),备选节点为7,11
将最后的7和11节点进行构造,最后生成如图所示的哈夫曼树
哈夫曼的应用
在处理字符串序列时,如果对每个字符串采用相同的二进制位来表示,则称这种编码方式为定长编码。若允许对不同的字符采用不等长的二进制位进行表示,那么这种方式称为可变长编码。可变长编码其特点是对使用频率高的字符采用短编码,而对使用频率低的字符则采用长编码的方式。这样我们就可以减少数据的存储空间,从而起到压缩数据的效果。而通过哈夫曼树形成的哈夫曼编码是一种的有效的数据压缩编码。
如果没有一个编码是另一个编码的前缀,则称这样的编码为前缀编码。如0,101和100是前缀编码。由前缀码形成的序列可以被唯一的组成一个字符串序列。如00101100可以被唯一的分析为0,0,101和100。
示例:
我们对一个字符串进行统计发现a-f出现的频率分别为a:45,b:13,c:12,d:16,e:9,f:5,我们对该字符串进行采用哈夫曼编码进行存储。

四、(三)贪心算法之单元最短路径 传送门
最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径。
算法具体的形式包括:
- 确定起点的最短路径问题:即已知起始结点,求最短路径的问题。适合使用Dijkstra算法。
- 确定终点的最短路径问题:与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题。在无向图中该问题与确定起点的问题完全等同,在有向图中该问题等同于把所有路径方向反转的确定起点的问题。
- 确定起点终点的最短路径问题:即已知起点和终点,求两结点之间的最短路径。
- 全局最短路径问题:求图中所有的最短路径。适合使用Floyd-Warshall算法。
主要介绍以下几种算法:
- Dijkstra最短路算法(单源最短路)
- Bellman–Ford算法(解决负权边问题)
- SPFA算法(Bellman-Ford算法改进版本)
- Floyd最短路算法(全局/多源最短路)
以Dijkstra最短路算法(单源最短路)举例
算法介绍:
迪科斯彻算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题,算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。
指定一个起始点(源点)到其余各个顶点的最短路径,也叫做“单源最短路径”。例如求下图中的1号顶点到2、3、4、5、6号顶点的最短路径。
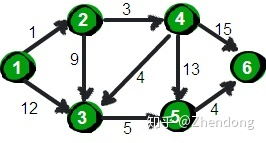
使用二维数组e来存储顶点之间边的关系,初始值如下。
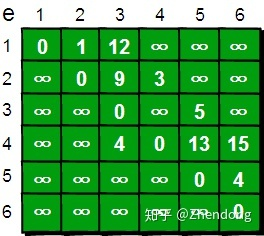
我们还需要用一个一维数组dis来存储1号顶点到其余各个顶点的初始路程,如下。

将此时dis数组中的值称为最短路的“估计值”。
既然是求1号顶点到其余各个顶点的最短路程,那就先找一个离1号顶点最近的顶点。通过数组dis可知当前离1号顶点最近是2号顶点。当选择了2号顶点后,dis[2]的值就已经从“估计值”变为了“确定值”,即1号顶点到2号顶点的最短路程就是当前dis[2]值。
既然选了2号顶点,接下来再来看2号顶点有哪些出边呢。有2->3和2->4这两条边。先讨论通过2->3这条边能否让1号顶点到3号顶点的路程变短。也就是说现在来比较dis[3]和dis[2]+e[2][3]的大小。其中dis[3]表示1号顶点到3号顶点的路程。dis[2]+e[2][3]中dis[2]表示1号顶点到2号顶点的路程,e[2][3]表示2->3这条边。所以dis[2]+e[2][3]就表示从1号顶点先到2号顶点,再通过2->3这条边,到达3号顶点的路程。
这个过程有个专业术语叫做“松弛”。松弛完毕之后dis数组为:

接下来,继续在剩下的3、4、5和6号顶点中,选出离1号顶点最近的顶点4,变为确定值,以此类推。
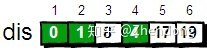
最终dis数组如下,这便是1号顶点到其余各个顶点的最短路径。
 核心代码:
核心代码:
//Dijkstra算法核心语句 for(i=1;i<=n-1;i++) { //找到离1号顶点最近的顶点 min=inf; for(j=1;j<=n;j++) { if(book[j]==0 && dis[j]<min) { min=dis[j]; u=j; } } book[u]=1; for(v=1;v<=n;v++) { if(e[u][v]<inf) { if(dis[v]>dis[u]+e[u][v]) dis[v]=dis[u]+e[u][v]; } } }
四、(四)贪心算法之最小生成树 传送门 传送门【推荐】
在含有n个顶点的连通图中选择n-1条边,构成一棵极小连通子图,并使该连通子图中n-1条边上权值之和达到最小,则称其为连通网的最小生成树。
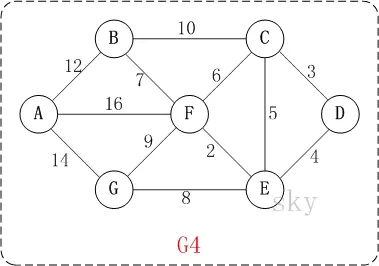
例如,对于上图中的连通网可以有多棵权值总和不相同的生成树。
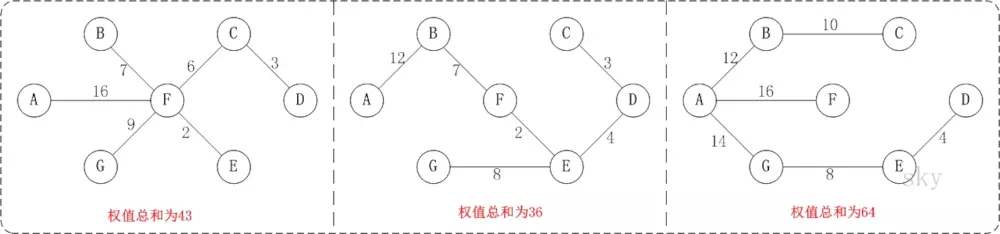
Kruskal算法
基本思想:按照权值从小到大的顺序选择n-1条边,并保证这n-1条边不构成回路。
具体做法:首先构造一个只含n个顶点的森林,然后依照权值从小到大从连通网中选择边加入到森林中,并使得森林不产生回路,直到森林变成一棵树为止。
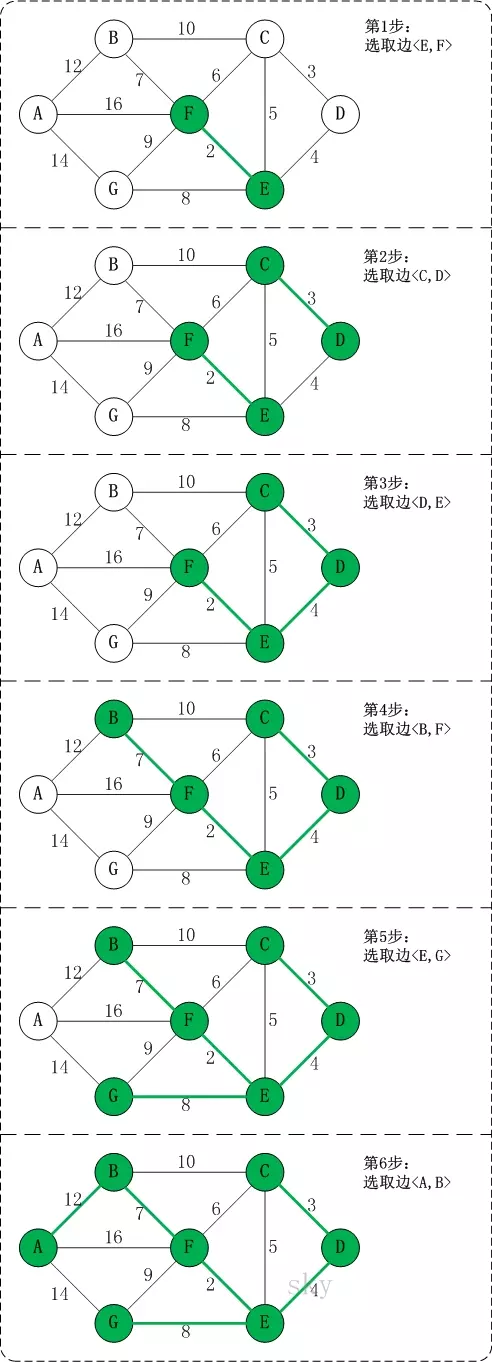
第1步:将边<E,F>加入R中。
边<E,F>的权值最小,因此将它加入到最小生成树结果R中。
第2步:将边<C,D>加入R中。
上一步操作之后,边<C,D>的权值最小,因此将它加入到最小生成树结果R中。
第3步:将边<D,E>加入R中。
上一步操作之后,边<D,E>的权值最小,因此将它加入到最小生成树结果R中。
第4步:将边<B,F>加入R中。
上一步操作之后,边<C,E>的权值最小,但<C,E>会和已有的边构成回路;因此,跳过边<C,E>。同理,跳过边<C,F>。将边<B,F>加入到最小生成树结果R中。
第5步:将边<E,G>加入R中。
上一步操作之后,边<E,G>的权值最小,因此将它加入到最小生成树结果R中。
第6步:将边<A,B>加入R中。
上一步操作之后,边<F,G>的权值最小,但<F,G>会和已有的边构成回路;因此,跳过边<F,G>。同理,跳过边<B,C>。将边<A,B>加入到最小生成树结果R中。
此时,最小生成树构造完成!它包括的边依次是:<E,F> <C,D> <D,E> <B,F> <E,G> <A,B>。
3.算法分析
根据前面介绍的克鲁斯卡尔算法的基本思想和做法,我们能够了解到,克鲁斯卡尔算法重点需要解决的以下两个问题:
问题一 对图的所有边按照权值大小进行排序。
问题二 将边添加到最小生成树中时,怎么样判断是否形成了回路。
问题一用排序算法排序即可。
问题二处理方式:记录顶点在“最小生成树”中的终点,顶点的终点是“在最小生成树中与它连通的最大顶点"(关于这一点,后面会通过图片给出说明)。然后每次需要将一条边添加到最小生成树时,判断该边的两个顶点的终点是否重合,重合的话则会构成回路。 以下图来进行说明:
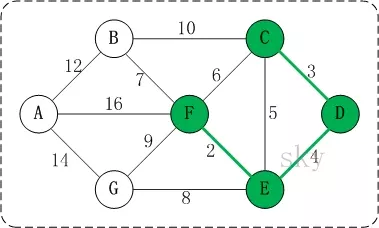
在将<E,F> <C,D> <D,E>加入到最小生成树R中之后,这几条边的顶点就都有了终点:
(01) C的终点是F。 (02) D的终点是F。 (03) E的终点是F。 (04) F的终点是F。
关于终点,就是将所有顶点按照从小到大的顺序排列好之后;某个顶点的终点就是"与它连通的最大顶点"。 因此,接下来,虽然<C,E>是权值最小的边。但是C和E的重点都是F,即它们的终点相同,因此,将<C,E>加入最小生成树的话,会形成回路。这就是判断回路的方式。