Neural Networks Learning(神经网络学习)

前言

这一章还是紧接上一章的内容，在上一章我们介绍了为什么需要用神经网络，神经网络的模型是怎样构造的，还有神经网络在生活中的应用，在这一章，我会详细地给大家介绍神经网络的学习，它是如何通过Forward propagation(正向传播)和Backpropagation(反向传播)结合来更好地进行学习的。

最后，如果有的地方理解不对，请大家不吝赐教，谢谢！

第七章 Neural Networks Learning(神经网络学习)

7.1 Cost function(代价函数)

在前面给大家介绍的线性回归和逻辑回归问题时，都会引入代价函数，在这里我们同样也需要给出代价函数，在前面也向大家说明了代价函数的作用，即判断一个学习算法是否有效，在这里我们给大家介绍的问题还是分类问题，模型如图1所示。

图1 神经网络(分类问题)模型

在这个模型中，当我们只有一个输出时，我们的结果就是两个：0和1，而当我们的输出不止一个时，即我们的类别不止一种，这个时候结果就是 $y\in R^{k}$ (一共有k种类别)，例如有4种类别时， $\begin{bmatrix} 1\\0 \\ 0 \\ 0 \end{bmatrix}$ 、 $\begin{bmatrix} 0\\1 \\ 0 \\ 0 \end{bmatrix}$ 、 $\begin{bmatrix} 0\\0 \\ 1 \\ 0 \end{bmatrix}$ 、 $\begin{bmatrix} 0\\0 \\ 0 \\ 1 \end{bmatrix}$ 分别代表不同的种类。还有我们用L来表示整个模型一共有多少层，例如图1，就一共有4层，则L=4，我们用 $S_{l}$ 来表示每一层有多少个单元，不包括偏置单元，例如图1中的第二层就一共有5个单元，则 $S_{l}$ =5。

给大家回忆了前面关于神经网络的基础构造以后，由于这是一个逻辑分类的问题，在前面我们也给大家讲解了逻辑回归问题中的代价函数是： $J(\theta )=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}logh(x^{(i)})+(1-y^{(i)})log(1-h(x^{(i)}))]+\frac{\lambda }{2m}\sum_{j=1}^{n}\theta _{j}^{2}$ ，而我们的神经网络中，我们的输出结果不止一种，所以这个时候的代价函数是： $J(\Theta )=-\frac{1}{m}[\sum_{i=1}^{m}\sum_{k=1}^{K}y_{k}^{(i)}log(h_{\Theta }(x^{(i)}))_{k}+(1-y_{k}^{(i)})log(1-(h_{\Theta }(x^{(i)}))_{k})]+\frac{\lambda }{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{s_{l}}\sum_{j=1}^{s_{l}+1}(\Theta _{ji}^{l})^2$

这个还是有正则化的。同样我们在这里需要做的就是使J( $\Theta$ )最小，而我们前面给大家介绍的做法是对J( $\Theta$ )关于 $\Theta$ 求导，并令其为0，然后求出的对应的 $\Theta$ 。

6.2 Backpropagation(反向传播)

在这里我将给大家介绍一个新的算法，来计算J( $\Theta$ )关于 $\Theta$ 的偏导，也是这节的重点Backpropagation(反向传播)算法，在前一章节我们有由输入层一步步地到输出层的算法称为正向传播，反向传播顾名思义就是我们是从输出到输入的过程。在这里我们用 $\delta _{j}^{(l)}$ 来表示第l层第j个单元的误差，还是拿图1的模型来做解释，对于第4层输出层的误差来说， $\delta _{j}^{(4)}=a_{j}^{(4)}-y_{j}$ ，即我们通过前向传播得到的输出和我们实际的输出之间的一个差值，也可以简化为 $\delta^{(4)}=a^{(4)}-y$ ， $\delta ^{(3)}=(\Theta ^{(3)})^{\top }\delta ^{(4)}.*g'(z^{(3)})$ (其中 $g'(z^{(3)})=a^{(3)}.*(1-a^{(3)})$ )，同理 $\delta ^{(2)}=(\Theta ^{(2)})^{\top }\delta ^{(3)}.*g'(z^{(2)})$ (其中 $g'(z^{(2)})=a^{(2)}.*(1-a^{(2)})$ )，没有 $\delta ^{(1)}$ ，因为我们默认从输入得到的数据没有误差，至于以上给大家介绍的误差公式是一些数学的推导，不需要深入钻研，说实话，我也没怎么特别理解。这个过程就是一步步地从输出算到输入，而我们前面所要求的 $\frac{\partial }{\partial \Theta _{ij}^{(l)}}J(\Theta )=a_{j}^{(l)}\delta _{i}^{(l+1)}$ (忽略 $\lambda$ ， $\lambda$ =0)。

下面来给大家总结一下Backpropagation算法：

我们的训练集有{ ${(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})}$ }

令 $\Delta _{ij}^{(l)}=0$ (用来计算 $\frac{\partial }{\partial \Theta _{ij}^{(l)}}J(\Theta )$ )

for i=1to m $\leftarrow$ ( $x^{(i)},y^{(i)}$ )

set $a^{(1)}=x^{(i)}$

perform forward propagation to compute $a^{(l)}$ (l=2,3,...,L)

using $y^{(i)}$ ,compute $\delta ^{(L)}=a^{(L)}-y^{(i)}$

compute $\delta ^{(L-1)},\delta ^{(L-2)},...,\delta ^{(2)}$

$\Delta _{ij}^{(l)}:=\Delta _{ij}^{(l)}+a_{j}^{(l)}\delta _{i}^{(l+1)}$ $\Rightarrow \Delta ^{(l)}:=\Delta ^{(l)}+\delta ^{(l+1)}(a^{(l)})^\top$

$D_{ij}^{(l)}:=\frac{1}{m}\Delta _{ij}^{(l)}+\lambda \Theta _{ij}^{(l)}$ if $j\neq 0$

$D_{ij}^{(l)}:=\frac{1}{m}\Delta _{ij}^{(l)}$ if $j= 0$ $\frac{\partial }{\partial \Theta _{ij}^{(l)}}J(\Theta )$ = $D_{ij}^{(l)}$

6.3 关于Forward Propagation和Backpropagation总结

通过前面对Backpropagation的讲解，大家可能还是对Backpropagation到底在做什么不是很了解，在这一节，我将通过图形的方式直观地带大家了解整个算法的过程也会和Forward Propagation做一个比较。

1）Forward Propagation(正向传播)

图2 Forward Propagation

在图2中，我们可以看到，这是一个4层的神经网络，例如第3层的 $z_{1}^{(3)}=\Theta _{10}^{(2)}+\Theta _{11}^{(2)}a_{1}^{(2)}+\Theta _{12}^{(2)}a_{2}^{(2)}$ ，而 $a_{1}^{(3)}=$ g( $z_{1}^{(3)}$ )通过这样从输入层传到输出层。

2）Backpropagation(反向传播)

那Backpropagation到底是在做一个什么工作了？

对于代价函数 $J(\theta )=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}logh_{\Theta }(x^{(i)})+(1-y^{(i)})log(1-h_{\Theta }(x^{(i)}))]+\frac{\lambda }{2m}\sum_{l=1}^{L}\sum_{i=1}^{s_{l}}\sum_{j=1}^{s_{l}+1}(\Theta _{ij}^{(l)})^2$ 如果我们不考虑后面一项，则式子变成了我们最开始的逻辑回归的代价函数，而我们用cost(i)= $y^{(i)}logh_{\Theta }(x^{(i)})+(1-y^{(i)})log(1-h_{\Theta }(x^{(i)}))$ ，认为

cost(i) $\approx$ $(h_{\Theta }(x^{(i)})-y^{(i)})^2$ ，所以我们仍然在做的是怎样使预测出来的值更接近实际数据，使所有距离之和最小。而我们的Backpropagation的整个计算流程如图3所示.

图3 Backpropagation

在图3中，首先我们的偏置单元是没有误差的，在这里 $\delta _{j}^{(l)}$ 来表示关于 $a_{j}^{(l)}$ 的误差。而 $\delta _{j}^{(l)}$ 的正式定义是 $\delta _{j}^{(l)}=\frac{\partial }{\partial z_{j}^{(l)}}cost(i)$ (cost(i)= $y^{(i)}logh_{\Theta }(x^{(i)})+(1-y^{(i)})log(1-h_{\Theta }(x^{(i)}))$ )，例如这里的 $\delta _{1}^{(4)}=a_{1}^{(4)}-y^{(i)}$ ，而 $\delta _{2}^{(3)}=\Theta _{12}^{(3)}\delta _{1}^{(4)}$ ， $\delta _{2}^{(2)}=\Theta _{12}^{(2)}\delta _{1}^{(3)}+\Theta _{22}^{(2)}\delta _{2}^{(3)}$ 等等，就是一个和正向传播一样，只是方向和传播的对象不同而已。

6.4 为后面算法的实现做些准备

在前面列写CostFunction时，我们给出函数的形式是这样的：

function [jVal,gradient]=costFunction(theta)

...

optTheta=fminunc(@costFunction,initialTheta,options)

在这里的theta和initialTheta告诉的都是一个向量而不是一个矩阵，而我们对于一个L=4的神经网络， $\Theta ^{(1)},\Theta ^{(2)},\Theta ^{(3)}$ 我们需要得到对应的矩阵( $\Theta$ 1, $\Theta$ 2, $\Theta$ 3)还有 $D^{(1)},D^{(2)},D^{(3)}$ 我们需要的也是对应的矩阵(D1,D2,D3)。

所以例如s1=10，s2=10，s3=1，

$\Theta ^{(1)}\in R^{10\times 11}$ ， $\Theta ^{(2)}\in R^{10\times 11}$ ， $\Theta ^{(3)}\in R^{1\times 11}$

$D ^{(1)}\in R^{10\times 11}$ ， $D ^{(2)}\in R^{10\times 11}$ ， $D ^{(3)}\in R^{1\times 11}$

thetaVec=[Theta1(:);Theta2(:);Theta3(:)]; %三个矩阵排成一个向量

DVec=[D1(:);D2(:);D3(:)];

Theta1=reshape(thetaVec(1:110),10,11); %把一个向量重新分成三个矩阵

Theta2 = reshape(thetaVec(111:220),10,11);

Theta3 = reshape(thetaVec(221:231),1,11);

所以对于所给的条件原始参数 $\Theta ^{(1)},\Theta ^{(2)},\Theta ^{(3)}$ ，需要通过展开得到一个向量initialTheta，然后再带入到函数fminunc(@costFunction, initialTheta, options)，而我们在构造costFunction函数时，是function [jval, gradientVec] = costFunction(thetaVec)，传进来的参数是thetaVec，这个时候我们则需要根据thetaVec得到 $\Theta ^{(1)},\Theta ^{(2)},\Theta ^{(3)}$ ，从而计算出 $D ^{(1)},D ^{(2)},D ^{(3)}$ ，然后通过展开成一个向量gradientVec。

6.5 Gradient checking(梯度算法的检验)

这个梯度算法看似很好，效率很高，但是我们不能确定这个算法是否正确，所以在这里我们给大家介绍一个另外来计算梯度的方法，这个同样也是梯度的定义，如图4所示，在图中我们可以看到，我们在曲线上任意选取一点 $\Theta$ ，做出该点的切线，切线的斜率即该点的真正梯度，而我们在该点的左右各选取一点 $\Theta -\varepsilon ,\Theta +\varepsilon$ ，两点之间的直线斜率即两点的纵坐标之差除以横坐标之差，如图所示，我们用公式表示出两点之间直线的斜率： $\frac{J(\Theta +\varepsilon )-J(\Theta -\varepsilon )}{2\varepsilon }$ ，而我们在 $\Theta$ 的梯度近似可以表示成 $\frac{J(\Theta +\varepsilon )-J(\Theta -\varepsilon )}{2\varepsilon }$ ，当 $\varepsilon$ 很小时，通常我们取 $\varepsilon$ 大概为 $10^{-4}$ 就可以了。

图4 梯度的定义

所以当我们 $\theta \in R^{n}$ ( $\theta$ 是 $\Theta ^{(1)},\Theta ^{(2)},\Theta ^{(3)}$ 展开后的一个向量)， $\theta =\theta _{1},\theta _{2},...,\theta _{n}$ 则

$\frac{\partial }{\partial \theta _{1}}J(\theta )\approx \frac{J(\theta _{1}+\varepsilon ,\theta _{2},...,\theta _{n})-J(\theta _{1}-\varepsilon ,\theta _{2},...,\theta _{n})}{2\varepsilon }$

...

$\frac{\partial }{\partial \theta _{n}}J(\theta )\approx \frac{J(\theta _{1} ,\theta _{2},...,\theta _{n}+\varepsilon)-J(\theta _{1} ,\theta _{2},...,\theta _{n}-\varepsilon)}{2\varepsilon }$

有一点值得注意的是，梯度检验算法计算量很大，效率不是很高，所以当我们检验了之前的梯度算法没问题后，一定要把梯度检验算法关掉，不然整个算法会运行很慢。

6.6 Random initialization(随机初始化)

这是这章的最后一个问题，在前面我们给大家介绍optTheta = fminunc(@costFunction,initialTheta, options)时，我们对initialTheta的处理一直是初始化为0，即initialTheta=zeros(n,1)，那么在这里我们是不是也需要进行同样的操作了？首先来看看如果我们初始化为0会有怎样的后果，如图5所示的一个神经网络模型。

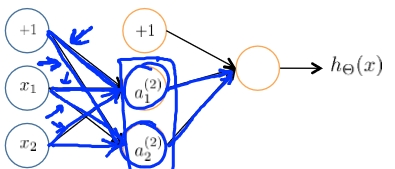
图5 一个3层的神经网络

在这个模型中，如果我们初始化令 $\Theta _{ij}^{l}=0$ ，则我们得到的 $a_{1}^{(2)}=a_{2}^{(2)}$ ，同样 $\delta _{1}^{(2)}=\delta _{2}^{(2)}$ ，则将会有 $\frac{\partial }{\partial \Theta _{01}^{(1)}}J(\Theta )=\frac{\partial }{\partial \Theta _{02}^{(1)}}J(\Theta )$ ， $\Theta _{01}^{(1)}=\Theta _{02}^{(1)}$ ，这样继续下去两者一直相等，所以是不对的，在这里我们要对 $\Theta _{ij}^{l}$ 进行随机化，让随机化的值都在[ $-\varepsilon ,\varepsilon$ ]内，则Theta1 = rand(10,11)*(2*INIT_EPSILON) - INIT_EPSILON;Theta2 = rand(1,11)*(2*INIT_EPSILON) - INIT_EPSILON;原本rand是使结果在(0,1)之间，现在我们是在(-INIT_EPSILON,INIT_EPSILON)之间。