监督学习中，如果预测的变量是离散的，我们称其为分类（如决策树，支持向量机等），如果预测的变量是连续的，我们称其为回归。回归分析中，如果只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。对于二维空间线性是一条直线；对于三维空间线性是一个平面，对于多维空间线性是一个超平面...这里，谈一谈最简单的一元线性回归模型。
1.一元线性回归模型
模型如下：
总体回归函数中Y与X的关系可是线性的，也可是非线性的。对线性回归模型的“线性”有两种解释：
（1）就变量而言是线性的，Y的条件均值是 X的线性函数
（2）就参数而言是线性的，Y的条件均值是参数
的线性函数
线性回归模型主要指就参数而言是“线性”,因为只要对参数而言是线性的,都可以用类似的方法估计其参数。
2.参数估计——最小二乘法
对于一元线性回归模型, 假设从总体中获取了n组观察值（X1，Y1），（X2，Y2）， …，（Xn，Yn）。对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小。有以下三个标准可以选择：
（1）用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
（2）用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
（3）最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外，得到的估计量还具有优良特性。这种方法对异常值非常敏感。
最常用的是普通最小二乘法（ Ordinary Least Square，OLS）：所选择的回归模型应该使所有观察值的残差平方和达到最小。（Q为残差平方和）
样本回归模型：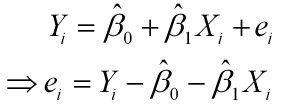
残差平方和：
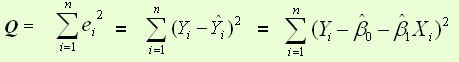
则通过Q最小确定这条直线，即确定
，以为变量，把它们看作是Q的函数，就变成了一个求极值的问题，可以通过求导数得到。求Q对两个待估参数的偏导数：
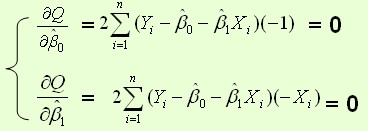
解得：
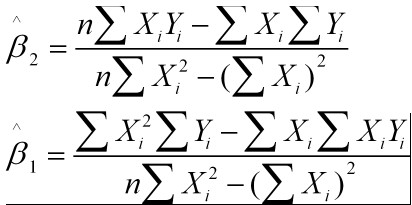
3.最小二乘法Python实现
# -*- coding: utf-8 -*-
#作者:kemp
import numpy as np #惯例
import scipy as sp #惯例
from scipy.optimize import leastsq #这里就是我们要使用的最小二乘的函数
import pylab as pl
m = 9 #多项式的次数
def real_func(x):
return np.sin(2*np.pi*x) #sin(2 pi x)
def fake_func(p, x):
f = np.poly1d(p) #多项式分布的函数
return f(x)
#残差函数
def residuals(p, y, x):
return y - fake_func(p, x)
#随机选了9个点，作为x
x = np.linspace(0, 1, 9)
#画图的时候需要的“连续”的很多个点
x_show = np.linspace(0, 1, 1000)
y0 = real_func(x)
#加入正态分布噪音后的y
y1 = [np.random.normal(0, 0.1) + y for y in y0]
#先随机产生一组多项式分布的参数
p0 = np.random.randn(m)
plsq = leastsq(residuals, p0, args=(y1, x))
print('Fitting Parameters ：', plsq[0]) #输出拟合参数
pl.plot(x_show, real_func(x_show), label='real')
pl.plot(x_show, fake_func(plsq[0], x_show), label='fitted curve')
pl.plot(x, y1, 'bo', label='with noise')
pl.legend()
pl.show()输出的拟合参数为：
Fitting Parameters ： [ 4.28790975e+03 -1.61487431e+04 2.44112227e+04 -1.89400574e+04
8.01662042e+03 -1.80367008e+03 1.75692385e+02 1.10072187e+00
-1.41404201e-02]
输出的图像为：
然后很明显，绿色的线过拟合了。有心的读者应该早就发现了，以上例子是Pattern Reconnition and Machine Learning上的例子。看过这本书的人都应该还记得，接下来我们应该是要加上penalty term来控制过拟合的情况。误差函数变为了：
这个时候我们只需要改变下残差函数就行了：
def residuals(p, y, x):
ret = y - fake_func(p, x)
ret = np.append(ret, np.sqrt(regularization)*p) #将lambda^(1/2)p加在了返回的array的后面
return ret设置好正则化系数后，图右：
