矩阵论

一、线性空间与线性变换

1 线性空间

涉及两个概念，集合与数域
数域 在抽象代数中，数域是指至少包含0和1的数集，在该集中进行数的和差积商的运算是封闭的
线性空间定义： 设 $V$是一个非空集合，其中的元素称为向量，F是数域，其中的数称为纯量。

1. 在 $V$中定义一种运算，称为加法，使得对任意的向量 $\alpha,\beta \in V$，有 $\alpha+\beta\in V$
2. 在 $P$与 $V$的元素间定义了一种运算，称为纯量乘法(亦称数量乘法)，即对 $V$中任意元素 $\alpha$和 $P$中任意元素 $k$，都按某一法则对应 $V$内惟一确定的一个元素 $k\alpha$，称为 $k$与 $\alpha$的积
3. 加法满足以下四个条件：

• 交换律
• 结合律
• 存在零向量0 $\in V$， $\forall\alpha\in V$, $\exists \alpha_0 \in V$使得 $\alpha+\alpha_0=\alpha$，记 $\alpha_0=$0
• 负元素存在 $\forall\alpha\in V$, $\exists \beta \in V$，使得 $\alpha+\beta=$0，记 $\beta=-\alpha$

4. 数量乘法满足以下四个条件

• 结合律
• 分配率（此处两个）
• $1·\alpha=\alpha$
  　　此时称 $V$是数域F上的线性空间

2 子空间

设 $W$是线性空间 $V_n(F)$的非空集合，则 $W$是 $V_n(F)$的子空间的充要条件是：

1. 若 $\alpha,\beta\in W$，则 $\alpha+\beta\in W$
2. 若 $\alpha\in W,k\in F$，则 $k\alpha\in W$

3 内积空间

定义了内积的线性空间

4 同一空间上的线性变换

 　　设 $V_n(F)$是一个线性空间，若有 $V_n(F)$上的对应关系 $T$，使 $\forall \alpha \in V_n(F)$都有确定的向量 $\alpha^{'}=T(\alpha)\in V_n(F)$与之对应，则称 $T$为 $V_n(F)$上一个变换，如果 $T$对加法和数乘封闭，则称称 $T$为 $V_n(F)$上一个线性变换

5 线性空间 $V_n(F)$到线性空间 $V_m(F)$的线性变换

6 线性空间的同构

映射

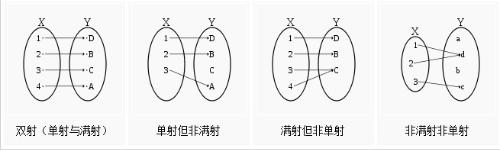
• 单射(injection):每一个x都有唯一的y与之对应
• 满射(surjection):每一个y都必有至少一个x与之对应
• 双射(又叫一一对应,bijection): 同时满足单射与满射，也就是常见的函数映射
  

二、矩阵的标准形

1 Jordan标准形

形如
$J(\lambda)=\begin{bmatrix}{\lambda}&{1}&{}&{}\\{}&{\lambda}&{1}&{}\\{}&{}&{\ddots}&{1}\\{}&{}&{}&{\lambda}\end{bmatrix}$
的 $r$阶方阵成为一个 $r$阶Jordan块，其中 $\lambda$可以是实数，也可以是复数。由若干个Jordan块 $J_i(\lambda_i)$构成的准对角矩阵
$J=\begin{bmatrix}{J_1(\lambda_1)}&{}&{}&{}\\{}&{J_2(\lambda_2)}&{}&{}\\{}&{}&{\ddots}&{}\\{}&{}&{}&{J_m(\lambda_m)}\end{bmatrix}$
称为Jordan矩阵
定理： 在复数域上，每个n阶方阵A都相似于一个Jordan矩阵，即存在可逆矩阵P，使得
$P^{-1}AP=J_A$
求Jordan标准形： 借助于Smith标准形，初等因子
 　　通过初等变换化A的特征矩阵 $\lambda E-A$为Smith标准形，求出不变因式后，再计算出初等因子，就可以得到与n阶矩阵A相似的Jordan标准形。

2 化零多项式与最小多项式

解决A的矩阵多项式的问题

三、矩阵分解

1 三角分解LU、LDV

借助于高斯消元法实现，用途主要在简化一个大矩阵的行列式值的计算过程，求逆矩阵，和求解联立方程组，分解不唯一

2 满秩分解

分解不唯一

3 谱分解

4 SVD分解

SVD分解法的用途是解最小平方误差法和数据压缩

四、矩阵的广义逆

五、矩阵分析