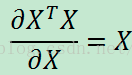http://blog.csdn.net/pipisorry/article/details/68961388

复杂的矩阵函数求导。著名的matrix cookbook为广大的研究者们提供了一本大字典，里面有着各种简单到复杂矩阵和向量的求导法则。

布局(Layout)

矩阵求导有两种布局，分子布局(numerator layout)和分母布局(denominator layout)。

为了阐明这两种布局的区别，我们先来看最简单的求导规则。

首先是向量 $y$ 对标量 $x$ 求导，我们假定所有的向量都是列向量，

y = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ y 1 y 2 ⋮ y m ⎤ ⎦ ⎥ ⎥ ⎥ ⎥

在分子布局下，

\partial y \partial x = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ \partial y 1 \partial x \partial y 2 \partial x ⋮ \partial y m \partial x ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥

而在分母布局下，

\partial y \partial x = [\partial y 1 \partial x \partial y 2 \partial x \dots \partial y m \partial x]

你可以随时在两种布局间进行转换，只要你自己不犯迷糊。

向量求导规则

基本的求导规则

标量函数关于向量的导数

定义：若 $f$ 是 $\mathbb{R}^n$ 中向量 $\textbf{X}=(x_1,x_2,\cdot\cdot\cdot,x_n)^T$ 的数量函数 $f(\textbf{X})$ ，则 $f$ 对 $\textbf{X}$ 的导数（即数量函数 $f$ 的梯度）为

$\frac{df}{d\textbf{X}}=(\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\cdot\cdot\cdot,\frac{\partial f}{\partial x_n})^T$

在此，数量函数是指函数 $f$ 的输出是标量。由以上定义可知，我们所说的对向量的导数是函数关于向量元素的偏导数。因此，得到的导数结果是一向量，与向量 $\textbf{X}$ 的维度一致。

标量函数关于矩阵的导数

本质上，向量就是矩阵，如果理解了数量函数关于向量的导数，就不难理解数量函数关于矩阵的导数。

标量 y 对向量 x 求导

\partial y \partial x = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ \partial y \partial x 1 \partial y \partial x 2 ⋮ \partial y \partial x m ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥

注意到，标量对向量求导和向量对标量求导刚好反过来。

向量对向量求导，

x = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ x 1 x 2 ⋮ x n ⎤ ⎦ ⎥ ⎥ ⎥ ⎥

y = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ y 1 y 2 ⋮ y m ⎤ ⎦ ⎥ ⎥ ⎥ ⎥

\partial y \partial x = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ \partial y 1 \partial x 1 \partial y 1 \partial x 2 ⋮ \partial y 1 \partial x n \partial y 2 \partial x 1 \partial y 2 \partial x 2 ⋮ \partial y 2 \partial x n \dots \dots ⋱ \dots \partial y m \partial x 1 \partial y m \partial x 2 ⋮ \partial y m \partial x n ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥

标量对矩阵求导，

\partial y \partial X = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ \partial y \partial x 11 \partial y \partial x 21 ⋮ \partial y \partial x p 1 \partial y \partial x 12 \partial y \partial x 22 ⋮ \partial y \partial x p 2 \dots \dots ⋱ \dots \partial y \partial x 1 q \partial y \partial x 2 q ⋮ \partial y \partial x p q ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥

矩阵对标量求导，

\partial y \partial x = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ \partial y 11 \partial x \partial y 12 \partial x ⋮ \partial y 1 n \partial x \partial y 21 \partial x \partial y 22 \partial x ⋮ \partial y 2 n \partial x \dots \dots ⋱ \dots \partial y m 1 \partial x \partial y m 2 \partial x ⋮ \partial y m n \partial x ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥

事实上，直观上看，凡是对标量求导，结果的形式都要转置，而标量对向量和矩阵求导则位置保持不动。这样总结方便我们记忆。

总的来说，涉及矩阵和向量的求导不外乎五大类别，

向量对标量
标量对向量
向量对向量
矩阵对标量
标量对矩阵

常用向量求导公式：实值标量函数对向量x的偏导

机器学习中常用的矩阵求导公式

Y = A * X --> DY/DX = A'
Y = X * A --> DY/DX = A
Y = A' * X * B --> DY/DX = A * B'
Y = A' * X' * B --> DY/DX = B * A'

皮皮blog

向量求导的示例

逐项展开分析

向量求导与标量求导法则不同的是，向量的求导还要注意结果的排法问题。注意排法是因为当一个目标函数是多个成分相加时，如果不注意排法可能导致有些结果是行，有些是列，无法继续进行运算。我总结的向量求导的基本推导准则是（以f(x)对向量 $x = (x_1,...,x_n)^T$ 求导为例）：

1）先对f(x)求向量分量的导数，也就是标量 $x_i$ 的导数，该导数可能是标量，也可能是向量;

2）如果第一步求导结果为标量，直接将结果排列成x的形状(本例为列)；如果第一步求出的结果是向量，在按照x排列结果时：

　　2.1）如果求导结果与x形状相同，则将结果取转置排成矩阵;

　　2.3）如果求导结果与x形状不同，则直接将结果排成矩阵。

两个例子

以下约定向量x是列向量, $A = [a_1,a_2,...,a_n]$ 是矩阵， $，A^T = [a'_1,...,a'_n]$ 是A的转置。

例1

1）求分量导数 $\frac{\partial(Ax)}{\partial x_k} = \frac{\partial \sum_ia_ix_i}{\partial x_k} = a_k$

2.1)排列：求导结果与x形状相同，将 $a_k$ 取转置按列排好，即A的转置： $\frac{\partial Ax}{\partial x} = A^T$

例2

[矩阵分析与应用-张贤达]

2)上述结果是标量，直接排成一列，整理一下得： $\frac{\partial x^TAx}{\partial x} = (A + A^T)x$

有了基本求导规则，就可以求一些更复杂基本函数的导数。对于矩阵的行列式，向量的叉积，矩阵的逆这些更复杂的导数的求法以及向量的链式求导规则，下篇再表。

如果变量是矩阵，上述法则是很容易推广到矩阵上去的：矩阵是由向量组成的，先利用上述向量的求导法则求导，再对结果进行排列，排列的讨论与2)非常类似。

示例3

首先是 $\frac{\partial A x}{\partial x}$ ,注意到 $(A x)_{i} = a_{i 1} x_{1} + a_{i 2} x_{2} + \dots + a_{i n} x_{n}$ ,于是利用向量对向量求导法则，我们有

\partial A x ) \partial x = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ \partial ( A x ) 1 \partial x 1 \partial ( A x ) 1 \partial x 2 ⋮ \partial ( A x ) 1 \partial x n \partial ( A x ) 2 \partial x 1 \partial ( A x ) 2 \partial x 2 ⋮ \partial ( A x ) 2 \partial x n \dots \dots ⋱ \dots \partial ( A x ) m \partial x 1 \partial ( A x ) m \partial x 2 ⋮ \partial ( A x ) m \partial x n ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ a 11 a 12 ⋮ a 1 n a 21 a 22 ⋮ a 2 n \dots \dots ⋱ \dots a m 1 a m 2 ⋮ a m n ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ = A T

理论上对于任意的表达式，我们都可以通过定义出发，利用上面这种形式推导得到。

但是对于一些复杂的求导，这个时候恐怕逐项展开分析就不是很靠谱了。

维度分析

考虑

\frac{\partial A u}{\partial x}

A

与

x

无关，所以

A

肯定可以先提出求导式，至于去哪了暂时不清楚。

假如 $A \in R^{m \times n}, u \in R^{n \times 1}, x \in R^{p \times 1}$ ,我们知道最后结果肯定和 $\frac{\partial u}{\partial x}$ 有关，注意到 $\frac{\partial u}{\partial x} \in R^{p \times n}$ ,于是 $A$ 只能转置以后添在后面，因此

\partial A u \partial x = \partial u \partial x A T

同样对于 $\frac{\partial a u}{\partial x}, a$ 和 $x$ 相关的标量，假定 $u \in R^{m \times 1}, x \in R^{n \times 1}$ ,根据乘积法则（非精确版本），前一个部分肯定是 $a \frac{\partial u}{\partial x}$ ,后一部分为 $\frac{\partial a}{\partial x} \in R^{n \times 1}$ 和 $u$ 的某种形式的积,分析维度发现只能是 $\frac{\partial a}{\partial x} u^{T}$ 。于是

\partial a u \partial x = a \partial u \partial x + \partial a \partial x u T

我们发现，虽然乘积法则的精准形式无法应用于矩阵求导中，然而这种非精确的乘积法则可以准确的告诉我们哪些项一定会出现在结果中，然后通过分析维度，我们就可以写出结果。再看 $\frac{\partial x^{T} A x}{\partial x}$ ,其中 $A$ 和 $x$ 无关，为了分析这个问题，我们考虑一个更一般的问题，

\partial x T A y \partial x, x \in ℝ m \times 1, y \in ℝ n \times 1

我们利用非精确的乘积法则，可以将这个分成两部分

\partial ( x T A ) y \partial x

于是结果和两部分相关，一个是 $\frac{\partial y}{\partial x} \in R^{m \times n}$ ,另一个是 $\frac{\partial x^{T} A}{\partial x} = A \in R^{m \times n}$ ,同样通过分析维度，我们可以得到

\partial ( x T A ) y \partial x = \partial y \partial x A T x + A y

因此

\partial x T A x \partial x = (A T + A) x

最后看一个式子

\partial a T x x T b \partial x, a, b, x \in ℝ m \times 1

\partial a T x x T b \partial x = \partial ( a T x ) ( x T b ) \partial x

注意到

\partial ( a T x ) \partial x = a, \partial ( x T b ) \partial x = b

所以(注意到 $x^{T} b \in R$ )

\partial a T x x T b \partial x = \partial ( a T x ) ( x T b ) \partial x = a x T b + b a T x = (a b T + b a T) x

皮皮blog

矩阵求导整理

1. 矩阵Y对标量x求导：

相当于每个元素求导数后转置一下，注意M×N矩阵求导后变成N×M了

Y = [y(ij)]--> dY/dx = [dy(ji)/dx]

2. 标量y对列向量X求导：

注意与上面不同，这次括号内是求偏导，不转置，对N×1向量求导后还是N×1向量

y = f(x1,x2,..,xn)--> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)'

3. 行向量Y'对列向量X求导：

注意1×M向量对N×1向量求导后是N×M矩阵。

将Y的每一列对X求偏导，将各列构成一个矩阵。

重要结论：

dX'/dX = I

d(AX)'/dX = A'

4. 列向量Y对行向量X’求导：

转化为行向量Y’对列向量X的导数，然后转置。

注意M×1向量对1×N向量求导结果为M×N矩阵。

dY/dX' = (dY'/dX)'

5. 向量积对列向量X求导运算法则：

注意与标量求导有点不同。

d(UV')/dX = (dU/dX)V' +U(dV'/dX)

d(U'V)/dX = (dU'/dX)V +(dV'/dX)U'

重要结论：

d(X'A)/dX = (dX'/dX)A +(dA/dX)X' = IA + 0X' = A

d(AX)/dX' = (d(X'A')/dX)' =(A')' = A

d(X'AX)/dX = (dX'/dX)AX +(d(AX)'/dX)X = AX + A'X

6. 矩阵Y对列向量X求导：

将Y对X的每一个分量求偏导，构成一个超向量。

注意该向量的每一个元素都是一个矩阵。

7. 矩阵积对列向量求导法则：

d(uV)/dX = (du/dX)V +u(dV/dX)

d(UV)/dX = (dU/dX)V +U(dV/dX)

重要结论：

d(X'A)/dX = (dX'/dX)A +X'(dA/dX) = IA + X'0 = A

8. 标量y对矩阵X的导数：

类似标量y对列向量X的导数，

把y对每个X的元素求偏导，不用转置。

dy/dX = [ Dy/Dx(ij) ]

重要结论：

y = U'XV = ΣΣu(i)x(ij)v(j)于是 dy/dX = [u(i)v(j)] = UV'

y = U'X'XU 则 dy/dX =2XUU'

y = (XU-V)'(XU-V) 则 dy/dX =d(U'X'XU - 2V'XU + V'V)/dX = 2XUU' - 2VU' + 0 = 2(XU-V)U'

9. 矩阵Y对矩阵X的导数：

将Y的每个元素对X求导，然后排在一起形成超级矩阵。

from: http://blog.csdn.net/pipisorry/article/details/68961388

ref: [刘丁酉《矩阵分析》]

[闲话矩阵求导]*

矩阵论：向量求导/微分和矩阵微分

布局(Layout)

向量求导规则

标量函数关于向量的导数

标量函数关于矩阵的导数

标量 y 对向量 x 求导

常用向量求导公式：实值标量函数对向量x的偏导

向量求导的示例

逐项展开分析

两个例子

示例3

维度分析

矩阵求导整理

猜你喜欢