动态规划
斐波那契数列:
边界条件:f0=0;
f1=1;
能够直接被求出值的状态
不需要计算其他斐波那契数列的值直接可以得到结果;
转移方程:fn=fn-1+fn-2如何用已有状态求出未知状态
前几项:0,1,1,2,3,5,8,13……
状态:f1,f2,f3……fn;(要求的未知的量)
DAGó无后效性??(暂时不用管什么东西)
通项公式:

法1:记忆化搜索(一般来说用不上qwq)
会多开一个记录是否算过的数组,故空间会比下面两种大一点
法2:顺着推:用自己去推别人
法3:倒着推:用别人更新自己
#include<iostream> #include<cstdio> using namspace std; int n,f[233]; /*斐波那契数列:倒着推 int main(){ cin>>n; f[0]=0; f[1]=1; for(int a=2;a<n;a++) { f[a]=f[a-1]+f[a-2]; } cout<<f[n]<<endl; }*/ /*斐波那契数列:顺着推 int main(){ cin>>n; f[0]=0; f[1]=1; for(int a=0;a<n;a++){ f[a+1]+=f[a]; f[a+2]+=f[a]; } cout<<f[n]<<endl; } */ /*搜索 O(f(n)) 与斐波那契数列第n项大小成正比 约为1.6^n int dfs(int n){ if(n==0) return 0; if(n==1) return 1; return dfs(n-1)+dfs(n-2); } int main(){ cin>>n; cout<<dfs(n)<<endl; return 0 } */ /*记忆化搜索 O(n) 在计算过程中,保证f0~fn每个数只被算一次 bool suan_le_mei[n]; int dfs(int n){ if(n==0) return 0; if(n==1) return 1; if(suan_le_mei[n]) return f[n];//判断是否算过 suan_le_mei[n]=true; f[n]=dfs(n-1)+dfs(n-2); return f[n]; } int main(){ cin>>n; cout<<dfs(n)<<endl; return 0 }*/
矩阵优化(O(logn))
常见DP种类
数位DP
树形DP
状压DP
区间DP
(有套路^)
其他DP(可能性很大)无规律
考不到的DP:插头DP,博弈论DP,呸概率比较小
数位DP
什么叫做数位DP?
读入两个正整数l,r,问从l~r有多少个数?
ans=r-l+1;
第一步:转化:[0,r]数的个数-[0,l-1]的数的个数=>转化成解决[0,x]有多少数=>有多少个v使得0<=v<=x;
x=>xn xn-1 xn-2……x0
v=>vn vn-1vn-2……v0(至多n位)给每位填上0~9的数,看有多少种方案满足v<=x

从最高位=>最低位,那么填vn-3时,前面的都填好了
那么v的前面的三位必须保证小于等于x的前三位,那么为了使v<=x,则需要:
分两种情况:1.x的前三位大于v的前三位=>vn-3可以填任何数
2.x的前三位等于v的前三位=>0~xn-3
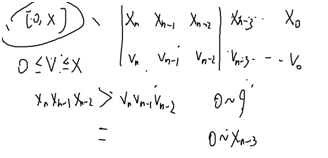
f[i][j(0/1)] 代表这种情况的方案数
i:已经填好了第i位,j=>0/1
j=0 xnxn-1……xi>vnvn-1……vi;
j=1 xnxn-1……xi=vnvn-1……vi;
转移:枚举第i-1位填什么
填第i位,从i+1位转移过来.
边界:第n+1位(相等且没有数)f[n+1][1]=1;(都填0)

#include<iostream> using namespace std; int l,r,z[233]; int f[2333][2]; int solve(int x){ int n=0; while(x){//求出x的每一位(最后有n位)(从0下标开始) z[n]=x%10; x/=10; n++; } n--; memset(f,0,sizeof(f));//需要做两次DP,故要把数组清空 f[n+1][1]=1;//边界条件:第n+1位显然都填0,所以相等的方案数为1 //不相等的方案数为0 for(int a=n;a>=0;a--)//枚举要填的第a位 { for(int b=0;b<=1;b++)//考虑相等还是小于分两种讨论qwq if(b==0){//x>v for(int c=0;c<=9;c++) f[a][0]+=f[a+1][b]; } else { for(int c=0;c<=z[a];c++){ if(c==z[a])f[a][1]+=f[a+1][b]//c==z[a],代表填上这个数后v=x else f[a][0]+=f[a+1][b];//c!=z[a],代表填上这个数后v<x } } } return f[0][0]+f[0][1]; } int main(){ cin>>l>>r; cout<<solve(r)-solve(l-1)<<endl; return 0; }
problem2:
求[l,r]中的数的数位之和
#include<iostream> #include<cstring> using namespace std; int l,r,z[233]; int f[2333][2]; int g[2333][2];//ij表达与f相同 int solve(int x){ int n=0; while(x){//求出x的每一位(最后有n位)(从0下标开始) z[n]=x%10; x/=10; n++; } n--; memset(f,0,sizeof(f));//需要做两次DP,故要把数组清空 memset(g,0,sizeof(g)); f[n+1][1]=1;//边界条件:第n+1位显然都填0,所以相等的方案数为1,不相等的方案数为0 g[n+1][1]=0; for(int a=n;a>=0;a--)//枚举要填的第a位 { for(int b=0;b<=1;b++)//考虑相等还是小于分两种讨论qwq if(b==0){//x>v for(int c=0;c<=9;c++){ f[a][0]+=f[a+1][b]; g[a][0]+=g[a+1][b]+f[a+1][b]*c;//先加上前a+1位的和,然后对于第a位,可以填0~9任一,那么每填一个数c,每一种方案的和都+c,故要用方案数*c } } else { for(int c=0;c<=z[a];c++){ if(c==z[a]){ f[a][1]+=f[a+1][b]; g[a][1]+=g[a+1][b]+f[a+1][b]*c; }//c==z[a],代表填上这个数后v=x else { f[a][0]+=f[a+1][b];//c!=z[a],代表填上这个数后v<x g[a][0]+=g[a+1][b]+f[a+1][b]*c; } } } } //return f[0][0]+f[0][1]; return g[0][0]+g[0][1]; } int main(){ cin>>l>>r; cout<<solve(r)-solve(l-1)<<endl; return 0; }
problem3:
求在[l,r]中的满足相邻两个数字之差至少为2的数有多少个
多一维条件,多一个状态。
f[i][j][k]已经填好了第i位;j</=;k:第i位填了k
保证第i位和第i+1位的数字大小差至少2;
数位-50%
树形-50%
区间-50%
状压-50%
其他-80%
树形DP:
给你一个n个点的数,问有多少个点???闲圈啊qwq
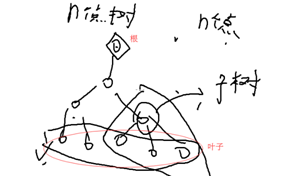
f[i]以i为根的子树中共有多少个点
边界条件:叶节点的f为1;f[叶子]=1;
f[p]=f[p1]+f[p2]+1;
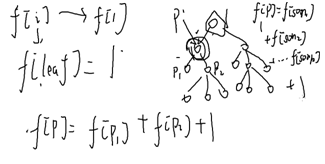
转移方程 f[i]=f[son1]+f[son2]+……+f[sonn]+1
eg:
给我一个n个点的数,求这棵树的直径是多少?
直径:在一棵树上找到两个点,使得这两点间的距离最远。
考虑一棵子树内的直径qwq
路径长这样:
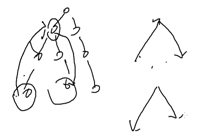
可以把直径看成从某一点向下走了两条路然后合起来
找两种向下走最长的两条路径
即从一点向下走最长可以走多少和次长可以走多少。
状态定义:f[i][0]i向下最长那条路长度是多少
f[i][1]i乡下的次长的那条路的长度
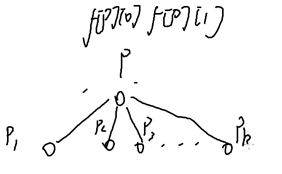
转移方程:(n个儿子)
f[p][0]=max(f[son1][0],f[son2][0]……,f[sonn][0])+1;
假设最大的是son2,那么显然我们不能再走son2了
f[p][1]=max(f[son1][0],f[son3][0],……f[sonn][0])+1;
ans=max(f[i][0]+f[i][1])-1吧???;(枚举所有的i找最大的一个)
