【图像特征提取（一）边缘特征之Sobel】

版权声明：本文为博主原创文章，转载时须注明出处 https://blog.csdn.net/KID_yuan/article/details/88566392

什么是图像特征：

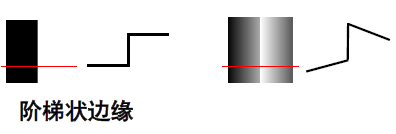
图像特征 ：个人觉得能够刻画从一副图像的大致内容信息的图像中的一部分就是图像的特征。比如：
亮度，纹理，边缘，角点，特征描述子和区域等等都可以作为描述图像信息的一部分。

---

图像边缘：
物体的边界，表面方向的改变，不同的颜色，光照明暗的变化。

---

图像微分算子

一阶微分算子（梯度算子）：Roberts，Prewitt，，Sobel。

• 检测极大值
  一阶算子通常是通过计算返回水平Gx和垂直Gy方向的一阶导数值，由此便可以确定像素点的梯度G(x,y)和方向θ 。

二阶微分算子：Laplacian

• 检测过零点
  二阶算子通常是计算零点，证明其存在边缘（之后根据实际情况进行边缘取舍）。
  几种算子对比

Roberts算子

斜向偏差分的梯度计算方法，梯度幅值大小代表边缘的强度，梯度的方向与边缘方向垂直，实际上是求旋转±45°方向上两个微分值的和。
两个卷积核：
${G_x} = \left\lfloor \begin{array}{l} {\rm{1}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0\\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - 1 \end{array} \right\rfloor {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {G_y}{\rm{ = }}\left\lfloor \begin{array}{l} {\rm{0}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{1}}\\ {\rm{ - 1}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{0}} \end{array} \right\rfloor {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}$

梯度幅值与方向：
$\begin{array}{l} G(x,y) = \sqrt {G_x^2 + G_y^2} \\ \theta = \arctan ({G_y}/Gy) \end{array}$

通常将幅值近似： $|G(x,y)| = {\rm{|}}{{\rm{G}}_{\rm{x}}}{\rm{| + |}}{{\rm{G}}_{\rm{y}}}{\rm{|}}$

Prewitt算子

两个卷积核：权重相同的算子

${G_x} = \left\lfloor \begin{array}{l} - 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1\\- 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1\\ {\kern 1pt} - 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1 \end{array} \right\rfloor {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {G_y}{\rm{ = }}\left\lfloor \begin{array}{l} 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{1}}\\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{0}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{0}}\\ - 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - 1 \end{array} \right\rfloor {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}$
梯度幅值：
$G(x,y) \approx \max ({\rm{|}}{{\rm{G}}_{\rm{x}}}{\rm{|,|}}{{\rm{G}}_{\rm{y}}}{\rm{|}})$

Sobel算子

这个著名的Sobel边缘算子是一组方向算子，从不同的方向检测边缘。当年作者并没有公开发表过论文，仅仅是在一次博士生课题讨论会(1968)上提出(“A 3x3 Isotropic Gradient Operator for Image Processing”)，后在1973年出版的一本专著（“Pattern Classification and Scene Analysis”）的脚注里作为注释出现和公开的。Sobel算子不是简单的求平均差分，而是加强中心像素上下左右四个方向的权重，运算结果是一幅边缘图像。

${G_x} = \left\lfloor \begin{array}{l} - 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1\\- 2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2\\ {\kern 1pt} - 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1 \end{array} \right\rfloor {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {G_y}{\rm{ = }}\left\lfloor \begin{array}{l} 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{1}}\\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{0}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{0}}\\ - 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - 2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - 1 \end{array} \right\rfloor {\kern 1pt} {\kern 1pt}$

• 注：Gx水平算子，实际检测垂直方向上的边缘；Gy为垂直算子，实际检测水平方向的边缘。
• Sobel算子方向
  

---

梯度幅值与方向：
$\begin{array}{l} G(x,y) = \sqrt {G_x^2 + G_y^2} \\ \theta = \arctan ({G_y}/Gy) \end{array}$
通常将幅值近似： $|G(x,y) |= {\rm{|}}{{\rm{G}}_{\rm{x}}}{\rm{| + |}}{{\rm{G}}_{\rm{y}}}{\rm{|}}$

若图像中一个3x3的窗口为A，要计算梯度的像素点为P，则和Sobel算子进行卷积之后，像素点P在x和y方向的梯度值分别为：

参考博客： https://www.cnblogs.com/techyan1990/p/7291771.html