document.title="【Foundation of data science】Clustering"
Clustering ,翻译为"聚类",就是把相似的东西分为一组,同 Classification(分类)不同, classifier 从训练集中进行"学习",从而能够对未知数据进行分类,这种提供训练数据的过程叫做 supervised learning (监督学习),而在聚类的时候,我们并不关心某一类是什么,我们只需要把相似的东西聚到一起,因此,一个聚类算法通常只需要知道如何计算相似度就可以工作了,因此 clustering 通常并不需要使用训练数据进行学习,这在 Machine Learning 中被称作 unsupervised learning (无监督学习)。
Clustering ,翻译为"聚类",就是把相似的东西分为一组,同 Classification(分类)不同, classifier 从训练集中进行"学习",从而能够对未知数据进行分类,这种提供训练数据的过程叫做 supervised learning (监督学习),而在聚类的时候,我们并不关心某一类是什么,我们只需要把相似的东西聚到一起,因此,一个聚类算法通常只需要知道如何计算相似度就可以工作了,因此 clustering 通常并不需要使用训练数据进行学习,这在 Machine Learning 中被称作 unsupervised learning (无监督学习)。
## 一、聚类的两种常用的假设
### 1、基于中心的聚类(Center-based clusters)
### 1、基于中心的聚类(Center-based clusters)
1. **k-center clustering:** 最小化数据点到其中心的最大距离,即minimize
$$
\Phi_{k c e n t e r}(\mathcal{C})=\max _{j=1} \max _{\mathbf{a}_{i} \in C_{j}} d\left(\mathbf{a}_{i}, \mathbf{c}_{j}\right)
$$
例如,消防站位置问题(最小化消防站可能需要前往的最大距离)。
2. **k-median clustering:** 最小化数据点到其中心的距离之和,即minimize$$
\Phi_{k m e d i a n}(\mathcal{C})=\sum_{j=1}^{k} \sum_{\mathbf{a}_{i} \in C_{j}} d\left(\mathbf{a}_{i}, \mathbf{c}_{j}\right)
$$
k-median比k-center更具有抗噪性,因为少数异常值通常不会更改最佳解决方案。
3. **k-means clustering:** 最小化数据点到其中心的距离平方和,即mminimize$$
\Phi_{k m e a n s}(\mathcal{C})=\sum_{j=1}^{k} \sum_{\mathbf{a}_{i} \in C_{j}} d^{2}\left(\mathbf{a}_{i}, \mathbf{c}_{j}\right)
$$
k-means比k-median更重视异常值,因为对距离进行了平方,这会放大大的值。
$$
\Phi_{k c e n t e r}(\mathcal{C})=\max _{j=1} \max _{\mathbf{a}_{i} \in C_{j}} d\left(\mathbf{a}_{i}, \mathbf{c}_{j}\right)
$$
例如,消防站位置问题(最小化消防站可能需要前往的最大距离)。
2. **k-median clustering:** 最小化数据点到其中心的距离之和,即minimize$$
\Phi_{k m e d i a n}(\mathcal{C})=\sum_{j=1}^{k} \sum_{\mathbf{a}_{i} \in C_{j}} d\left(\mathbf{a}_{i}, \mathbf{c}_{j}\right)
$$
k-median比k-center更具有抗噪性,因为少数异常值通常不会更改最佳解决方案。
3. **k-means clustering:** 最小化数据点到其中心的距离平方和,即mminimize$$
\Phi_{k m e a n s}(\mathcal{C})=\sum_{j=1}^{k} \sum_{\mathbf{a}_{i} \in C_{j}} d^{2}\left(\mathbf{a}_{i}, \mathbf{c}_{j}\right)
$$
k-means比k-median更重视异常值,因为对距离进行了平方,这会放大大的值。
当数据由$R^d$中的点组成时,更常使用k-means准则,而当我们具有有限度量时,k-median更常用,即数据是具有边距离的图中的节点。
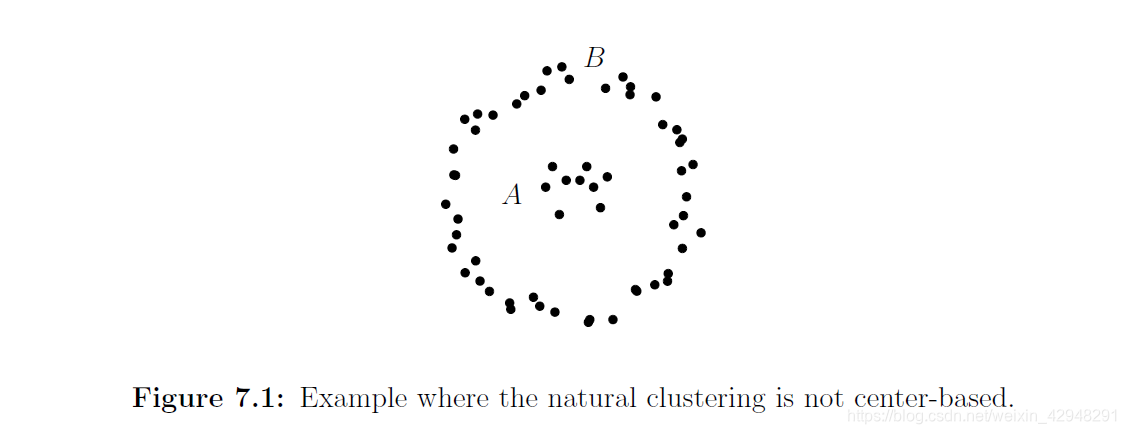
### 2、高密度聚类
如果我们不相信我们的聚类是基于中心的,那么通常做出的的另一个假设是聚类由高密度区域组成,他们之间是低密度的“护城河”。
## 二、k-Means Clustering
### 1、动机
考虑使用k-means准则的最大似然动机。假设我们的数据是由k个良好分离的球形高斯密度等权混合生成的,这k个高斯密度的均值分别为$\mathbf{\mu}_2, \mathbf{\mu}_2, \dots, \mathbf{\mu}_k$,方差都为1。从而混合分布的密度为$$
\operatorname{Prob}(\mathrm{x})=\frac{1}{(2 \pi)^{d / 2}} \frac{1}{k} \sum_{i=1}^{k} e^{-\left|\mathrm{x}-\mu_{i}\right|^{2}}
$$
定义最接近x的中心为$\mu(x)$,由于指数函数快速下降,我们可以用$e^{-|\mathbf{x}-\boldsymbol{\mu}(\mathbf{x})|^{2}}$近似$\sum_{i=1}^{k} e^{-\left|\mathbf{x}-\boldsymbol{\mu}_{i}\right|^{2}}$。因此,$$
\operatorname{Prob}(\mathbf{x}) \approx \frac{1}{(2 \pi)^{d / 2} k} e^{-|\mathbf{x}-\mu(\mathbf{x})|^{2}}
$$
从而,从混合分布中选择样本点的可能性为$$
\frac{1}{k^{n}} \frac{1}{(2 \pi)^{n d / 2}} \prod_{i=1}^{n} e^{-\left|\mathbf{x}^{(\mathrm{i})}-\mu\left(\mathrm{x}^{(\mathrm{i})}\right)\right|^{2}}=c e^{-\sum_{i=1}^{n}\left|\mathrm{x}^{(\mathrm{i})}-\mu\left(\mathrm{x}^{(\mathrm{i})}\right)\right|^{2}}
$$
因此,最小化到聚类中心的距离平方和得到最大似然 $\mathbf{\mu}_2, \mathbf{\mu}_2, \dots, \mathbf{\mu}_k$。
### 2、k-means目标的性质
**引理2.1** 当x是质心时,数据点到x的距离平方和得到最小化,即$\mathbf{x}=\frac{1}{n} \sum_{i} \mathbf{a}_{\mathbf{i}}$。
**证明**:我们的目标是寻找x,最小化$\sum_{i}\left|\mathbf{a}_{\mathbf{i}}-\mathbf{x}\right|^{2}$。通过简单计算可得
$$
\sum_{i}\left|\mathrm{a}_{\mathrm{i}}-\mathrm{x}\right|^{2}=\sum_{i}\left|\mathrm{a}_{\mathrm{i}}-\mathrm{c}\right|^{2}+n|\mathrm{c}-\mathrm{x}|^{2}
$$等式右边第一部分是确定的数,第二部分最小值为0,在$x=c$处取得。
### 3、Lloyd's Algorithm
k-means聚类一个常用的算法是Lloyd's Algorithm。
**Lloyd's Algorithm:**
1. 初始化k个中心(随机选择?);
2. 将每个点与最靠近它的中心聚类;
3. 找到每个聚类的质心作为新中心替换旧中心;
4. 重复Step 2和Step 3直到聚类中心收敛(根据一些准则,例如k-means得分不再提高)
### 2、高密度聚类
如果我们不相信我们的聚类是基于中心的,那么通常做出的的另一个假设是聚类由高密度区域组成,他们之间是低密度的“护城河”。

## 二、k-Means Clustering
### 1、动机
考虑使用k-means准则的最大似然动机。假设我们的数据是由k个良好分离的球形高斯密度等权混合生成的,这k个高斯密度的均值分别为$\mathbf{\mu}_2, \mathbf{\mu}_2, \dots, \mathbf{\mu}_k$,方差都为1。从而混合分布的密度为$$
\operatorname{Prob}(\mathrm{x})=\frac{1}{(2 \pi)^{d / 2}} \frac{1}{k} \sum_{i=1}^{k} e^{-\left|\mathrm{x}-\mu_{i}\right|^{2}}
$$
定义最接近x的中心为$\mu(x)$,由于指数函数快速下降,我们可以用$e^{-|\mathbf{x}-\boldsymbol{\mu}(\mathbf{x})|^{2}}$近似$\sum_{i=1}^{k} e^{-\left|\mathbf{x}-\boldsymbol{\mu}_{i}\right|^{2}}$。因此,$$
\operatorname{Prob}(\mathbf{x}) \approx \frac{1}{(2 \pi)^{d / 2} k} e^{-|\mathbf{x}-\mu(\mathbf{x})|^{2}}
$$
从而,从混合分布中选择样本点的可能性为$$
\frac{1}{k^{n}} \frac{1}{(2 \pi)^{n d / 2}} \prod_{i=1}^{n} e^{-\left|\mathbf{x}^{(\mathrm{i})}-\mu\left(\mathrm{x}^{(\mathrm{i})}\right)\right|^{2}}=c e^{-\sum_{i=1}^{n}\left|\mathrm{x}^{(\mathrm{i})}-\mu\left(\mathrm{x}^{(\mathrm{i})}\right)\right|^{2}}
$$
因此,最小化到聚类中心的距离平方和得到最大似然 $\mathbf{\mu}_2, \mathbf{\mu}_2, \dots, \mathbf{\mu}_k$。
### 2、k-means目标的性质
**引理2.1** 当x是质心时,数据点到x的距离平方和得到最小化,即$\mathbf{x}=\frac{1}{n} \sum_{i} \mathbf{a}_{\mathbf{i}}$。
**证明**:我们的目标是寻找x,最小化$\sum_{i}\left|\mathbf{a}_{\mathbf{i}}-\mathbf{x}\right|^{2}$。通过简单计算可得
$$
\sum_{i}\left|\mathrm{a}_{\mathrm{i}}-\mathrm{x}\right|^{2}=\sum_{i}\left|\mathrm{a}_{\mathrm{i}}-\mathrm{c}\right|^{2}+n|\mathrm{c}-\mathrm{x}|^{2}
$$等式右边第一部分是确定的数,第二部分最小值为0,在$x=c$处取得。
### 3、Lloyd's Algorithm
k-means聚类一个常用的算法是Lloyd's Algorithm。
**Lloyd's Algorithm:**
1. 初始化k个中心(随机选择?);
2. 将每个点与最靠近它的中心聚类;
3. 找到每个聚类的质心作为新中心替换旧中心;
4. 重复Step 2和Step 3直到聚类中心收敛(根据一些准则,例如k-means得分不再提高)
Lloyd算法不一定能找到全局最优解,但会找到局部最优解。算法中一个重要的步骤是初始化。下面的例子说明了初始中心会显著影响聚类结果。
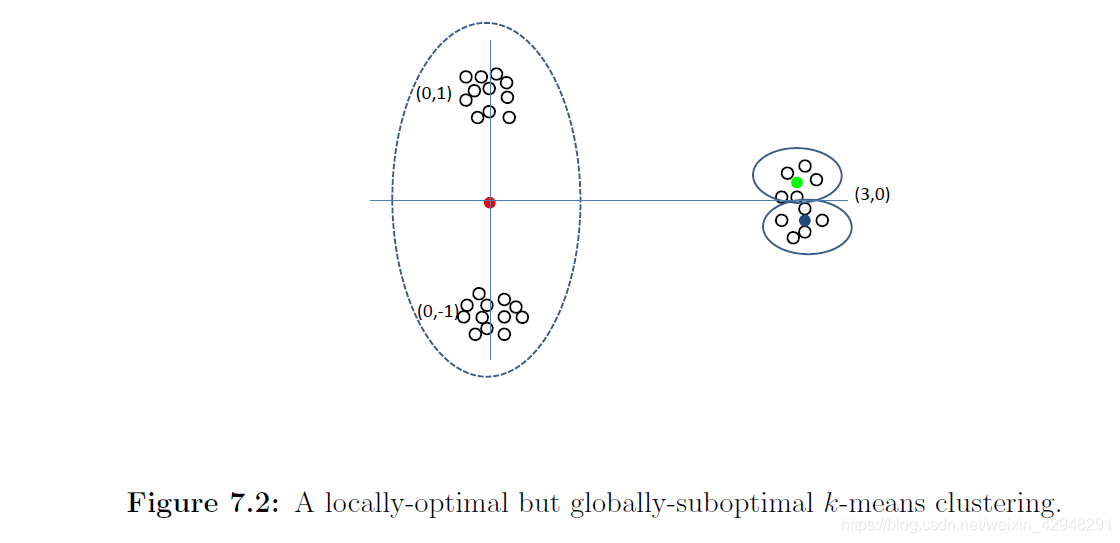
上图中有三个密集簇,分别以$(0,1),(0,-1)$和$(3,0)$为中心。但如果我们以一个中心$(0,1)$和两个接近$(3,0)$的中心初始化,那么$(0,1)$处的中心会移到$(0,0)$,而$(3,0)$处的两个中心会呆在那里,将这一簇分成两部分。

上图中有三个密集簇,分别以$(0,1),(0,-1)$和$(3,0)$为中心。但如果我们以一个中心$(0,1)$和两个接近$(3,0)$的中心初始化,那么$(0,1)$处的中心会移到$(0,0)$,而$(3,0)$处的两个中心会呆在那里,将这一簇分成两部分。
因此,对于初始中心的选择要遵循一定的策略。最常用的策略为“最远遍历”。首先选择一个数据点作为初始中心$c_1$,然后选择距离$c_1$最远的数据点作为$c_2$,然后选择距离$\{c_1,c_2\}$最远的数据点作为$c_3$,等等。直到选足了k个点,将它们用作初始中心。注意到,这样可以在图7.2中得到正确的聚类。
“最远便利”会被少数异常值欺骗。k-means++对此进行改进,基于它们与已挑选中心的距离来加权数据点,具体而言,与距离平方成比例。然后根据这些权重概率地选择下一个中心。另一种方法是为k-means问题运行一些其他近似算法,然后使用其输出作为Lloyd算法的起点。
### 4、Ward's Algorithm
从它自己的簇中的每个数据点开始,然后重复的合并成对的簇,直到只剩下k个簇。具体来说,Ward算法合并了最小化k-means成本增量的两个簇,即合并 $\left(C, C^{\prime}\right)$ minimizing
$$
\operatorname{cost}\left(C \cup C^{\prime}\right)-\operatorname{cost}(C)-\operatorname{cost}\left(C^{\prime}\right)
$$
### 4、一维中的k-Means聚类
假设已经得到了$a_{1}, \dots, a_{i}$的所有最优k'-means聚类($\forall k'\le k$), 要计算$a_{1}, \dots, a_{i+1}$的最优k'-means聚类,即寻找$j$,最小化
$$dist(a_1,\cdots,a_{j-1})+dist(a_j,\cdots,a_{i+1})$$
前者聚成$k'-1$类,后者聚成1类。
从它自己的簇中的每个数据点开始,然后重复的合并成对的簇,直到只剩下k个簇。具体来说,Ward算法合并了最小化k-means成本增量的两个簇,即合并 $\left(C, C^{\prime}\right)$ minimizing
$$
\operatorname{cost}\left(C \cup C^{\prime}\right)-\operatorname{cost}(C)-\operatorname{cost}\left(C^{\prime}\right)
$$
### 4、一维中的k-Means聚类
假设已经得到了$a_{1}, \dots, a_{i}$的所有最优k'-means聚类($\forall k'\le k$), 要计算$a_{1}, \dots, a_{i+1}$的最优k'-means聚类,即寻找$j$,最小化
$$dist(a_1,\cdots,a_{j-1})+dist(a_j,\cdots,a_{i+1})$$
前者聚成$k'-1$类,后者聚成1类。
对于给定的$i$,我们需要计算$k'=1,\cdots,k$,每次计算$a_{1}, \dots, a_{i}$的k'-means聚类时,需要运行$i$个$j$($i\le n$)。因此运行时间为$O(kn)$。而一共有$n$个$i$,因此总的运行时间为$O(kn^2$)。
## 三、k-Center Clustering
将任意点到聚类中心的最大距离称为聚类的半径。存在半径为r的k聚类当且仅当存在k个半径为r的球体将所有的点覆盖。下面,我们给出一个简单的算法来寻找k个球覆盖所有点。
**The Farthest Traversal k-clustering Algorithm**
将任意点到聚类中心的最大距离称为聚类的半径。存在半径为r的k聚类当且仅当存在k个半径为r的球体将所有的点覆盖。下面,我们给出一个简单的算法来寻找k个球覆盖所有点。
**The Farthest Traversal k-clustering Algorithm**
1. 任意选择一个点作为第一个聚类中心;
2. 对$t=2,3,\cdots,k$,选择距离当前聚类中心最远的点,作为第$t$个聚类中心。
2. 对$t=2,3,\cdots,k$,选择距离当前聚类中心最远的点,作为第$t$个聚类中心。
该算法相当于初始化Lloyd算法的最远遍历策略。下面的引理表明该算法仅需要使用最多为最佳k-center解的两倍的半径。
**Theorem 7.3** 如果存在半径为$\frac{r}{2}$的$k$聚类,那么上面的算法找到的$k$聚类的半径至多为$r$。
**证明**:若不然,即存在数据点$x$,它距离所有中心$>r$ $\Rightarrow$ 每次产生的新中心距离当前中心$>r$ (否则它就不是距离当前中心最远的点,因为$x$距离当前中心$>r$ )。从而,$k$个中心加上一个数据点$x$,共有$k+1$个数据点,它们的距离成对的比$r$更大。但在半径为$\frac{r}{2}$的$k$聚类中,没有两个这样的点可以属于同一簇,矛盾。
## 四、Spectral Clustering(谱聚类)
Spectral Clustering 其实就是通过 Laplacian Eigenmap 的降维方式降维之后再做 K-means 的一个过程。
谱聚类遵循以下步骤:
**Theorem 7.3** 如果存在半径为$\frac{r}{2}$的$k$聚类,那么上面的算法找到的$k$聚类的半径至多为$r$。
**证明**:若不然,即存在数据点$x$,它距离所有中心$>r$ $\Rightarrow$ 每次产生的新中心距离当前中心$>r$ (否则它就不是距离当前中心最远的点,因为$x$距离当前中心$>r$ )。从而,$k$个中心加上一个数据点$x$,共有$k+1$个数据点,它们的距离成对的比$r$更大。但在半径为$\frac{r}{2}$的$k$聚类中,没有两个这样的点可以属于同一簇,矛盾。
## 四、Spectral Clustering(谱聚类)
Spectral Clustering 其实就是通过 Laplacian Eigenmap 的降维方式降维之后再做 K-means 的一个过程。
谱聚类遵循以下步骤:
- 寻找由A的前k个右奇异向量生成的空间V
- 将数据点投影到V上
- 对投影点聚类
### 1、为什么要投影?
投影会使数据点更接近其聚类中心。
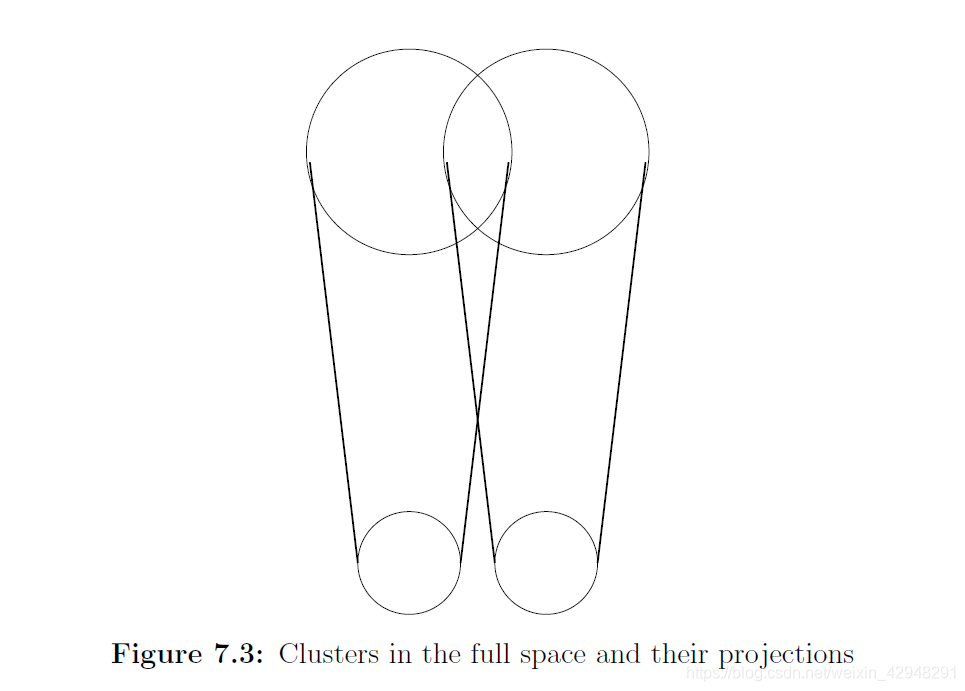
令数据矩阵$A$的第$i$行表示第$i$个数据点,C的第$i$行表示第$i$个数据点属于的中心点。(对于$k$聚类问题有且仅有$k$个不同行)那么,数据点到其聚类中心的距离平方和为
$$
\sum_{i=1}^{n}\left|\mathbf{a}_{\mathbf{i}}-\mathbf{c _ { i }}\right|^{2}=\|A-C\|_{F}^{2}
$$
通过聚类能够将到聚类中心的距离平方和由$\|A-C\|_{F}^{2}$减小到投影中的8$k\|A-C\|_{2}^{2}$.。
**Theorem 7.4** 对任意秩小于等于k的矩阵$C$,有
$$
\left\|A_{k}-C\right\|_{F}^{2} \leq 8 k\|A-C\|_{2}^{2}
$$
**证明**:$$rank(A_k-C)\le rank(A_k) + rank(C)\le k+k=2k$$
由于$\|A\|_{2}^{2} \leq\|A\|_{F}^{2} \leq k\|A\|_{2}^{2}$,所以
$$
\left\|A_{k}-C\right\|_{F}^{2} \leq 2 k\left\|A_{k}-C\right\|_{2}^{2}
$$
又
$$
\left\|A_{k}-C\right\|_{2} \leq\left\|A_{k}-A\right\|_{2}+\|A-C\|_{2} \leq 2\|A-C\|_{2}
$$
得证。
### 2、算法
定义$\sigma(C)=\|A-C\|_{2} / \sqrt{n}$。
**Spectral Clustering - The Algorithm**
- 寻找A的前k个奇异值向量,然后将A的列投影到由这向量生成的空间上,得到$A_k$;
- 从$A_k$中选择一行进行聚类,使得$A_k$的所有行与该行的距离都小于$6k \sigma(C) / \varepsilon$;
- 重复Step 2 $k$次。
- 将数据点投影到V上
- 对投影点聚类
### 1、为什么要投影?
投影会使数据点更接近其聚类中心。

令数据矩阵$A$的第$i$行表示第$i$个数据点,C的第$i$行表示第$i$个数据点属于的中心点。(对于$k$聚类问题有且仅有$k$个不同行)那么,数据点到其聚类中心的距离平方和为
$$
\sum_{i=1}^{n}\left|\mathbf{a}_{\mathbf{i}}-\mathbf{c _ { i }}\right|^{2}=\|A-C\|_{F}^{2}
$$
通过聚类能够将到聚类中心的距离平方和由$\|A-C\|_{F}^{2}$减小到投影中的8$k\|A-C\|_{2}^{2}$.。
**Theorem 7.4** 对任意秩小于等于k的矩阵$C$,有
$$
\left\|A_{k}-C\right\|_{F}^{2} \leq 8 k\|A-C\|_{2}^{2}
$$
**证明**:$$rank(A_k-C)\le rank(A_k) + rank(C)\le k+k=2k$$
由于$\|A\|_{2}^{2} \leq\|A\|_{F}^{2} \leq k\|A\|_{2}^{2}$,所以
$$
\left\|A_{k}-C\right\|_{F}^{2} \leq 2 k\left\|A_{k}-C\right\|_{2}^{2}
$$
又
$$
\left\|A_{k}-C\right\|_{2} \leq\left\|A_{k}-A\right\|_{2}+\|A-C\|_{2} \leq 2\|A-C\|_{2}
$$
得证。
### 2、算法
定义$\sigma(C)=\|A-C\|_{2} / \sqrt{n}$。
**Spectral Clustering - The Algorithm**
- 寻找A的前k个奇异值向量,然后将A的列投影到由这向量生成的空间上,得到$A_k$;
- 从$A_k$中选择一行进行聚类,使得$A_k$的所有行与该行的距离都小于$6k \sigma(C) / \varepsilon$;
- 重复Step 2 $k$次。
**Theorem 7.5** 如果在$k$聚类$C$中,每对中心间隔至少15$k \sigma(C) / \varepsilon$,并且每一类中至少有$\varepsilon n$个点,则以至少$1-\varepsilon$的概率,谱聚类找到的聚类$C'$与$C$至多有$\varepsilon^{2} n$个点不同。
**证明**:首先证明对大多数的数据点,数据点的投影与其聚类中心的距离在$3k \sigma(C) / \varepsilon$以内。令
$$
M=\left\{i :\left|\mathbf{v}_{\mathrm{i}}-\mathbf{c}_{\mathrm{i}}\right| \geq 3 k \sigma(C) / \varepsilon\right\}
$$
其中$\mathbf{v}_i$表示$A_k$的第$i$行。下面证明$|M|$是小的。
由于$\left\|A_{k}-C\right\|_{F}^{2}=\sum_{i}\left|\mathrm{v}_{\mathrm{i}}-\mathrm{c}_{\mathrm{i}}\right|^{2} \geq \sum_{i \in M}\left|\mathrm{v}_{\mathrm{i}}-\mathrm{c}_{\mathrm{i}}\right|^{2} \geq|M| \frac{9 k^{2} \sigma^{2}(C)}{\varepsilon^{2}}$,所以,由定理7.4,有
$$
|M| \frac{9 k^{2} \sigma^{2}(C)}{\varepsilon^{2}} \leq\left\|A_{k}-C\right\|_{F}^{2} \leq 8 k n \sigma^{2}(C) \quad \Longrightarrow \quad|M| \leq \frac{8 \varepsilon^{2} n}{9 k}
$$
如果$i \notin M$,称数据点$i$是好的。对于属于同一簇的两个好点$i$和$j$,由于它们的投影与中心距离在$3k \sigma(C) / \varepsilon$以内,所以两个点的投影距离在$6k \sigma(C) / \varepsilon$以内。另一方面,对于属于不同簇的两个好点$i$和$k$,由于两个簇的中心间隔至少15$k \sigma(C) / \varepsilon$,所以两个点的投影距离一定比$15 k \sigma(C) / \varepsilon-6 k \sigma(C) / \varepsilon=9 k \sigma(C) / \varepsilon$大。因此,如果我们在Step 2中选择了一个好点(如点$i$),那么我们算法放置在它的簇中的好点就确为与$i$在同一簇中的好点。因此,如果在Step 2的第k次执行中,我们选择了一个好点,那么所有好点都被正确聚类。又由于$|M| \leq \varepsilon^{2} n$,定理即成立。
为了完成证明,,我们还需说明Step 2中选择坏点的可能性很小。有上面证明,可知每一类中好点的个数至少$(\varepsilon-\varepsilon^2)n$。因此,从每一类中挑出好点的概率至少为$(\varepsilon-\varepsilon^2)n/(\varepsilon n)=1-\varepsilon$。
### 3、由$\Omega(1)$标准差分离的均值
对于实线上的概率分布,“由$6$标准差分离的均值”足够区分不同的分布。如果$k \in O(1)$并且$6$被一些常数代替,则谱聚类能够使我们在更高维度上做同样的事。首先定义标准偏差为数据点到聚类中心的平方均值在所有单位方向$\mathrm{v}$上的最大值,即
$$
\sigma(C)^{2}=\frac{1}{n} \max\limits_{|\mathbf{v}|=1} \sum_{i=1}^{n}\left[\left(\mathbf{a}_{\mathbf{i}}-\mathbf{c}_{\mathbf{i}}\right) \cdot \mathbf{v}\right]^{2}=\frac{1}{n} \max\limits_{|\mathbf{v}|=1}|(A-C) \mathbf{v}|^{2}=\frac{1}{n}\|A-C\|_{2}^{2}
$$
这也与我们之前对$\sigma(C)$的定义相同。
现在,很容易看出Theorem 7.5可以重新表述(假设$k \in O(1)$)为
**证明**:首先证明对大多数的数据点,数据点的投影与其聚类中心的距离在$3k \sigma(C) / \varepsilon$以内。令
$$
M=\left\{i :\left|\mathbf{v}_{\mathrm{i}}-\mathbf{c}_{\mathrm{i}}\right| \geq 3 k \sigma(C) / \varepsilon\right\}
$$
其中$\mathbf{v}_i$表示$A_k$的第$i$行。下面证明$|M|$是小的。
由于$\left\|A_{k}-C\right\|_{F}^{2}=\sum_{i}\left|\mathrm{v}_{\mathrm{i}}-\mathrm{c}_{\mathrm{i}}\right|^{2} \geq \sum_{i \in M}\left|\mathrm{v}_{\mathrm{i}}-\mathrm{c}_{\mathrm{i}}\right|^{2} \geq|M| \frac{9 k^{2} \sigma^{2}(C)}{\varepsilon^{2}}$,所以,由定理7.4,有
$$
|M| \frac{9 k^{2} \sigma^{2}(C)}{\varepsilon^{2}} \leq\left\|A_{k}-C\right\|_{F}^{2} \leq 8 k n \sigma^{2}(C) \quad \Longrightarrow \quad|M| \leq \frac{8 \varepsilon^{2} n}{9 k}
$$
如果$i \notin M$,称数据点$i$是好的。对于属于同一簇的两个好点$i$和$j$,由于它们的投影与中心距离在$3k \sigma(C) / \varepsilon$以内,所以两个点的投影距离在$6k \sigma(C) / \varepsilon$以内。另一方面,对于属于不同簇的两个好点$i$和$k$,由于两个簇的中心间隔至少15$k \sigma(C) / \varepsilon$,所以两个点的投影距离一定比$15 k \sigma(C) / \varepsilon-6 k \sigma(C) / \varepsilon=9 k \sigma(C) / \varepsilon$大。因此,如果我们在Step 2中选择了一个好点(如点$i$),那么我们算法放置在它的簇中的好点就确为与$i$在同一簇中的好点。因此,如果在Step 2的第k次执行中,我们选择了一个好点,那么所有好点都被正确聚类。又由于$|M| \leq \varepsilon^{2} n$,定理即成立。
为了完成证明,,我们还需说明Step 2中选择坏点的可能性很小。有上面证明,可知每一类中好点的个数至少$(\varepsilon-\varepsilon^2)n$。因此,从每一类中挑出好点的概率至少为$(\varepsilon-\varepsilon^2)n/(\varepsilon n)=1-\varepsilon$。
### 3、由$\Omega(1)$标准差分离的均值
对于实线上的概率分布,“由$6$标准差分离的均值”足够区分不同的分布。如果$k \in O(1)$并且$6$被一些常数代替,则谱聚类能够使我们在更高维度上做同样的事。首先定义标准偏差为数据点到聚类中心的平方均值在所有单位方向$\mathrm{v}$上的最大值,即
$$
\sigma(C)^{2}=\frac{1}{n} \max\limits_{|\mathbf{v}|=1} \sum_{i=1}^{n}\left[\left(\mathbf{a}_{\mathbf{i}}-\mathbf{c}_{\mathbf{i}}\right) \cdot \mathbf{v}\right]^{2}=\frac{1}{n} \max\limits_{|\mathbf{v}|=1}|(A-C) \mathbf{v}|^{2}=\frac{1}{n}\|A-C\|_{2}^{2}
$$
这也与我们之前对$\sigma(C)$的定义相同。
现在,很容易看出Theorem 7.5可以重新表述(假设$k \in O(1)$)为
- 如果$C$中的聚类中心可以由$\Omega(\sigma(C))$分离,那么谱聚类算法找到的聚类$C'$与$C$只有很小一部分数据点不同。
可以看出,对于许多随机模型,“均值由$\Omega(1)$标准差分离”条件成立。在这里用两个例子说明。
首先,假设我们有$k \in O(1)$个球面高斯的混合,其标准差均为1。数据由这个混合产生。如果高斯的均值是$\Omega(1)$分离的,那么条件“均值由$\Omega(1)$标准差分离”是满足的,因此当我们投影到SVD子空间并聚类,我们将得到(接近)正确的聚类。
我们再讨论第二个例子。随机块模型是关于社区的模型。假设再$n$个人中有$k$个社区$C_{1}, C_{2}, \ldots, C_{k}$。假设两个人在同一社区认识对方的概率为$p$,在不同社区认识对方的概率为$q$,其中,$q<p$。假设事件人$i$认识人$j$是互相独立的。具体地,我们给出$n\times n$数据矩阵,其中$a_{ij}=1$当且仅当$i$和$j$彼此认识。可以将A视为图的邻接矩阵。在实际中,图形相当稀疏,即$p$和$q$很小,即$O(1 / n)$ or $O(\ln n / n)$。
考虑简单情形:两个社区各有$n/2$个人,且$p=\frac{\alpha}{n} \quad q=\frac{\beta}{n} \quad$ ,其中$\alpha, \beta \in O(\ln n)$。令$\mathbf{u}$和$\mathbf{v}$分别为社区一和二的数据点的质心,所以$u_{i} \approx p$ for $i \in C_{1}$和 $u_{j} \approx q$ for $j \in C_{2}$ 并且$v_{i} \approx q$ for $i \in C_{1}$ 和$v_{j} \approx p$ for $j \in C_{2}$。我们有
$$
|\mathbf{u}-\mathbf{v}|^{2}=\sum_{j=1}^{n}\left(u_{j}-v_{j}\right)^{2} \approx \frac{(\alpha-\beta)^{2}}{n^{2}} n=\frac{(\alpha-\beta)^{2}}{n}
$$
$$Inter-centroid distance\approx \frac{\alpha-\beta}{\sqrt{n}}$$
我们要求$\|A-C\|_{2}$的上界。这是非平凡的,因为我们必须对所有单位向量$\mathbf{v}$证明一个统一的上界。随机矩阵(RMT)理论已经为我们做了这个。RMT告诉我们$$
\|A-C\|_{2} \leq O^{*}(\sqrt{n p})=O^{*}(\sqrt{\alpha})
$$
因此,只要$\alpha-\beta \in \Omega^{*}(\sqrt{\alpha})$,我们有$\Omega(1)$标准差分离的均值,从而谱聚类工作。
### 4、拉普拉斯算子
谱聚类的一个重要特例是当$k=2$时。如果我们一个算法将数据分成两部分,这可以递归的应用。一种使用该谱算法的情形是应用在图的拉普拉斯矩阵L上,其被定义为
$$L=D-A$$
其中$A$是邻接矩阵,$D$是自由度的对角矩阵。我们令$A$为负号。
对任意向量$x$,我们有
$$
\mathbf{x}^{T} L \mathbf{x}=\sum_{i} d_{i i} x_{i}^{2}-\sum_{(i, j) \in E} x_{i} x_{j}=\frac{1}{2} \sum_{(i, j) \in E}\left(x_{i}-x_{j}\right)^{2}
$$
由于$L$的所有行和为0,因此其最小特征值为0,对应的特征向量为$\mathbf{1}$。所有数据点对此向量的投影点仅仅是原点,因此不能提供任何信息。如果我们采用第二低的奇异向量并进行投影,我们得到非常简单的将$n$个实数进行聚类的问题。
考虑简单情形:两个社区各有$n/2$个人,且$p=\frac{\alpha}{n} \quad q=\frac{\beta}{n} \quad$ ,其中$\alpha, \beta \in O(\ln n)$。令$\mathbf{u}$和$\mathbf{v}$分别为社区一和二的数据点的质心,所以$u_{i} \approx p$ for $i \in C_{1}$和 $u_{j} \approx q$ for $j \in C_{2}$ 并且$v_{i} \approx q$ for $i \in C_{1}$ 和$v_{j} \approx p$ for $j \in C_{2}$。我们有
$$
|\mathbf{u}-\mathbf{v}|^{2}=\sum_{j=1}^{n}\left(u_{j}-v_{j}\right)^{2} \approx \frac{(\alpha-\beta)^{2}}{n^{2}} n=\frac{(\alpha-\beta)^{2}}{n}
$$
$$Inter-centroid distance\approx \frac{\alpha-\beta}{\sqrt{n}}$$
我们要求$\|A-C\|_{2}$的上界。这是非平凡的,因为我们必须对所有单位向量$\mathbf{v}$证明一个统一的上界。随机矩阵(RMT)理论已经为我们做了这个。RMT告诉我们$$
\|A-C\|_{2} \leq O^{*}(\sqrt{n p})=O^{*}(\sqrt{\alpha})
$$
因此,只要$\alpha-\beta \in \Omega^{*}(\sqrt{\alpha})$,我们有$\Omega(1)$标准差分离的均值,从而谱聚类工作。
### 4、拉普拉斯算子
谱聚类的一个重要特例是当$k=2$时。如果我们一个算法将数据分成两部分,这可以递归的应用。一种使用该谱算法的情形是应用在图的拉普拉斯矩阵L上,其被定义为
$$L=D-A$$
其中$A$是邻接矩阵,$D$是自由度的对角矩阵。我们令$A$为负号。
对任意向量$x$,我们有
$$
\mathbf{x}^{T} L \mathbf{x}=\sum_{i} d_{i i} x_{i}^{2}-\sum_{(i, j) \in E} x_{i} x_{j}=\frac{1}{2} \sum_{(i, j) \in E}\left(x_{i}-x_{j}\right)^{2}
$$
由于$L$的所有行和为0,因此其最小特征值为0,对应的特征向量为$\mathbf{1}$。所有数据点对此向量的投影点仅仅是原点,因此不能提供任何信息。如果我们采用第二低的奇异向量并进行投影,我们得到非常简单的将$n$个实数进行聚类的问题。