opencv图像处理学习（五十二）——拟合（最小二乘法）

怀着沉痛的心情，拖着疲惫的身心，为了拟合好圆，我实在不得不上最小二乘法了(我上班写的代码不要想了，不可能发在blog里的)，现在进入正题。

（1）基本原理

名称
自变量：x	$x_{1}$	$x_{2}$	$x_{3}$	……	$x_{n-1}$	$x_{n}$
函数（因变量）：y	$f(x_{1})$	$f(x_{2})$	$f(x_{3})$	……	$f(x_{n-1})$	$f(x_{n})$

求以下拟合函数： $\phi (x) = a_{0}\phi _{0}(x)+a_{1}\phi _{1}(x)+\cdots +a_{n}\phi _{n}(x)=\sum_{i=1}^{m}a_{j}\phi _{j}(x)$ ，

使得： $\sum_{i=1}^{m}[\phi (x_{i})-y_{i}] ^{2}=\sum_{i=1}^{m}[\sum_{j=0}^{n}a_{j}\phi _{j}(x_{i})-y_{i}]^{2}$

拟合条件：拟合曲线与各数据点在y方向的误差平方和最小.

拟合函数为一元函数时--函数图形为平面曲线--曲线拟合

解决曲线拟合，最先是确定拟合函数的形式。即适当选取

选幂函数{1,x,x2, ···,xn}, 则多项式拟合函数φ(x)可表示为：

$\phi (x) = a_{0}+a_{1}x+a_{2}x^{2}+\cdots +a_{n-1}x^{n-1}+a_{n}x^{n}=\begin{bmatrix} a_{0}\\ a_{1}\\ \cdots \ \\ a_{n-1} \\ a_{n} \end{bmatrix} \begin{bmatrix} 1 & x &\cdots &x^{n-1} &x^{n} \end{bmatrix}$

PS:常见的曲线拟合方法:

1.使偏差绝对值之和最小

2.使偏差绝对值最大的最小

3.使偏差平方和最小

按偏差平方和最小的原则选取拟合曲线，并且采取二项式方程为拟合曲线的方法,称为最小二乘法。

a0、a1、a2......an是幂系数，也是拟合所求的未知量。
实际中拟合函数有指数函数、三角函数等，根据数据的分布特点来选取合适的拟合函数。
将第 i 个样本点的x坐标带入φ(x)，得到：

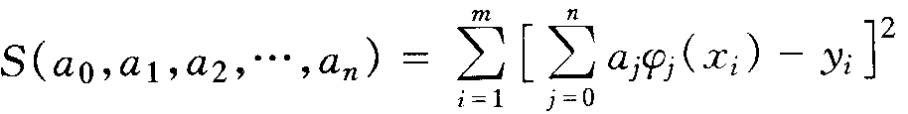
实际中拟合函数有指数函数、三角函数等，根据数据的分布特点来选取合适的拟合函数。

这个就是二次方程，我们期望S最小。此时，方程中的x、y已知，想求的是a0 a1 a2 ...... an。

S最小的必要条件是：

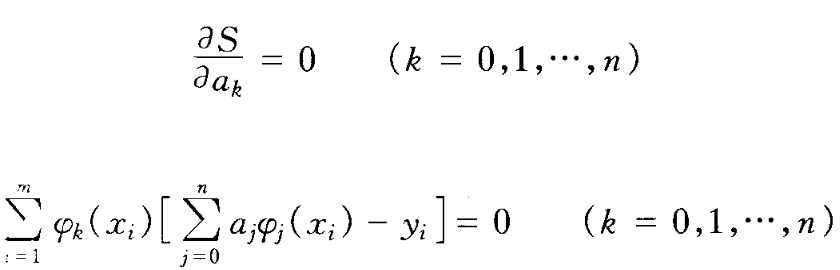
整理得到如下正规方程组：

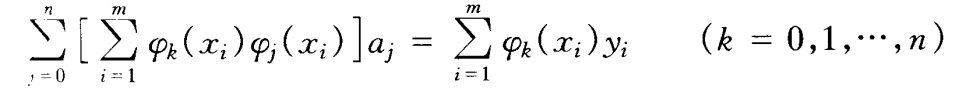
解此方程组得系数a0 a1 a2 ...... an，, 得出拟合函数φ(x)

最小二乘法：以残差平方和最小问题的解来确定拟合函数

二、超定方程组得最小二乘解

将

写成向量内积形式：

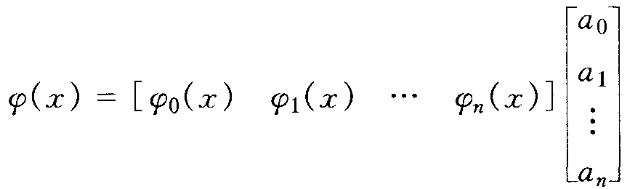
a0 a1 a2 ...... an为待定系数，满足：

此m个等式如下建立方程组：

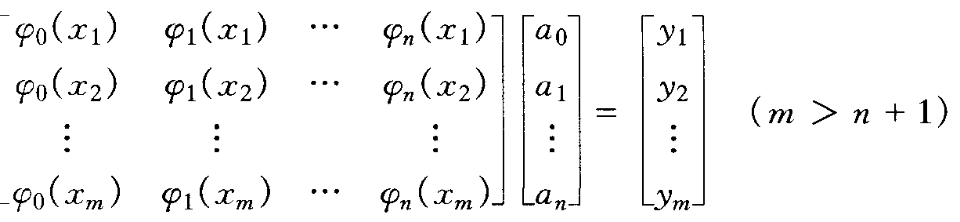
方程数(m)多于未知数个数(n+1)，此类方程组称为超定方程组。下列正规方程组中k个方程中aj的系数

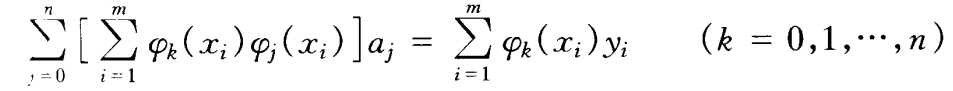
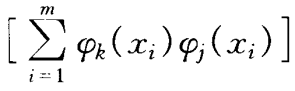
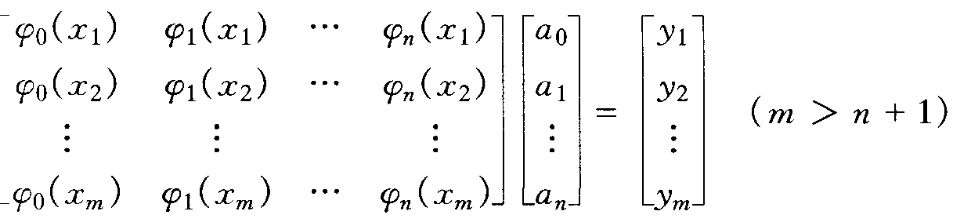
经推导，得到最小二次方，幂函数拟合公式如下：

ΦT* Φ*a= ΦT*y

其中Φ是样本点坐标x的超定矩阵，将所有x带入该向量[1 x x^2 ... ... x^n]中，就得到超定矩阵Φ。ΦT表示Φ的转置

把这些等式表示成矩阵的形式，就可以得到下面的矩阵：

即X*A=Y。

我们只要解出这个线性方程，即可求得拟合曲线多项式的系数矩阵。而在opencv中，有一个专门用于求解线性方程的函数，即cv::solve()，具体调用形式如下：

int cv::solve( cv::InputArray X, // 左边矩阵X, nxn cv::InputArray Y, // 右边矩阵Y,nx1 cv::OutputArray A, // 结果，系数矩阵A,nx1 int method = cv::DECOMP_LU // 估算方法);

我们只需要按照上述原理，构造出矩阵X和Y，即可调用该函数，计算出多项式的系数矩阵A

opencv图像处理学习（五十二）——拟合（最小二乘法）

二、超定方程组得最小二乘解

猜你喜欢