动态规划与记忆化搜索

1. 01背包

　　递推式：

　　注意这里的物品在数组中是从 0 开始的。

int dp[MAX_N + 1][MAX_W + 1];
void solve() {
    for (int i = 0; i < n; i++) {
        for (int j = 0; j <= W; j++) {
            if (j < w[i])
                dp[i + 1][j] = dp[i][j];
            else
                dp[i + 1][j] = max(dp[i][j], dp[i][j - w[i]] + v[i]);
        }
    } 
    printf("%d\n", dp[n][W]);
}

2. 最长公共子序列问题 (LCS, Longest Common Subsequence)

　　这里我们定义 dp[i][j] = s1 ...... si 和 t1.....ti 为对应的 LCS 的长度

　　那么， s1 ..... s _i+1 和 t1 ..... t _i+1对应的公共子列可能是下面三种情况：

　　（1）当 s _{i+1 = t _i+1 时， LCS 就是在末尾追加上s _{i+1 ；}}

　　（2） LCS 为 S1 ..... Si 和 t1 ..... t _i+1的公共子列

　　（3）LCS 为 s1 ..... s _{i+1 和 t1.....ti}的公共子列

由此就可以得到递推式：

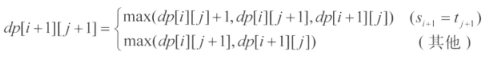
int n, m;
char s[MAX_N], t[MAX_M];

int dp[MAX_N + 1][MAX_W + 1];

void solve() {
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (s[i] == t[j])
                dp[i + 1][j + 1] = dp[i][j] + 1;
            else
                dp[i + 1][j + 1] = max(dp[i][j + 1] , dp[i + 1][j]);
        }
    } 
    printf("%d\n", dp[n][m]);
}

3.完全背包问题

　　这次相比于 01 背包，同一种的物品可以取任意多件了，那么我们再试着写递推式：

　　还是令 dp[i + 1][j] = 从前 i 种物品挑选总重量不超过 j 时总价值的最大值。那么递推关系为

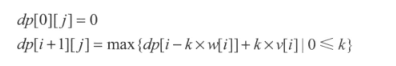
int dp[MAX_N + 1][MAX_W + 1];

void solve() {
    for (int i = 0; i < n; i++)
        for (int j = 0; j <= W; j++)
            for (int k = 0; k * w[i] <= j; k++) 
                dp[i + 1][j] = max(dp[i + 1][j], dp[i][j - k * w[i]] + k * v[i]);
    printf("%d\n", dp[n][W]);
}

　　这里有三重循环，时间复杂度有0 （nW²），这样并不理想。当我们仔细分析整个过程会发现有一些重复计算。下面我们打表看一下 dp 数组的结果分析一下：

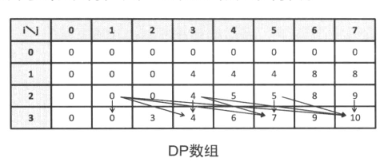
　　这里我们来以 dp[3][5] 和 dp[3][7] 为例来分析一下：

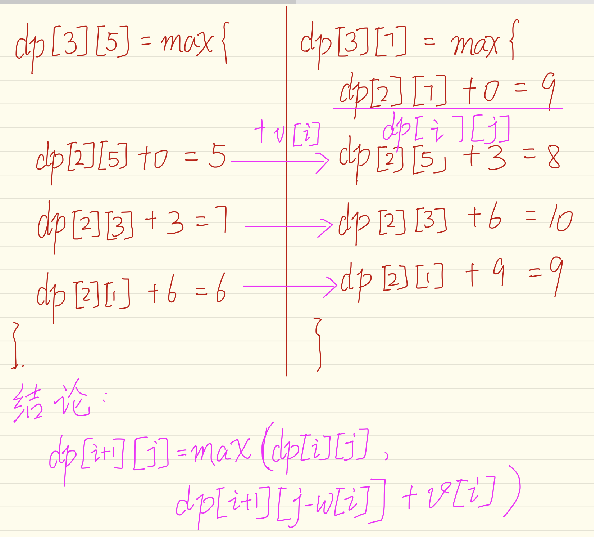
　　可以看出 dp[i+1][j] 递推过程中 k ≥ 1 的部分计算已经在 dp[i + 1][ j - w[i] ] 中计算完成了。

　　这样就不需要关于 k 的循环了，优化后的时间复杂度为 0（nW）。

void solve() {
    for (int i = 0; i < n; i++)
        for (int j = 0; j <= W; j++) {
            if (j < w[i])
                dp[i + 1][j] = dp[i][j];
            else
                dp[i + 1][j] = max(dp[i][j], dp[i + 1][j - w[i]] + v[i]);
        }
    printf("%d\n", dp[n][W]);
}

　　此外，前面的 01背包和这里的完全背包问题，可以通过不断重复利用一个数组实现，来降低空间复杂度。

　　01 背包问题情况

int dp[MAX_N + 1];

void solve() {
    for (int i = 0; i < n; i++)
        for (int j = W; j >= w[i]; j--) {
            dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
    printf("%d\n", dp[n][W]);
}

　　完全背包问题情况

int dp[MAX_N + 1];

void solve() {
    for (int i = 0; i < n; i++)
        for (int j = w[i]; j <= W; j++) {
            dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
    printf("%d\n", dp[n][W]);
}

　　像这样写的话，两者的差异就变成了只有循环的方向了。重复利用数组可以节省内存空间，但使用不好可能会留下 bug ，所以使用要小心。不过出于节约内存的考虑，有时候必须要重复利用数组，也存在通过重复利用数组能够进一步降低复杂度的问题。

动态规划与记忆化搜索

猜你喜欢