编程之法-面试和算法心得 - 红黑树

《编程之法-面试和算法心得》

本章导读

1. 红黑树

1.1 二叉查找树

二叉查找树（Binary Search Tree），也称有序二叉树（ordered binary tree）,排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

• 若任意结点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若任意结点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 任意结点的左、右子树也分别为二叉查找树。
• 没有键值相等的结点（no duplicate nodes）。

一般操作的执行时间为O（logn）.
但二叉树若退化成了一棵具有n个结点的线性链后，则此些操作最坏情况运行时间为O（n）

1.2 红黑树

红黑树的查找、插入、删除的时间复杂度最坏为O(log n)
红黑树的5条性质：

1）每个结点要么是红的，要么是黑的。
2）根结点是黑的。
3）每个叶结点（叶结点即指树尾端NIL指针或NULL结点）是黑的。
4）如果一个结点是红的，那么它的俩个儿子都是黑的。 (不存在连续2个红色节点)
5）对于任一结点而言，其到叶结点树尾端NIL指针的每一条路径都包含相同数目的黑结点。


上文中我们所说的 “叶结点” 或"NULL结点"，它不包含数据而只充当树在此结束的指示

1.3 树的旋转知识

树的旋转，分为左旋和右旋

1. 左旋
   
   左旋以pivot到y之间的链为“支轴”进行，它使y成为该孩子树新的根，而y的左孩子b则成为pivot的右孩子。

左旋代码（以x代替上述的pivot）：

LEFT-ROTATE(T, x)  
  y ← right[x] 			  ▹ Set y.  
  right[x] ← left[y]      ▹ Turn y's left subtree into x's right subtree.  
  p[left[y]] ← x  
  p[y] ← p[x]             ▹ Link x's parent to y.  
  if p[x] = nil[T]  
     then root[T] ← y  
     else if x = left[p[x]]  
             then left[p[x]] ← y  
             else right[p[x]] ← y  
  left[y] ← x             ▹ Put x on y's left.  
  p[x] ← y

• (将y的左子树放到x的右子树，将y的左子树的父节点设为x)
• ( 将x的父节点作为y的父节点，
  • 如果x无父节点，则y为root
  • 如果x是父节点的左子树，则将父节点的左子树设为y
  • 如果x是父节点的右子树，则将父节点的右子树设为y)
• (then, 将x设为y的左子树，将y作为x的右子树 )
  综上，每次变换，包含2个步骤，1. 修改子节点，2.修改父节点。
  上述步骤共有3次交换，1是y的左子树；2.是y修改为x父节点的儿子；3是x修改为y的左子树。

2. 右旋
   右旋与左旋差不多，再此不做详细介绍。
   

1.4 红黑树的插入

二叉查找树的插入

如果要在二叉查找树中插入一个结点，首先要查找到结点插入的位置，然后进行插入，假设插入的结点为z的话，插入的伪代码如下：
思想：如果插入结点z小于当前遍历到的结点，则到当前结点的左子树中继续查找，如果z大于当前结点，则到当前结点的右子树中继续查找

TREE-INSERT(T, z)
 1  y ← NIL
 2  x ← root[T]
 3  while x ≠ NIL
 4      do y ←  x
 5         if key[z] < key[x]
 6            then x ← left[x]
 7            else x ← right[x]
 8  p[z] ← y
 9  if y = NIL
10     then root[T] ← z              ⊹ Tree T was empty
11     else if key[z] < key[y]
12             then left[y] ← z
13             else right[y] ← z

红黑树的插入和插入修复

假设插入的结点为z，红黑树的插入伪代码具体如下所示：
思想：将z按二叉查找树进行插入，将z节点着色为红色，最后调用RB-INSERT-FIXUP对节点进行重新着色并旋转。

RB-INSERT(T, z)  
  TREE-INSERT(T, z)
  left[z] ← nil[T]  
  right[z] ← nil[T]  
  color[z] ← RED  
  RB-INSERT-FIXUP(T, z)

现在分情况进行讨论：

• 如果插入的是根节点，违反性质2，将节点涂为黑色即可
• 如果当前节点的父节点是黑色，没有违反，什么也不做
• 如果当前节点的父节点是红色
  • 插入修复情况1：祖父节点的另一个子节点(叔叔节点)是红色
  • 插入修复情况2：叔叔节点是黑色，当前节点是父节点的右子
  • 插入修复情况3：叔叔节点是黑色，当前节点是父节点的左子

插入修复情况1：当前结点的父结点是红色且祖父结点的另一个子结点（叔叔结点）是红色

此时父结点的父结点一定存在，否则插入前就已不是红黑树。
与此同时，又分为父结点是祖父结点的左子还是右子，对于对称性，我们只要解开一个方向就可以了。

在此，我们只考虑父结点为祖父左子的情况。
同时，还可以分为当前结点是其父结点的左子还是右子，但是处理方式是一样的。我们将此归为同一类。

对策：将当前结点的父结点和叔叔结点涂黑，祖父结点涂红，把当前结点指向祖父结点，从新的当前结点重新开始算法。（case1）

变化前（当前节点为4）

变化后，

插入修复情况2：当前节点的父节点为红色，叔叔节点是黑色，当前节点是其父节点的右子

对策：当前节点的父节点作为新的当前节点，以新的当前节点为支点左旋。

变化前（当前节点为7）

变化后：

插入修复情况3：当前结点的父结点是红色,叔叔结点是黑色，当前结点是其父结点的左子

解法：父结点变为黑色，祖父结点变为红色，在祖父结点为支点右旋
最后，把根结点涂为黑色，整棵红黑树便重新恢复了平衡。

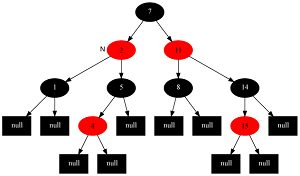
如下图所示（当前节点为2）：

变化后：

综上，代码如下

RB-INSERT-FIXUP（T,z）
 1 while color[p[z]] = RED  
 2     do if p[z] = left[p[p[z]]]  
 3           then y ← right[p[p[z]]]  
 4                if color[y] = RED  
 5                   then color[p[z]] ← BLACK                    ▹ Case 1  
 6                        color[y] ← BLACK                       ▹ Case 1  
 7                        color[p[p[z]]] ← RED                   ▹ Case 1  
 8                        z ← p[p[z]]                            ▹ Case 1  
 9                   else if z = right[p[z]]  
10                           then z ← p[z]                       ▹ Case 2  
11                                LEFT-ROTATE(T, z)              ▹ Case 2  
12                           color[p[z]] ← BLACK                 ▹ Case 3  
13                           color[p[p[z]]] ← RED                ▹ Case 3  
14                           RIGHT-ROTATE(T, p[p[z]])            ▹ Case 3  
15           else (same as then clause  
                         with "right" and "left" exchanged)  
16 color[root[T]] ← BLACK

1.5 红黑树的删除

二叉查找树的删除

待删除的结点按照儿子的个数可以分为三种：

1. 没有儿子，即为叶节点。直接把父节点对应的儿子指针设为NULL，删除儿子节点即可。
2. 只有一个儿子。父节点指向儿子的独生子，删除儿子节点。
3. 有两个儿子。选择左儿子中最大元素或者右儿子最小元素放到待删除节点的位置，然后调整子树。

二叉搜索树代码如下：

TREE-DELETE(T, z)
 1  if left[z] = NIL or right[z] = NIL
 2      then y ← z
 3      else y ← TREE-SUCCESSOR(z)
 4  if left[y] ≠ NIL
 5      then x ← left[y]
 6      else x ← right[y]
 7  if x ≠ NIL
 8      then p[x] ← p[y]
 9  if p[y] = NIL
10      then root[T] ← x
11      else if y = left[p[y]]
12              then left[p[y]] ← x
13              else right[p[y]] ← x
14  if y ≠ z
15      then key[z] ← key[y]
16           copy y's satellite data into z
17  return y

红黑树的删除和删除修复

RB-DELETE(T, z) 单纯删除结点的总操作：

 1 if left[z] = nil[T] or right[z] = nil[T]  
 2    then y ← z  
 3    else y ← TREE-SUCCESSOR(z)  
 4 if left[y] ≠ nil[T]  
 5    then x ← left[y]  
 6    else x ← right[y]  
 7 p[x] ← p[y]  
 8 if p[y] = nil[T]  
 9    then root[T] ← x  
10    else if y = left[p[y]]  
11            then left[p[y]] ← x  
12            else right[p[y]] ← x  
13 if y ≠ z  
14    then key[z] ← key[y]  
15         copy y's satellite data into z  
16 if color[y] = BLACK  
17    then RB-DELETE-FIXUP(T, x)  
18 return y  

RB-DELETE-FIXUP(T, x) 恢复与保持红黑性质的工作:

 1 while x ≠ root[T] and color[x] = BLACK  
 2     do if x = left[p[x]]  
 3           then w ← right[p[x]]  
 4                if color[w] = RED  
 5                   then color[w] ← BLACK                        ▹  Case 1  
 6                        color[p[x]] ← RED                       ▹  Case 1  
 7                        LEFT-ROTATE(T, p[x])                    ▹  Case 1  
 8                        w ← right[p[x]]                         ▹  Case 1  
 9                if color[left[w]] = BLACK and color[right[w]] = BLACK  
10                   then color[w] ← RED                          ▹  Case 2  
11                        x ← p[x]                                ▹  Case 2  
12                   else if color[right[w]] = BLACK  
13                           then color[left[w]] ← BLACK          ▹  Case 3  
14                                color[w] ← RED                  ▹  Case 3  
15                                RIGHT-ROTATE(T, w)              ▹  Case 3  
16                                w ← right[p[x]]                 ▹  Case 3  
17                         color[w] ← color[p[x]]                 ▹  Case 4  
18                         color[p[x]] ← BLACK                    ▹  Case 4  
19                         color[right[w]] ← BLACK                ▹  Case 4  
20                         LEFT-ROTATE(T, p[x])                   ▹  Case 4  
21                         x ← root[T]                            ▹  Case 4  
22        else (same as then clause with "right" and "left" exchanged)  
23 color[x] ← BLACK  

“在删除结点后，原红黑树的性质可能被改变，如果删除的是红色结点，那么原红黑树的性质依旧保持，此时不用做修正操作，如果删除的结点是黑色结点，原红黑树的性质可能会被改变，我们要对其做修正操作。那么哪些树的性质会发生变化呢，如果删除结点不是树唯一结点，那么删除结点的那一个支的到各叶结点的黑色结点数会发生变化，此时性质5被破坏。如果被删结点的唯一非空子结点是红色，而被删结点的父结点也是红色，那么性质4被破坏。如果被删结点是根结点，而它的唯一非空子结点是红色，则删除后新根结点将变成红色，违背性质2。”

“上面的修复情况看起来有些复杂，下面我们用一个分析技巧：我们从被删结点后来顶替它的那个结点开始调整，并认为它有额外的一重黑色。这里额外一重黑色是什么意思呢，我们不是把红黑树的结点加上除红与黑的另一种颜色，这里只是一种假设，我们认为我们当前指向它，因此空有额外一种黑色，可以认为它的黑色是从它的父结点被删除后继承给它的，它现在可以容纳两种颜色，如果它原来是红色，那么现在是红+黑，如果原来是黑色，那么它现在的颜色是黑+黑。有了这重额外的黑色，原红黑树性质5就能保持不变。现在只要恢复其它性质就可以了，做法还是尽量向根移动和穷举所有可能性。"–saturnman。

如果是以下情况，恢复比较简单：

• 当前节点是红+黑色
  解法：直接把当前节点染成黑色，结束时红黑树性质全部恢复。
• 当前节点是黑+黑且是根节点
  解法：什么都不做
  
  如果是以下情况呢？
• 删除修复情况1：当前节点是黑+黑且兄弟节点为红色（此时父节点和兄弟节点的子节点分为黑）
• 删除修复情况2：当前节点是黑+黑且兄弟是黑色且兄弟的两个子节点全为黑色
• 删除修复情况3：当前节点是黑+黑，兄弟节点是黑色，兄弟左子为红，右子为黑
• 删除修复情况4：当前节点是黑+黑，兄弟节点是黑色，兄弟右子为红，左子任意。

删除修复情况1：当前结点是黑+黑且兄弟结点为红色(此时父结点和兄弟结点的子结点分为黑)。(case 1)
解法：把父结点染成红色，把兄弟结点染成黑色，之后重新进入算法（我们只讨论当前结点是其父结点左孩子时的情况）。此变换后原红黑树性质5不变，而把问题转化为兄弟结点为黑色的情况(注：变化前，原本就未违反性质5，只是为了把问题转化为兄弟结点为黑色的情况)。

变化前：

变化后：

删除修复情况2：当前结点是黑加黑且兄弟是黑色且兄弟结点的两个子结点全为黑色。
解法：把当前结点和兄弟结点中抽取一重黑色追加到父结点上，把父结点当成新的当前结点，重新进入算法。（此变换后性质5不变）

变化前：

变化后：

删除修复情况3：当前结点颜色是黑+黑，兄弟结点是黑色，兄弟的左子是红色，右子是黑色。

解法：把兄弟结点染红，兄弟左子结点染黑，之后再在兄弟结点为支点解右旋，之后重新进入算法。此是把当前的情况转化为情况4，而性质5得以保持
变化前：

变化后：

删除修复情况4：当前结点颜色是黑-黑色，它的兄弟结点是黑色，但是兄弟结点的右子是红色，兄弟结点左子的颜色任意。

解法：把兄弟结点染成当前结点父结点的颜色，把当前结点父结点染成黑色，兄弟结点右子染成黑色，之后以当前结点的父结点为支点进行左旋，此时算法结束，红黑树所有性质调整正确

变化前：

变化后：

建议阅读：http://www.cs.princeton.edu/~rs/talks/LLRB/RedBlack.pdf