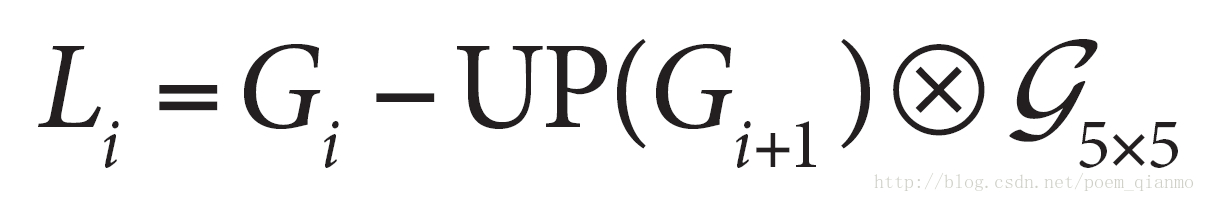opencv图像处理学习（二十五）——卷积与图像金字塔

1.图像卷积

图像掩码操作一节中指出图像卷积实际计算的是图像相关性，而非卷积操作。基于傅立叶变换理论是将时域内信号变换成频域内信号，对应关系为将时域的卷积操作转换为频域内的乘积操作。图像低频分量表示背景和缓慢变化区域，高频分量是通过图像的边缘、细节及相关操作。对于频谱分析，提取高频分量是通过傅立叶逆变换锐化操作的，提取低频分量是通过傅立叶逆变换模糊操作的。根据傅立叶变换理论，频域内的频谱值都是由整个图像求出来的，因此在整个频谱范围内，低频分量集中于四个角中。图像卷积操作如下式所示：

$F(f*g)=F(f).F(g)$

上式指出两个函数的卷积的傅立叶变换等于各自傅立叶变换的乘积，根据卷积定理两个函数的卷积可以通过对两个函数的傅立叶变换的乘积在进行傅立叶反变换得到，如下式反变换

$f*g=F^{-1}({F(f).F(g)})$

在进行图像卷积运算时，一般是将卷积核算子沿着图像从左到右从上到下计算每一个像素处与核算子模版卷积后的值，即将函数f与模板g的定义域相交的元素进行乘积并求和（对应位置元素相乘相加），对边缘点要进行特殊处理操作（边缘外处补0），因此这种操作时间复杂度较高，而采用傅立叶变换的方法可以提高运算效率。图像卷积操作广泛应用在图像滤波技术中。

PS：二维卷积： $F(u,v)=f(x,y)*g(x,y)=\int \int f(x,y)g(u-x,v-y)$

opencv自带函数看第二十三章。

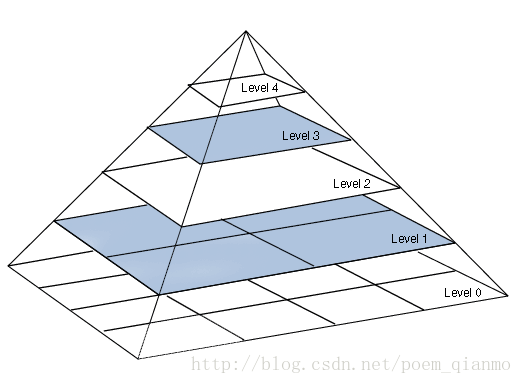
2.图像金字塔

图像金字塔是一系列图像的集合，所有多个分辨率的图像来源于同一原始图像，常用于图像缩放或图像分割中。图像金字塔结构是用于多分辨率处理的一种图像存储数据结构，向下采样技术是高斯金字塔，向上重建技术是拉普拉斯金字塔。

扫描二维码关注公众号，回复： 5763823 查看本文章

在opencv中，提供了对图像金字塔的实现的pyrUp和pyrDown函数用于向上和向下采样。

void pyrDown(InputArray src,OutputArray dst,const Size& dstsize = Size(),int borderType = BORDER_DEFAULT);

参数src表示源图像，dst表示输出图像，dstsize表示输出图像的大小，提供的默认参数用Size（（src.cols+1）/2,（src.rows+1）/2）来计算，默认参数的情况下需满足条件|dstsize.width*2-src.cols|≤2及|dstsize.height*2-src.rows|≤2

void pyrUp(InputArray src,OutputArray dst,const Size& dstsize = Size(),int borderType = BORDER_DEFAULT);

（1）高斯金字塔

<1>高斯核

径向基函数是一个取值仅仅依赖于离原点距离的实值函数，也就是Φ（x）=Φ(‖x‖),或者还可以是到任意一点c的距离，c点称为中心点，也就是Φ（x，c）=Φ(‖x-c‖)。任意一个满足Φ（x）=Φ(‖x‖)特性的函数Φ都叫做径向基函数，标准的一般使用欧氏距离（也叫做欧式径向基函数），尽管其他距离函数也是可以的。

PS：高斯公式： $Gussa(x,y)=\frac{1}{2\pi \sigma ^{2}}e^\frac{{-(x^{2}+y^{2})}}{2\sigma ^{2}}$ （二维）

要构建复杂的非线性模型，往往是从简单的线性模型出发的。线性模型很棒，因为它们易于理解且易于优化。缺点是因为他们只能学习非常简单的决策边界。神经网络可以学习更复杂的决策边界，但会丢失许多线性模型的漂亮凸性。使线性模型表现为非线性的一种方法是转换输入，这就是核方法。

综上所述，所谓径向基函数 (Radial Basis Function 简称 RBF), 就是某种沿径向对称的标量函数。通常定义为空间中任一点x到某一中心xc之间欧氏距离的单调函数 , 可记作 k(||x-xc||), 其作用往往是局部的 , 即当x远离xc时函数取值很小。最常用的径向基函数是高斯核函数 ,形式为 $k(||x-x_{c}||)=e^{-\frac{||x-x_{c}||^{2}}{2\sigma ^{2}}}$ ，其中xc为核函数中心,σ为函数的宽度参数 , 控制了函数的径向作用范围。

现在有了高斯核函数的基础，我们来了解一下权重矩阵。

取 $\sigma =1.1105$ ,则有 $\begin{bmatrix} e^{\frac{\sqrt{(-2-0)^{2}+(2-0)^{2})}}{2\sigma ^{2}}}& e^{\frac{\sqrt{(-1-0)^{2}+(2-0)^{2})}}{2\sigma ^{2}}}& e^{\frac{\sqrt{(0-0)^{2}+(2-0)^{2})}}{2\sigma ^{2}}} & e^{\frac{\sqrt{(1-0)^{2}+(2-0)^{2})}}{2\sigma ^{2}}} &e^{\frac{\sqrt{(2-0)^{2}+(2-0)^{2})}}{2\sigma ^{2}}} \\ e^{\frac{\sqrt{(-2-0)^{2}+(1-0)^{2})}}{2\sigma ^{2}}}& e^{\frac{\sqrt{(-1-0)^{2}+(1-0)^{2})}}{2\sigma ^{2}}} & e^{\frac{\sqrt{(0-0)^{2}+(1-0)^{2})}}{2\sigma ^{2}}} & e^{\frac{\sqrt{(1-0)^{2}+(1-0)^{2})}}{2\sigma ^{2}}} & e^{\frac{\sqrt{(2-0)^{2}+(1-0)^{2})}}{2\sigma ^{2}}}\\ e^{\frac{\sqrt{(-2-0)^{2}+(0-0)^{2})}}{2\sigma ^{2}}} & e^{\frac{\sqrt{(-1-0)^{2}+(0-0)^{2})}}{2\sigma ^{2}}}& e^{\frac{\sqrt{(0-0)^{2}+(0-0)^{2})}}{2\sigma ^{2}}} &e^{\frac{\sqrt{(1-0)^{2}+(0-0)^{2})}}{2\sigma ^{2}}} &e^{\frac{\sqrt{(2-0)^{2}+(0-0)^{2})}}{2\sigma ^{2}}} \\ & e^{\frac{\sqrt{(-1-0)^{2}+(-1-0)^{2})}}{2\sigma ^{2}}} &e^{\frac{\sqrt{(0-0)^{2}+(-1-0)^{2})}}{2\sigma ^{2}}} & \cdots & \\ & &\cdots & & \end{bmatrix}$ ，约简得 $\begin{bmatrix} 1 &4 & 6 &4 &1 \\ 4&16 & 24 &16 &4 \\ 6&24 & 36 &24 &6 \\ 4&16 & 24 & 16 &4 \\ 1& 4 &6 & 4 & 1 \end{bmatrix}$

这25个点的权重总和等于256，如果只计算这25个点的加权平均，还必须让它们的权重之和等于1，因此上面25个值还要分别除以256，得到最终的权重矩阵，即 $\delta =\frac{1}{256}\begin{bmatrix} 1 &4 &6 & 4 &1 \\ 4& 16 & 24 &16 & 4\\ 6& 24 & 36 & 24 &6 \\ 4 &16 & 24 &16 &4 \\ 1 & 4& 6 & 4 &1 \end{bmatrix}$ ，这是最常见的高斯核函数取值。

然后现在有0-255的像素矩阵： $\begin{bmatrix} 0 &255 &1 & 255 & 23\\ 5 &34 &33 & 22 & 77\\ 46& 87 & 231 & 134 &178 \\ 0& 99 & 111 & 222 &233 \\ 156 & 165 & 133 &122 &111 \end{bmatrix}$ ，则卷积过后（打起来太麻烦了）为就是该中心点得到的像素值。

高斯金字塔的生成过程包含高斯核卷积核下采样过程，设源图像为 $G_{0}(x,y)$ ,分辨率为M x N， $G_{0}$ 表示高斯金字塔的最底层为第0层，即与原图像相同。为得到高斯金字塔层数 $G_{i+1}$ 图像，首先对源图像 $G_{i}$ 进行高斯内核卷积，然后删除所有偶数行列，直到只剩一个值。

对生成核的限制既能保证低通的性质，又能保持图像缩放扩后的亮度平滑，不出现边界缝隙。

（2）拉普拉斯金字塔

拉普拉斯金字塔操作实现向上重建图像，对 $G_{i}$ 内插得到放大图像 $G_{i}^{*}$ ，使 $G_{i}^{*}$ 的尺寸与 $G_{i-1}$ 的尺寸相同，可表达为下式：

$G_{i}^{*}(x,y)=4\sum_{m=-2}^{2}\sum_{n=-2}^{2}w(m,n)G_{i}(\frac{x+m}{2},\frac{y+n}{2})$

其中i的取值范围为(0,N)。对于上式中的 $G_{i}^{*}(\frac{x+m}{2},\frac{y+n}{2})$ ，当且 $\frac{x+m}{2}$ 与 $\frac{y+n}{2}$ 为整数时可变换为 $G_{i}(\frac{x+m}{2},\frac{y+n}{2})$ ，其他情况下均为零。

通过上式中的插值运算可以把金字塔的第i级图像扩大到i-1级同尺度，可定义为当i的取值范围[0,N)满足 $LP_{i}=G_{i}-G_{i+1}^{*}$ ，当i=N时满足 $LP_{N}= G_{N}$ ,N为拉普拉斯金字塔塔顶的层号， $LP_{i}$ 是拉普拉斯金字塔分解的第i层图像。拉普拉斯金字塔实际就是高斯金字塔与其上一层通过差值扩大的插值图像，上层图像是下层低通滤波后下采样得到的，扩大后与原级的插值反映的是高斯金字塔两级建的信息差，此步骤类似于带通滤波，最终拉普拉斯金字塔也表现出同级高斯金字塔的高频分量（细节部分）。

PS：

下式是拉普拉斯金字塔第i层的数学定义：

式中的表示第i层的图像。而UP（）操作是将源图像中位置为(x,y)的像素映射到目标图像的(2x+1,2y+1)位置，即在进行向上取样。符号表示卷积，为5x5的高斯内核。

该式子实现两个步骤：在偶数行和列插入0，然后使用下采样中的高斯核进行滤波处理，得到和l-1层一样大小的图像。

e.g:

$\begin{bmatrix} 3 & 44 &54 \\ 145& 167 & 233\\ 77 &11 &6 \end{bmatrix}->\begin{bmatrix} a_{00} & a_{01} &a_{02} \\ a_{10}& a_{11} & a_{12}\\ a_{20}& a_{21} & a_{22} \end{bmatrix}->\begin{bmatrix} a_{00} & 0 &a_{01} & 0 &a_{02} \\ 0 & 0 & 0 & 0 &0 \\ a_{10}&0 & a_{11} &0 & a_{12}\\ 0 & 0 & 0 &0 &0 \\ a_{20}&0 & a_{21} &0 &a_{22} \end{bmatrix}*\delta$

N为拉普拉斯金字塔顶层的层号LPl是拉普拉斯金字塔分解的第L层图像。由LP0，LP1、LP2…LPN构成的金字塔即为拉普拉斯金字塔。它的每一层L0图像是高斯金字塔本层G0图像与其高一层图像G1经内插放大后图像*G1的差，此过程相当于带通滤波，因此拉普拉斯金字塔又称为带通金字塔分解。

opencv图像处理学习（二十五）——卷积与图像金字塔

猜你喜欢