1.前言
和树的遍历类似,图的遍历也是从图中某点出发,然后按照某种方法对图中所有顶点进行访问,且仅访问一次。
但是图的遍历相对树而言要更为复杂。因为图中的任意顶点都可能与其他顶点相邻,所以在图的遍历中必须记录已被访问的顶点,避免重复访问。
根据搜索路径的不同,我们可以将遍历图的方法分为两种:广度优先搜索和深度优先搜索。
2.深度优先搜索
2.1算法的基本思路
深度优先搜索类似于树的先序遍历,具体过程如下:
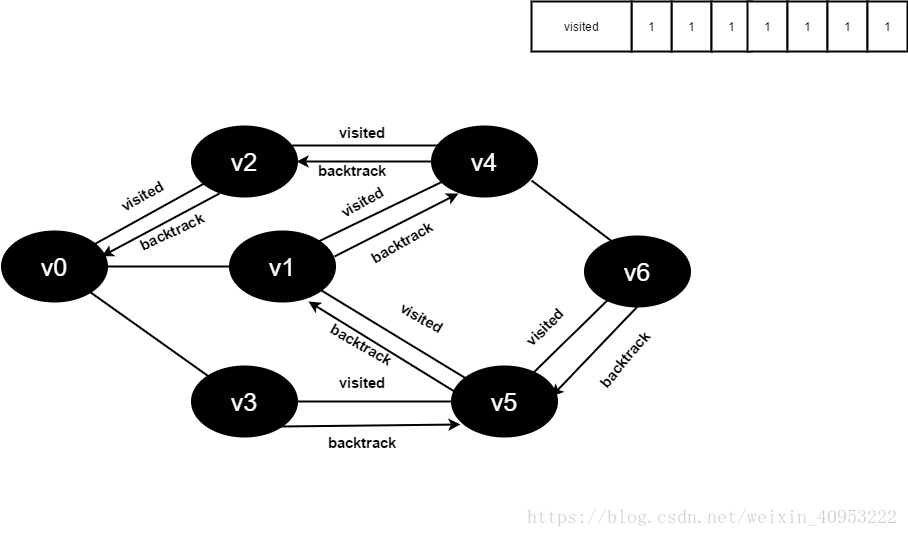
准备工作:创建一个visited数组,用于记录所有被访问过的顶点。
1.从图中v0出发,访问v0。
2.找出v0的第一个未被访问的邻接点,访问该顶点。以该顶点为新顶点,重复此步骤,直至刚访问过的顶点没有未被访问的邻接点为止。
3.返回前一个访问过的仍有未被访问邻接点的顶点,继续访问该顶点的下一个未被访问领接点。
4.重复2,3步骤,直至所有顶点均被访问,搜索结束。
2.2算法的实现过程
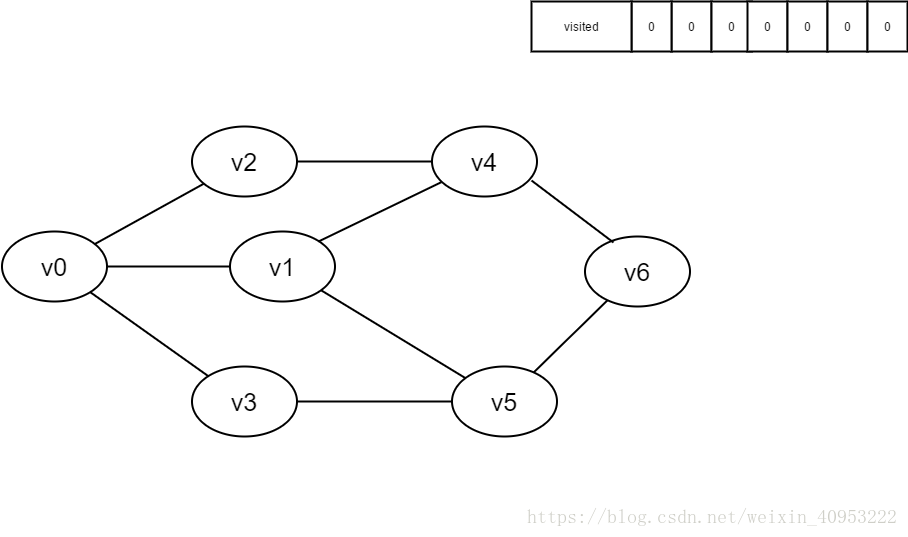
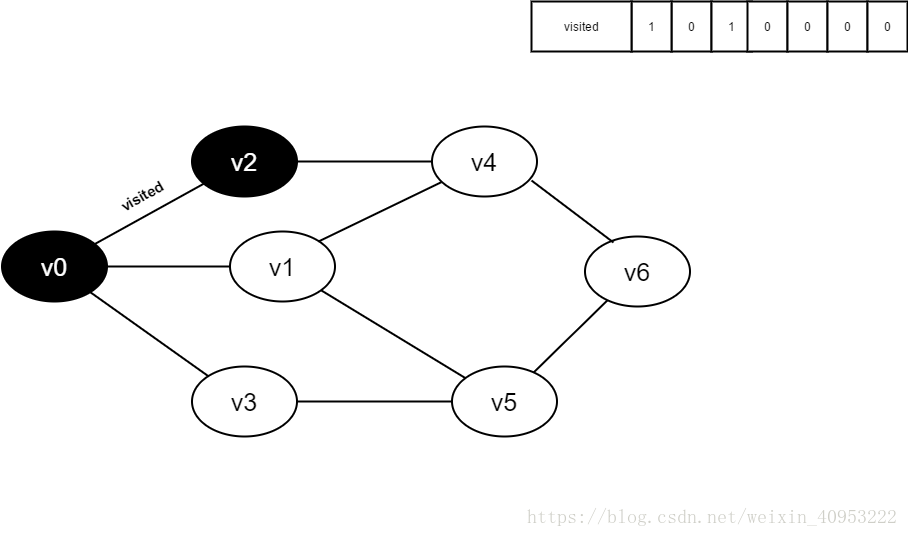
初始时所有顶点均未被访问,visited数组为空。
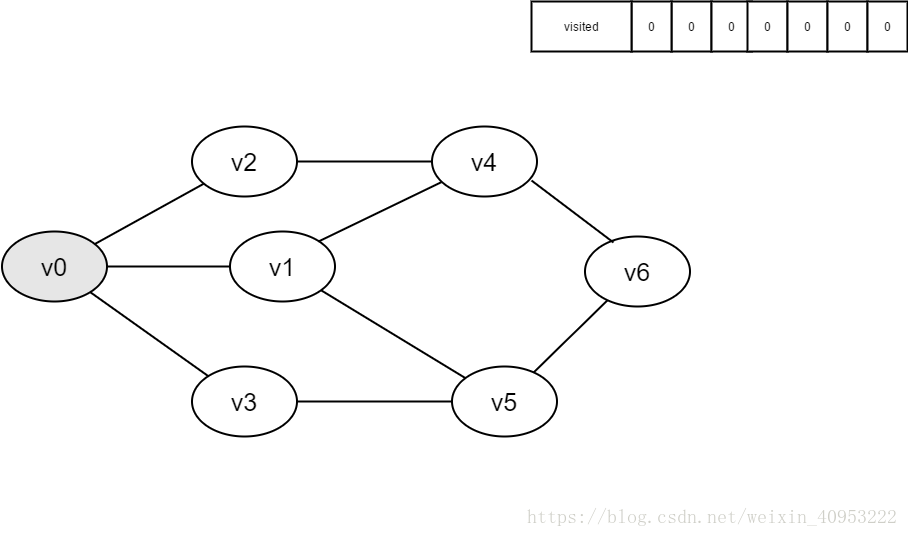
即将访问v0。
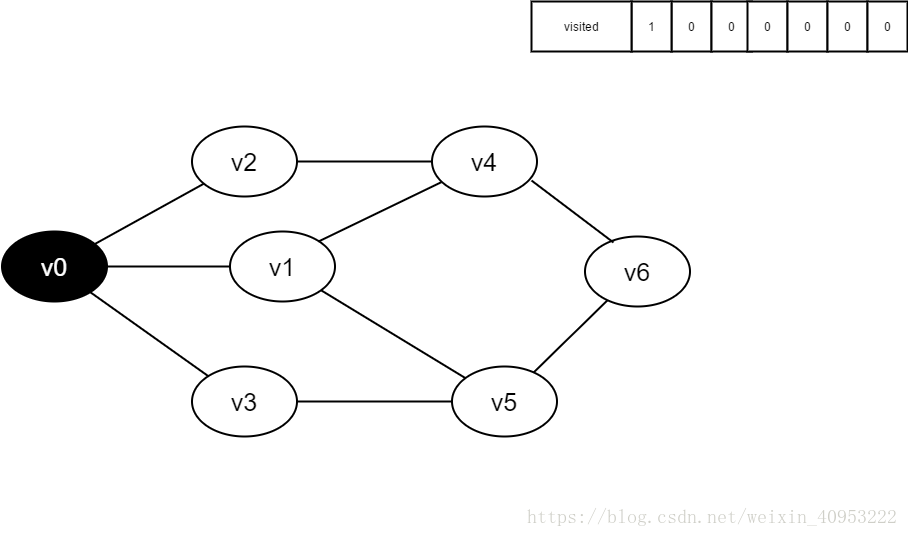
访问v0,并将visited[0]的值置为1。
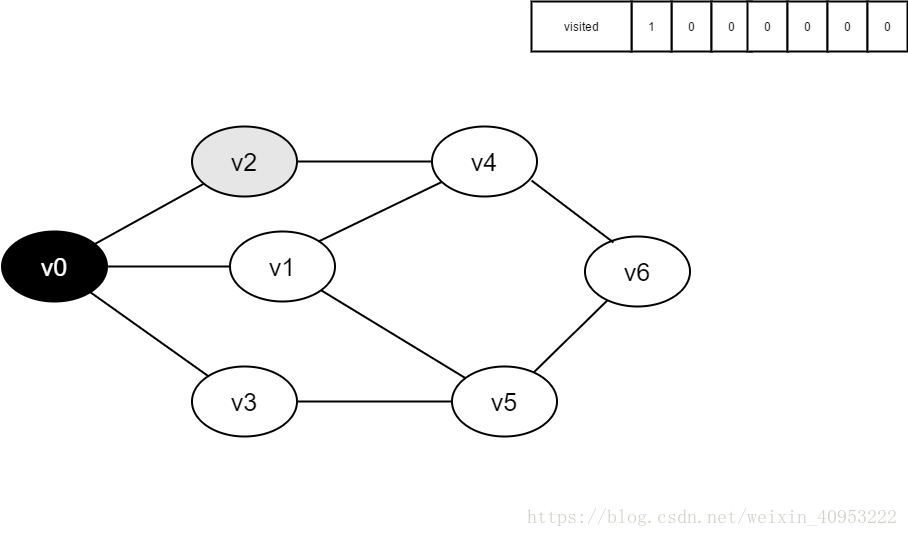
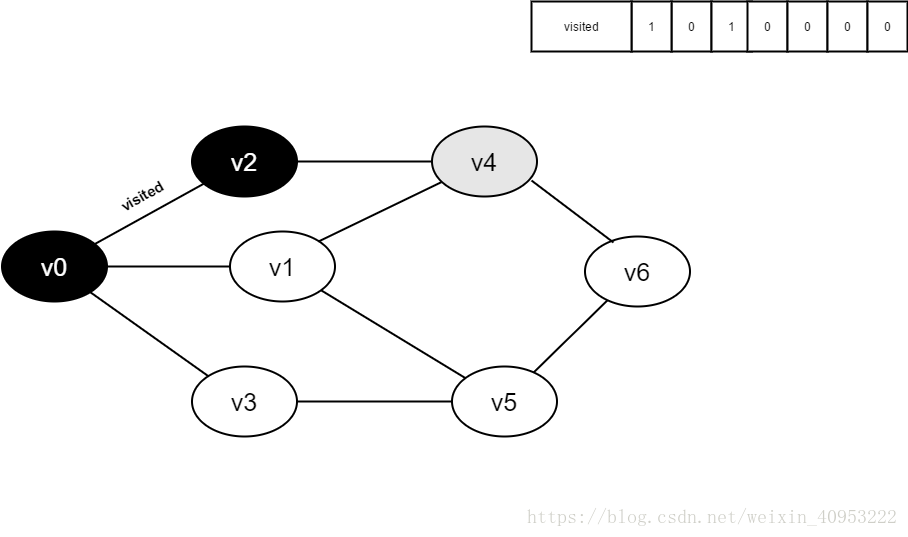
4.访问v0的邻接点v2,判断visited[2],因其值为0,访问v2。
将visited[2]置为1。
访问v2的邻接点v0,判断visited[0],其值为1,不访问。
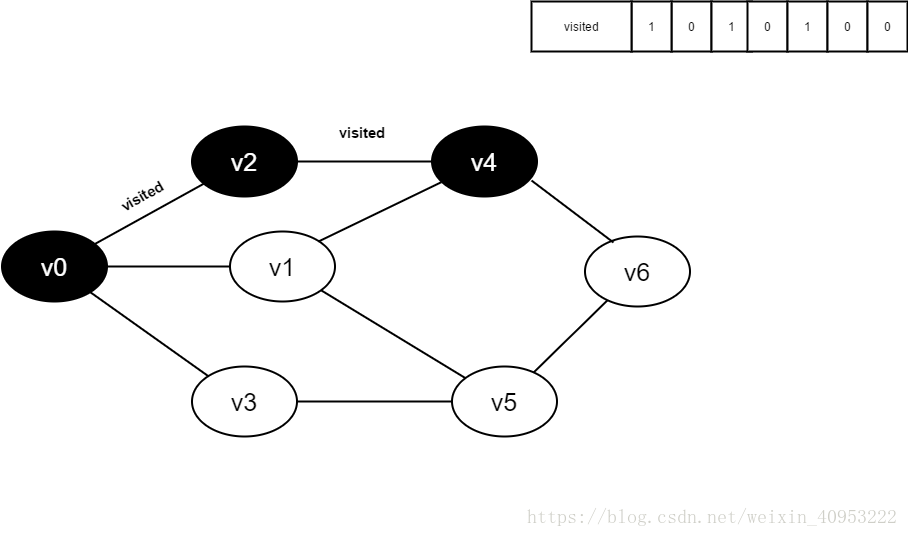
继续访问v2的邻接点v4,判断visited[4],其值为0,访问v4。
将visited[4]置为1。
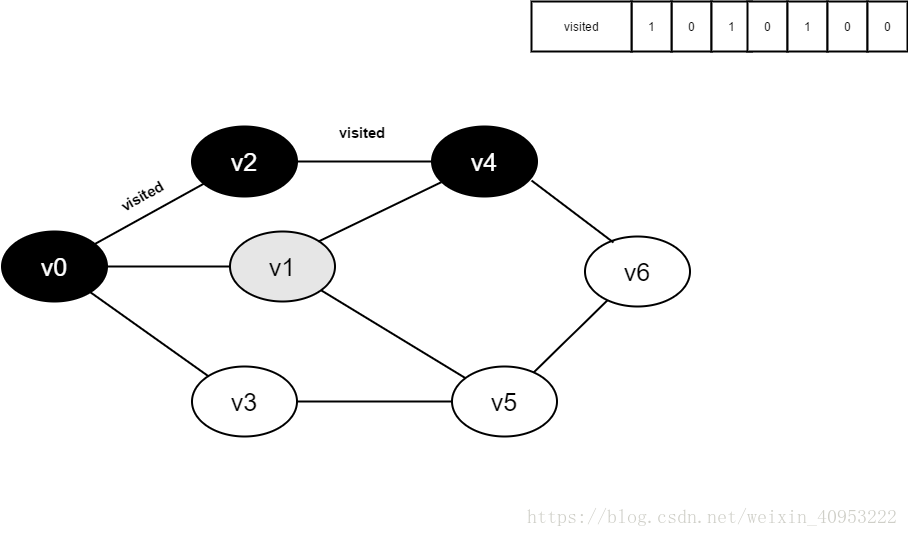
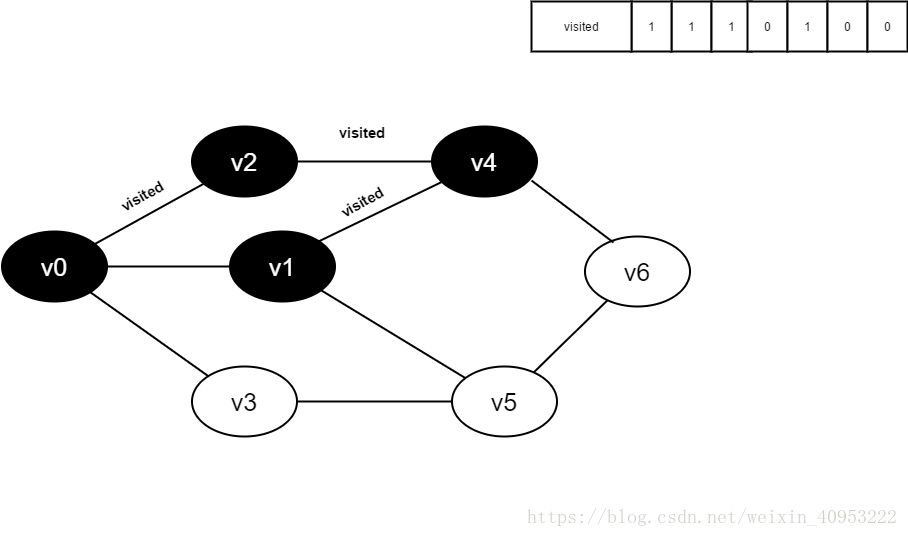
访问v4的邻接点v1,判断visited[1],其值为0,访问v1。
将visited[1]置为1。
访问v1的邻接点v0,判断visited[0],其值为1,不访问。
继续访问v1的邻接点v4,判断visited[4],其值为1,不访问。
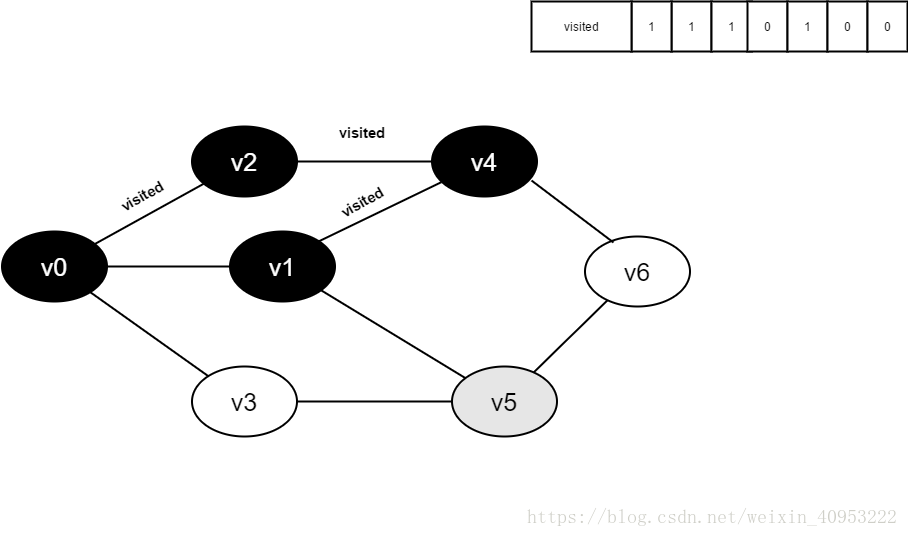
继续访问v1的邻接点v5,判读visited[5],其值为0,访问v5。
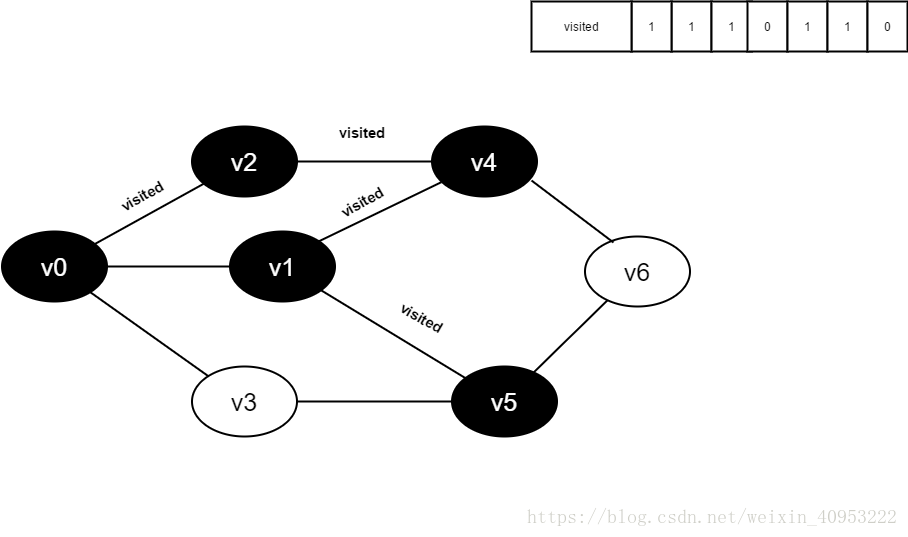
将visited[5]置为1。
访问v5的邻接点v1,判断visited[1],其值为1,不访问。
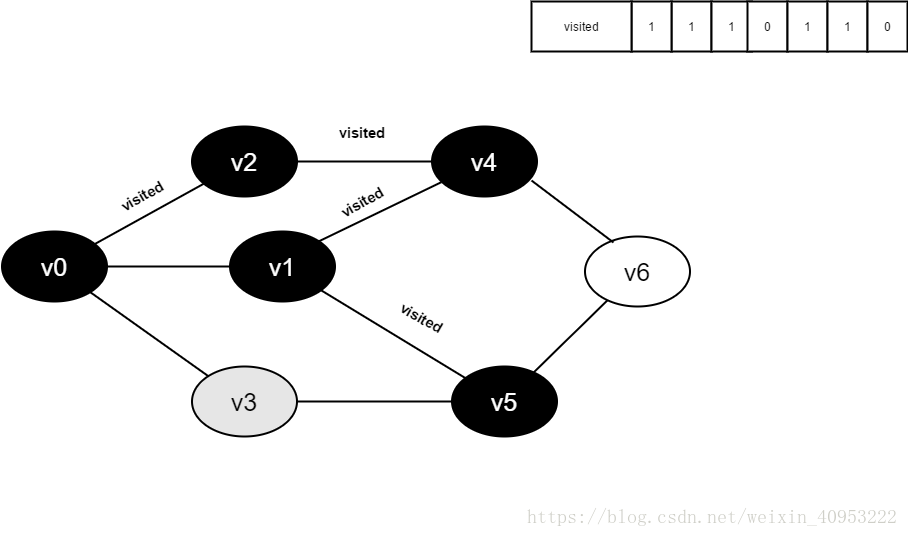
继续访问v5的邻接点v3,判断visited[3],其值为0,访问v3。
将visited[1]置为1。
15.将visited[6]置为1。
访问v3的邻接点v0,判断visited[0],其值为1,不访问。
继续访问v3的邻接点v5,判断visited[5],其值为1,不访问。
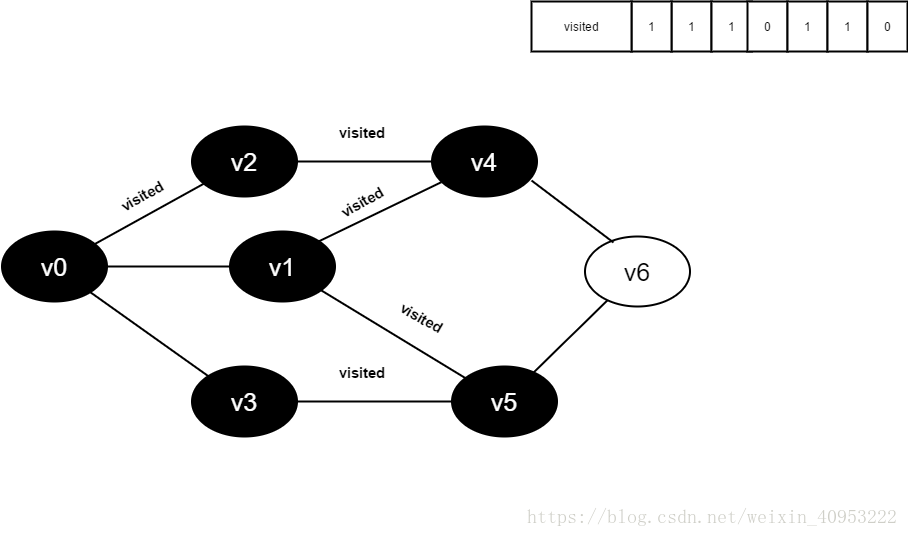
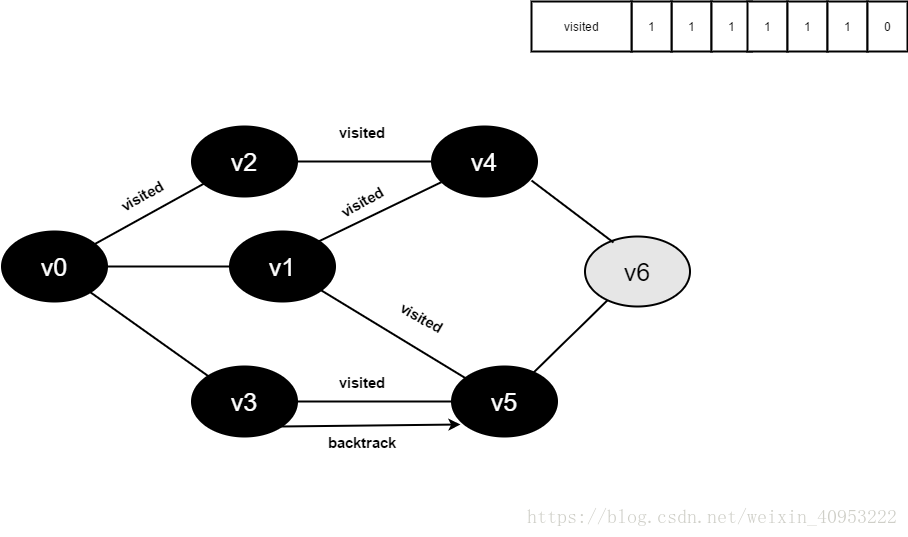
v3所有邻接点均已被访问,回溯到其上一个顶点v5,遍历v5所有邻接点。
访问v5的邻接点v6,判断visited[6],其值为0,访问v6。
访问v6的邻接点v4,判断visited[4],其值为1,不访问。
访问v6的邻接点v5,判断visited[5],其值为1,不访问。
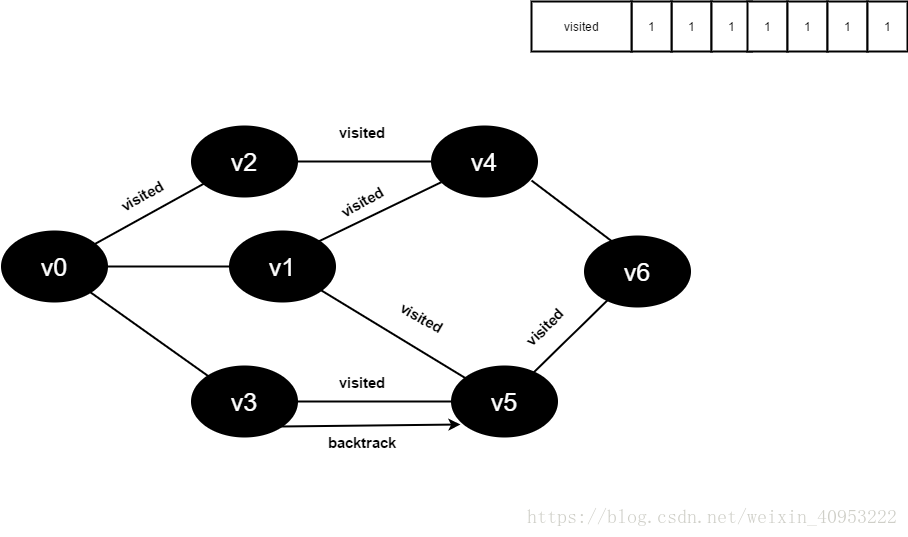
v6所有邻接点均已被访问,回溯到其上一个顶点v5,遍历v5剩余邻接点。
v5所有邻接点均已被访问,回溯到其上一个顶点v1。
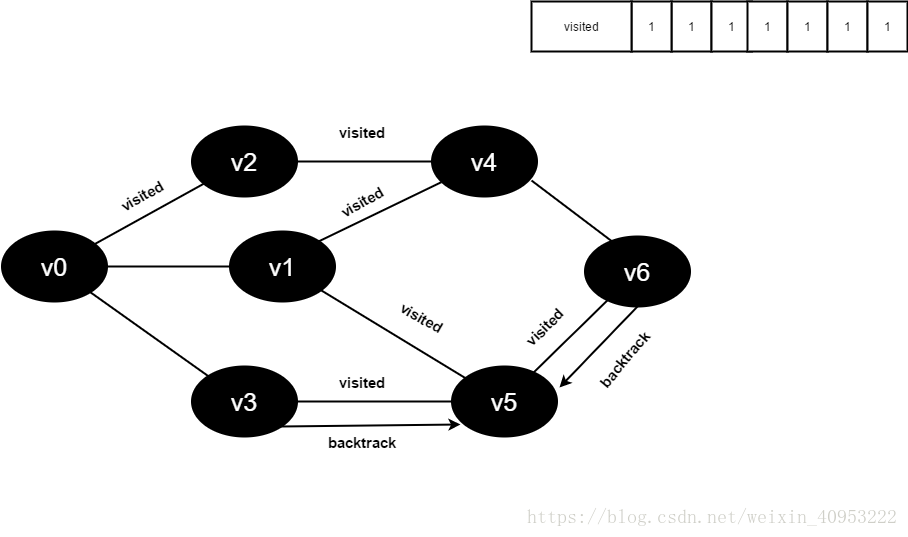
v1所有邻接点均已被访问,回溯到其上一个顶点v4,遍历v4剩余邻接点v6。
v4所有邻接点均已被访问,回溯到其上一个顶点v2。
v2所有邻接点均已被访问,回溯到其上一个顶点v1,遍历v1剩余邻接点v3。
v1所有邻接点均已被访问,搜索结束。
2.3具体代码实现
2.3.1用邻接矩阵表示图的深度优先搜索
邻接矩阵的创建在上述已描述过,这里不再赘述
void DFS_AM(AMGraph &G, int v)
{
int w;
printf("%c ", G.vexs[v]);
visited[v] = 1;
for (w = 0; w < G.vexnum; w++)
if (G.arcs[v][w]&&!visited[w]) //递归调用
DFS_AM(G,w);
}
2.3.2用邻接表表示图的深度优先搜素
邻接表的创建在上述已描述过,这里不再赘述。
void DFS_AL(ALGraph &G, int v)
{
int w;
printf("%c ", G.vertices[v].data);
visited[v] = 1;
ArcNode *p = new ArcNode;
p = G.vertices[v].firstarc;
while (p)
{
w = p->adjvex;
if (!visited[w]) DFS_AL(G, w);
p = p->nextarc;
}
}3.广度优先搜索
3.1.算法的基本思路
常常我们有这样一个问题,从一个起点开始要到一个终点,我们要找寻一条最短的路径,从图2-1举例,如果我们要求V0到V6的一条最短路(假设走一个节点按一步来算),我们明显看出这条路径就是V0->V2->V6,而不是V0->V3->V5->V6。先想想你自己刚刚是怎么找到这条路径的:首先看跟V0直接连接的节点V1、V2、V3,发现没有V6,进而再看刚刚V1、V2、V3的直接连接节点分别是:{V0、V4}、{V0、V1、V6}、{V0、V1、V5}(这里画删除线的意思是那些顶点在我们刚刚的搜索过程中已经找过了,我们不需要重新回头再看他们了)。这时候我们从V2的连通节点集中找到了V6,那说明我们找到了这条V0到V6的最短路径:V0->V2->V6,虽然你再进一步搜索V5的连接节点集合后会找到另一条路径V0->V3->V5->V6,但显然他不是最短路径。
我们采用示例图来说明这个过程,在搜索的过程中,初始所有节点是白色(代表了所有点都还没开始搜索),把起点V0标志成灰色(表示即将访问V0),下一步搜索的时候,我们把所有的灰色节点访问一次,然后将其变成黑色(表示已经被访问过了),进而再将他们所能到达的节点标志成灰色(因为那些节点是下一步搜索的目标点了),但是这里有个判断,就像刚刚的例子,当访问到V1节点的时候,它的下一个节点应该是V0和V4,但是V0已经在前面被染成黑色了,所以不会将它染灰色。这样持续下去,直到目标节点V6被染灰色,说明了下一步就到终点了,没必要再搜索(染色)其他节点了,此时可以结束搜索了,整个搜索就结束了。然后根据搜索过程,反过来把最短路径找出来,图3-1中把最终路径上的节点标志成绿色。
整个过程的实例图如下图所示。

初始全部都是白色(未访问)

即将搜索起点V0(灰色)

已搜索V0,即将搜索V1、V2、V3

……终点V6被染灰色,终止

找到最短路径
3.2.广度优先搜索流程图

3.3.实例
说到广度优先搜索,大家可能先想到的是广度优先遍历,其实广度优先搜索就是利用了广度优先遍历的一种搜索算法。我个人总结的该算法包含以下几个关键点,掌握了这几个点,该算法也就掌握的很好了。下面也基本上是围绕这几个关键点展开的。
1.状态
2.状态转移方式
3.有效状态
4.队列
5.标记
这里我们便可以看到一个点加上一个时间t便构成了一个所谓的状态,而我们广度优先搜素就是要按层,一层一层地搜索这些状态,直到找到要求状态为止。上面的图我们还应该修改修改,因为,第二次到达的点所需要的时间肯定比第一次到达所需要的时间多,如上图的(0,0,3),所以,我们设置一个标记,凡是我们到达过的点,便不进行第二次的搜索与延伸,此之谓剪枝,这样一来状态的总数便等于A*B(A为总行数,B为总列数),只要这个时间复杂度在我们的接受范围之内,我们便可以采用广度优先搜索。
状态转移呢,是指由一个状态可以延伸出其他哪些状态,也就是可以往哪些地方走的问题。
对应于题目的输入数组:
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};
我们把节点定义为(x,y),(x,y)表示数组maze的项maze[x][y],于是起点就是(0,0),终点是(4,4)。按照刚刚的思路,我们大概手工梳理一遍:
初始条件:
起点Vs为(0,0),终点Vd为(4,4),灰色节点集合Q={}
初始化所有节点为白色节点,开始我们的广度搜索!
手工执行步骤:
1.起始节点Vs变成灰色,加入队列Q,Q={(0,0)}
2.取出队列Q的头一个节点Vn,Vn={0,0},Q={}
3.把Vn={0,0}染成黑色,取出Vn所有相邻的白色节点{(1,0)}
4.不包含终点(4,4),染成灰色,加入队列Q,Q={(1,0)}
5.取出队列Q的头一个节点Vn,Vn={1,0},Q={}
6.把Vn={1,0}染成黑色,取出Vn所有相邻的白色节点{(2,0)}
7.不包含终点(4,4),染成灰色,加入队列Q,Q={(2,0)}
8.取出队列Q的头一个节点Vn,Vn={2,0},Q={}
9.把Vn={2,0}染成黑色,取出Vn所有相邻的白色节点{(2,1), (3,0)}
10.不包含终点(4,4),染成灰色,加入队列Q,Q={(2,1), (3,0)}
11.取出队列Q的头一个节点Vn,Vn={2,1},Q={(3,0)}
12. 把Vn={2,1}染成黑色,取出Vn所有相邻的白色节点{(2,2)}
13.不包含终点(4,4),染成灰色,加入队列Q,Q={(3,0), (2,2)}
14.持续下去,知道Vn的所有相邻的白色节点中包含了(4,4)……
15.此时获得了答案
起始你很容易模仿上边过程走到终点,那为什么它就是最短的呢?怎么保证呢?我们来看看广度搜索的过程中节点的顺序情况:

你是否观察到了,广度搜索的顺序是什么样子的?
图中标号即为我们搜索过程中的顺序,我们观察到,这个搜索顺序是按照上图的层次关系来的,例如节点(0,0)在第1层,节点(1,0)在第2层,节点(2,0)在第3层,节点(2,1)和节点(3,0)在第3层。
我们的搜索顺序就是第一层->第二层->第三层->第N层这样子。
我们假设终点在第N层,因此我们搜索到的路径长度肯定是N,而且这个N一定是所求最短的。
我们用简单的反证法来证明:假设终点在第N层上边出现过,例如第M层,M<N,那么我们在搜索的过程中,肯定是先搜索到第M层的,此时搜索到第M层的时候发现终点出现过了,那么最短路径应该是M,而不是N了。
所以根据广度优先搜索的话,搜索到终点时,该路径一定是最短的。说了这么多,是时候上点干货了,我们看看代码。
#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int> Pair;
const int INF = 0x3f3f3f3f;
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};
int dx[] = {1, 0, -1, 0};
int dy[] = {0, 1, 0, -1};
int d[5][5];
int main()
{
memset(d, 0x3f, sizeof(d));
queue<Pair> que;
que.push(Pair(0,0)); // 将起点入队
d[0][0] = 0; //把起点设置为0
while(que.size()) {
Pair p = que.front();
que.pop();
if(p.first == 5 && p.second == 5) break;
for(int i=0; i < 4; i++) {
int x = p.first + dx[i];
int y = p.second + dy[i];
if(x>=0 && x<5 && y>=0 && y<5 && maze[x][y]==0 && d[x][y]==INF) {
que.push(Pair(x,y));
d[x][y] = d[p.first][p.second] + 1;
}
}
}
cout << d[4][4] << endl;
return 0;
}#include<iostream>
#include<queue>
using namespace std;
int map[5][5]; //保存迷宫图
bool flag[5][5];//标记改点是否到达过
int R[4][2]={ //用于状态扩展
-1,0, 1,0, 0,-1, 0,1
};
// 定义类
struct Stat {
int x, y;
int cnt; // 步数
Stat* perv; //用于逆向寻找路径
Stat() {}
Stat(int x, int y, int cnt, Stat* perv) {
this->x = x;
this->y = y;
this->cnt = cnt;
this->perv = perv;
}
};
/**
* 广度优先搜索
* @return 终点状态
*/
Stat* bfs() {
queue<Stat*> q;
Stat* start = new Stat(0,0,0,NULL);
q.push(start);
while(!q.empty()) {
Stat* temp = q.front();
q.pop();
//这里就是状态的扩展,向上下左右四个方向扩展
for(int i=0;i<4;i++) {
int x = temp->x+R[i][0];
int y = temp->y+R[i][1];
//超出边界,便直接舍弃该状态
if(x<0 || y<0 || x>4 || y>4) continue;
//到达过该状态,也直接舍弃
if(flag[x][y] == true) continue;
//没有路,也直接舍弃
if(map[x][y] == 1) continue;
//创建新状态
Stat* tempS = new Stat(x, y, temp->cnt+1, temp);
//如果搜索到了目标状态,便返回
if(x == 4 && y == 4) {
return tempS;
}
q.push(tempS);
flag[x][y] = true;
}
}
return start;
}
/**
* 递归遍历输出
*/
void display(Stat* s) {
if(s->perv == NULL){
cout << "(0 , 0)" << endl;
return ;
}
display(s->perv);
cout << "(" << s->x << " , " << s->y << ")" << endl;
}
int main()
{
for(int i=0; i < 5; i++){
for(int j=0; j < 5; j++){
cin >> map[i][j];
flag[i][j] = false;
}
}
Stat* s = bfs();
cout << "count : " << s->cnt << endl;
display(s);
}总结
假设图有V个顶点,E条边,广度优先搜索算法需要搜索V个节点,因此这里的消耗是O(V),在搜索过程中,又需要根据边来增加队列的长度,于是这里需要消耗O(E),总得来说,效率大约是O(V+E)。
其实最影响BFS算法的是在于Hash运算,我们前面给出了一个visit数组,已经算是最快的Hash了,但有些题目来说可能Hash的速度要退化到O(lgn)的复杂度,当然了,具体还是看实际情况的。
文章转载自:
链接:https://blog.csdn.net/weixin_40953222/article/details/80544928