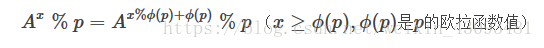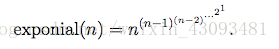取模运算
编程竞赛有相当一部分题目的数据结果过于庞大,往往需要对结果取模。例如(a*b) % p,若a*b的结果存储不了,再去取模,结果显然不对,为了防止溢出,可以分别对a取模,b取模,再求积取模。
取模运算公式:
加法:(a + b) % p = (a%p + b%p) % p
减法:(a - b) % p = ((a%p - b%p) + p) % p
乘法:(a * b) % p = (a%p)*(b%p) % p
幂运算:a ^ b % p = ((a % p)^b) % p
除法:(a / b) % p = (a%p * inv%p) % p
注意:(a / b) % p不能直接 / b 来求,需要找到一个数 inv 使得 inv * b % p= 1 。 我们称inv是逆元,下面介绍求逆元的方法。
由于在竞赛中,通常让我们把结果 % 1e9+7 ,所以推荐使用方法一。当然如果a刚好是b的倍数可以直接计算。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
// 方法一/方法二适用范围:mod为素数
// 方法一:递归求逆元
ll getInv(ll b) {
if(b==1) return 1;
return (mod-mod/b) * getInv(mod%b)%mod;
}
// 方法二:快速幂求逆元:根据费马小定理,(a/b)%mod = a*pow_mod(b,mod-2)%mod
// 快速幂原理举例:11二进制1011 ==> 11 = 2^0+2^1+2^3
// 2^11 = 2^(2^0) * 2^(2^1) * 2^(2^3)
ll pow_mod(ll x,ll n) {
ll res=1;
while(n > 0) {
if(n & 1) res = res*x % mod;
x = x*x % mod;
n >>= 1;
}
return res;
}
// 方法三:线性求逆元,可得到每个数对应的逆元
const int N = 100005;
long long inv[N];
void inv_init() {
inv[0] = inv[1] = 1;
for (int i = 2; i < N; i++) {
inv[i] = ((mod - mod/ i) * inv[mod % i]) % mod;
}
}
int main(){
ll a, b;
cin >> a >> b;
ll inv = getInv(b);
// ll inv = pow_mod(b, mod-2);
ll res = a%mod * inv%mod;
cout << res << endl;
return 0;
}大数取模的二进制方法
/*---------------------------------------------------
求 a^b mod c
把b化成二进制串的形式:b = (at at-1 at-2 … a1 a0)
那么有: b = at*2^t + at-1*2^(t-1) + … … + a1*2^1 + a0*2^0, 其中ai=0,1.
则:a^b mod c = a^( at*2^t + at-1*2^(t-1) + … … + a1*2^1 + a0*2^0) mod c =
((a^(a0*2^0) mod c) * a^(a1*2^1) mod c)… …
注意到:a^(2^(i+1))mod c = (a^(2^i) mod c)^2 mod c,
这样就可以在常数项时间内由2^i项推出2^(i+1)项。 时间复杂度为O((logb)^3).
----------------------------------------------------*/
int mod_exp(int a,int b0,int n) //return a^b0 % n
{
if( a > n ) a %= n;
int i, d = 1, b[35];
for( i=0; i < 35; ++i ) {
b[i] = b0 % 2;
b0 /= 2;
if( b0 == 0 ) break;
} //b[i]b[i-1]...b[0]为b0的二进制表示
for( ;i >= 0; --i ){
d = (d*d) % n;
if( b[i] == 1 ) d = (d*a)%n;
}
return d;
}快速幂
// n超过long long
typedef unsigned long long LL;
string str;
int input[10000005];
int output[10000005];
int len;
int sum=1,d=0,k=0;
void to_bin(string str) //将大整数转换为二进制,转换后为逆序
{
len=str.size();
for(int i=0;i<len;i++)
input[i]=str[i]-'0';
memset(output,0,sizeof(output));
sum=1,d=0,k=0;
while(sum)
{
sum = 0;
for(int i=0;i<len;i++){
d = input[i] / 2;
sum += d;
if(i == (len - 1)){
output[k++] = input[i] % 2;
}
else
input[i+1] += (input[i]%2)*10;
input[i] = d;
}
}
}
LL pow(LL a, int n[], LL p) //快速幂 a^n % p
{
LL ans = 1;
int i=0;
while(i<k)
{
if(n[i] == 1) ans = ans * a % p;
a = a * a % p;
i++;
}
return ans;
}
int main()
{
LL a,b,c;
while(cin>>a>>str>>c)
{
to_bin(str);
cout<<pow(a,output,c)<<endl;
}
}筛选法求素数
const int N= 1e6; // 素数表范围
bool isp[N+5];
int len = 0, p[N+5];
void prime() { //推荐这个,较快
isp[0] = isp[1] = true;
for (int i = 2; i < maxn; i++) {
if(!isp[i]) p[++len] = i;
for (int j = 1; j <= len && p[j]*i < maxn; j++) {
isp[i*p[j]] = true;
if (i%p[j] == 0) break;
}
}
}
void prime() {
for(int i=2; i <= N; i++)
isp[i] = true;
int n = sqrt(N);
for(int i=2; i <= n; i++) if(isp[i]) {
for(int j=2; i*j <= N; j++)
isp[i*j] = false;
}
}求 n!的位数
#include <bits/stdc++.h>
using namespace std;
const double PI = acos(-1.0);
const double e = exp(1.0);
int main() {
int n ;
cin >> n;
//斯特林定理求N!的位数
double res = log10(sqrt(2*PI*n)) + log10(n/e)*n + 1;
cout << res << endl;
// //log求N!的位数
double ans = 1;
for(int i=1;i <= n; i++)
ans += log10((double)i);
cout << ans << endl;
return 0;
}阶乘最后非零位
/*==================================================*\
| 阶乘最后非零位,复杂度O(nlogn)
\*==================================================*/
//返回该位, n以字符串方式传入
#include <string.h>
#define MAXN 10000
const int mod[20]={1,1,2,6,4,2,2,4,2,8,4, 4,8,4,6,8,8,6,8,2};
int lastdigit(char* buf) {
int len=strlen(buf), a[MAXN], i, c, ret=1;
if (len==1) return mod[buf[0]-'0'];
for (i=0;i<len;i++) a[i]=buf[len-1-i]-'0';
for (; len; len-=!a[len-1]){
ret = ret * mod[a[1] % 2*10+a[0]] % 5;
for (c=0,i=len-1; i>=0; i--)
c = c*10+a[i], a[i]=c/5, c%=5;
}
return ret+ret%2*5;
} 欧拉函数
/*---------------------欧拉定理------------------------
欧拉函数: 1~n中和n互素的元素个数φ(n)
Euler定理:若gcd(a, n)=1则a^φ(n)=1 (mod n),
当b很大时a^b =a^(b modφ(n))(mod n)
对于质数p, φ(p) = p-1, φ(p^n) = p^(n-1)* φ(p);
当(m,n)=1时,φ(mn)=φ(m)*φ(n)。
-----------------------------------------------------*/
/*==================================================*\
|递推求欧拉函数phi(i)
\*==================================================*/
for (i = 1; i <= maxn; i++) phi[i] = i;
for (i = 2; i <= maxn; i += 2) phi[i] /= 2;
for (i = 3; i <= maxn; i += 2) if(phi[i] == i) {
for (j = i; j <= maxn; j += i)
phi[j] = phi[j] / i * (i - 1);
}
/*==================================================*\
|单独求欧拉函数phi(x)
\*==================================================*/
unsigned euler(unsigned x)
{// 就是公式
unsigned i, res=x;
for (i = 2; i < (int)sqrt(x * 1.0) + 1; i++)
if(x%i==0) {
res = res / i * (i - 1);
while (x % i == 0) x /= i; // 保证i一定是素数
}
if (x > 1) res = res / x * (x - 1);
return res;
} 最大公约数(GCD)
/*==================================================*\
| GCD 最大公约数
\*==================================================*/
int gcd(int x, int y){
if (!x || !y) return x > y ? x : y;
for (int t; t = x % y; x = y, y = t);
return y;
}
/*==================================================*\
| 快速 GCD
\*==================================================*/
int kgcd(int a, int b){
if (a == 0) return b;
if (b == 0) return a;
if (!(a & 1) && !(b & 1)) return kgcd(a>>1, b>>1) << 1;
else if (!(b & 1)) return kgcd(a, b>>1);
else if (!(a & 1)) return kgcd(a>>1, b);
else return kgcd(abs(a - b), min(a, b));
}
/*==================================================*\
| 扩展 GCD
| 求x, y使得gcd(a, b) = a * x + b * y;
\*==================================================*/
int extgcd(int a, int b, int & x, int & y){
if (b == 0) { x=1; y=0; return a; }
int d = extgcd(b, a % b, x, y);
int t = x; x = y; y = t - a / b * y;
return d;
} 扩展欧几里德算法 extended-gcd
//一定存在整数x,y,使得ax+by=gcd(a,b)。
int extendedgcd (int a, int b, int&x, int& y) {
if(!b) {
x = 1, y = 0;
return a;
}
int r = gcd(b, a%b, x, y);
int t = x;
x = y;
y = t – a/b*y;
return r;
}
int extendedgcd(int a, int b, __int64 &x, __int64 &y) {
if(!b) {
x = 1 , y = 0;
return a;
}
int r = extendedgcd (b, a%b, y, x);
y -= x * ( a / b );
}
组合数学相关
/*==================================================*\
| Polya计数
| c种颜色的珠子, 组成长为s的项链, 项链没有方向和起始位置;
\*==================================================*/
int gcd (int a, int b) { return b ? gcd(b,a%b) : a; }
int main (void){
int c, s;
while (scanf("%d%d", &c, &s)==2) {
int k;
long long p[64]; p[0] = 1; // power of c
for (k=0 ; k<s ; k++) p[k+1] = p[k] * c;
// reflection part
long long count = s&1 ? s * p[s/2 + 1] : (s/2) * (p[s/2] + p[s/2 + 1]);
// rotation part
for (k=1 ; k<=s ; k++) count += p[gcd(k, s)];
count /= 2 * s;
cout << count << '\n';
}
return 0;
}
/*==================================================*\
| 组合数C(n, r)
\*==================================================*/
int com(int n, int r){// return C(n, r)
if( n-r > r ) r = n-r; // C(n, r) = C(n, n-r)
int i, j, s = 1;
for( i=0, j=1; i < r; ++i ) {
s *= (n-i);
for( ; j <= r && s%j == 0; ++j ) s /= j;
}
return s;
}
/*==================================================*\
| O(n) 求组合数 从开始从左到右递推,注意爆int
\*==================================================*/
C[0] = 1;
for(int i = 1; i <= n; i++)
C[i] = C[i - 1] * (n - i + 1) / i;大数平方根
/*==================================================*\
| 大数平方根(字符串数组表示)
\*==================================================*/
void Sqrt(char *str) {
double i, r, n;
int j, l, size, num, x[1000];
size = strlen(str);
if( size == 1 && str[0] == '0' ) {
printf("0\n"); return;
}
if( size%2 == 1 ) {
n = str[0]-48; l = -1;
} else {
n = (str[0]-48)*10+str[1]-48;
l = 0;
}
r = 0; num = 0;
while(true) {
i = 0;
while( i*(i+20*r) <= n ) ++i; --i;
n -= i*(i+20*r);
r = r*10+i;
x[num] = (int)i;
++num;
l += 2;
if( l >= size ) break;
n = n*100+(double)(str[l]-48)*10+(double)(str[l+1]-48);
}
for(j = 0;j < num; j++)
printf("%d", x[j]);
printf("\n");
} 错排公式
// 问题: 十本不同的书放在书架上。现重新摆放,使每本书都不在原来放的位置。有几种摆法?
// 这个问题推广一下,就是错排问题,是组合数学中的问题之一。
// 考虑一个有n个元素的排列,若一个排列中所有的元素都不在自己原来的位置上,
// 那么这样的排列就称为原排列的一个错排。 n个元素的错排数记为D(n)。
// 研究一个排列错排个数的问题,叫做错排问题或称为更列问题。
//dp[i] = (i - 1)*(dp[i - 1] + dp[i - 2]); i > 2
ll a = 0,b = 1,c;
for (int i = 3; i <= n; i++) {
c = ((i - 1) * 1ll * (a + b)) % MOD;
a = b;
b = c;
}
printf("%lld\n",c);指数降幂公式
计算exponial(n):
#include <iostream>
using namespace std;
typedef long long ll;
ll n,m,ans;
ll euler(ll n){ //返回euler(n) ,计算欧拉函数值
ll res=n,a=n;
for(ll i=2;i*i<=a;i++){
if(a%i==0){
res=res/i*(i-1);//先进行除法是为了防止中间数据的溢出
while(a%i==0) a/=i;
}
}
if(a>1) res=res/a*(a-1);
return res;
}
ll fast_mod(ll x,ll n,ll Max) //快速幂
{
ll res=1;
while(n>0)
{
if(n & 1)
res=(res*x)%Max;
x=(x*x)%Max;
n >>= 1;
}
return res;
}
ll func(ll n,ll m){ //循环求解
if(m==1) return 0;
if(n<=5){
ll ans=1;
for(int i=1;i<=n;i++){
ans=fast_mod(i,ans,m);
}
return ans;
}else{
ll phi=euler(m);
ll z=func(n-1,phi);
ans=fast_mod(n,phi+z,m);
}
return ans;
}
void solve(){ //计算exponial(n)
scanf("%lld%lld",&n,&m);
printf("%lld\n",func(n,m));
}
int main(){
solve();
return 0;
}母函数
普通母函数
普通母函数通常解决类似如下的问题: 给5张1元,4张2元,3张5元,要得到15元,有多少种组合? 某些时候会规定至少使用3张1元、1张2元、0张5元。 某些时候会规定有无数张1元、2元、5元
const int MAX=10000;
const int INF=0x3f3f3f3f;
//为计算结果,b为中间结果。
// K对应具体问题中物品的种类数。
//v[i]表示该乘积表达式第i个因子的权重,对应于具体问题的每个物品的价值或者权重。
//n1[i]表示该乘积表达式第i个因子的起始系数,对应于具体问题中的每个物品的最少个数,即最少要取多少个。0
//n2[i]表示该乘积表达式第i个因子的终止系数,对应于具体问题中的每个物品的最多个数,即最多要取多少个。INF
//P为可能出现的最大指数(所求情况)
int a[MAX],b[MAX],P;
int k,v[MAX],n1[MAX],n2[MAX];
//初始化a
void cal(int n) //n为种类数
{
memset(a,0,sizeof(a));
a[0]=1;
for (int i=1;i<=n;i++)//循环每个因子
{
memset(b,0,sizeof(b));
for (int j=n1[i];j<=n2[i]&&j*v[i]<=P;j++)//循环每个因子的每一项
for (int k=0;k+j*v[i]<=P;k++)//循环a的每个项
b[k+j*v[i]]+=a[k];//把结果加到对应位
memcpy(a,b,sizeof(b));//b赋值给a
}
}指数母函数:
用于求多重排列数
如以下问题: 假设有8个元素,其中a1重复3次,a2重复2次,a3重复3次。从中取r个排列,求其排列数。 对于上面的问题“假设有8个元素,其中a1重复3次,a2重复2次,a3重复3次。从中取r个排列,求其排列数。
double c1[N],c2[N];
LL fac[N];
void Fac() //求阶乘
{
fac[0]=1;
for(int i=1;i<=N;i++)
fac[i]=fac[i-1]*i;
}
int a[N]; //1~n每种的个数
void cal(int n,int m) //有n种,取m个
{
memset(c1,0,sizeof(c1));
memset(c2,0,sizeof(c2));
c1[0]=1.0/fac[0];
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
for(int k=0;k+j<=m && k<=a[i];k++)
c2[k+j]+=c1[j]/fac[k];
for(int j=0;j<=m;j++)
c1[j]=c2[j],c2[j]=0;
}
}
ans=c1[m]*fac[m]; //取m个时的多重排列数