2019 GDUT Winter Training V ( 算法优化) 题解

A题

题面：

A - Stars

Astronomers often examine star maps where stars are represented by points on a plane and each star has Cartesian coordinates. Let the level of a star be an amount of the stars that are not higher and not to the right of the given star. Astronomers want to know the distribution of the levels of the stars.

For example, look at the map shown on the figure above. Level of the star number 5 is equal to 3 (it's formed by three stars with a numbers 1, 2 and 4). And the levels of the stars numbered by 2 and 4 are 1. At this map there are only one star of the level 0, two stars of the level 1, one star of the level 2, and one star of the level 3.

You are to write a program that will count the amounts of the stars of each level on a given map.

Input

The first line of the input file contains a number of stars N (1<=N<=15000). The following N lines describe coordinates of stars (two integers X and Y per line separated by a space, 0<=X,Y<=32000). There can be only one star at one point of the plane. Stars are listed in ascending order of Y coordinate. Stars with equal Y coordinates are listed in ascending order of X coordinate.

Output

The output should contain N lines, one number per line. The first line contains amount of stars of the level 0, the second does amount of stars of the level 1 and so on, the last line contains amount of stars of the level N-1.

Sample Input

Sample Output

Hint

This problem has huge input data,use scanf() instead of cin to read data to avoid time limit exceed.

题面描述：

这个题目讲述的是，输入n颗星星的坐标，题目输入这n个坐标是按照y值升序排序，并且如果y值一样的话，那就按照x值从小到大输入，每颗星星的等级等于这颗星星左边和下面存在的星星数量，然后让我们输入等级分别为0,1,2......n-1的星星数目。

题目分析：

这个题目由于n最大为15000，所以两重循环n平方的做法显然不可行，因此我们在求每颗星星左边和下面有多少颗星星的时候需要进行一下优化。当我们在求第i颗星星的等级的时候，很明显前面i-1颗星星的y值小于等于当前第i颗星星的y值，但是我们现在问题是如何求出前面i-1颗星星当中有多少颗星星的x值小于等于当前这颗星星的x值。

这个求解过程可以用树状数组去实现logn的优化，因此时间复杂度便优化成nlogn，对于当前这颗星星，我们可以用树状数组去求前面0到x的星星数目，然后更新x到x的最大值的值，然后用一个数组来记录对应星星等级的星星数目。

最后把这个数组的数输出出来即可。

代码：

#include <iostream>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <stdlib.h>
#include <string>
#include <cstring>
#include <string.h>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#define reg register
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define lowbit(x) (x&(-x))
using namespace std;
const int Maxn=15005;
const int Maxxy=32005;
int cnt[Maxxy],ans[Maxn];
struct Star
{
	int x,y;
};
Star star[Maxn];
int ask(int x)
{
	int ans=0;
	for (;x>0;x-=lowbit(x)) ans+=cnt[x];
	return ans;
}
void updata(int x)
{
	for (;x<=Maxxy;x+=lowbit(x)) cnt[x]++;
}
int main()
{
	int n;
	while (~scanf("%d",&n))
	{
		memset(ans,0,sizeof(ans));
		memset(cnt,0,sizeof(cnt));
		for (reg int i=1;i<=n;i++)
		{
			int x,y;
			scanf("%d%d",&x,&y);
			x++;
			ans[ask(x)]++;
			updata(x);
		}
		for (reg int i=0;i<n;i++) printf("%d\n",ans[i]);
	}
	return 0;
}

B题

题面：

B - A Simple Problem with Integers

You have N integers, A1, A2, ... , AN. You need to deal with two kinds of operations. One type of operation is to add some given number to each number in a given interval. The other is to ask for the sum of numbers in a given interval.

Input

The first line contains two numbers N and Q. 1 ≤ N,Q ≤ 100000.
The second line contains N numbers, the initial values of A1, A2, ... , AN. -1000000000 ≤ Ai ≤ 1000000000.
Each of the next Q lines represents an operation.
"C a b c" means adding c to each of Aa, Aa+1, ... , Ab. -10000 ≤ c ≤ 10000.
"Q a b" means querying the sum of Aa, Aa+1, ... , Ab.

Output

You need to answer all Q commands in order. One answer in a line.

Sample Input

10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4

Sample Output

4
55
9
15

Hint

The sums may exceed the range of 32-bit integers.

题面描述：

题目输入N个数以及Q个操作，操作分为两种，一种是给输入区间内的所有数加上某个数，一种是询问当前某个区间内所有数的总和，题目要求输出询问操作的答案。

题目分析：

这是一道经典的线段树问题，我们首先递归构建一棵树，为了方便求解，我们可以把树的每个节点定义一个结构体记录相应信息，树的根节点记录的区间是1到N，然后二分把1到N这个区间分成两个区间，然后让树的根节点的子节点分别记录这些区间，这样从树的根节点不断向下面的子节点把1到N的区间进行划分，直到区间不能划分为止，证明这个区间左端点等于右端点，那么这个节点所记录区间的总和很明显就是N个数当中的某个数，在当前节点的情况下，如果当前节点的每个子节点都被拓展完后，我们就可以更新这个节点所代表的区间的数值总和，递归完后我们这棵树就记录了很多相应区间的数值总和。

对于更新操作，我们可以从已经建造好的线段树的根节点不断往下拓展，每次拓展到的节点，我们首先先将这个节点所代表区间之前记录加上的数值往下面的节点更新，该节点所记录加上的数值赋值为0，我们都要将这个树的节点所代表的区间与输入区间作比较，如果这个树节点所代表区间与输入区间不存在交集的话，那么返回上一个节点，如果这个树节点所代表的区间是输入区间的子区间的话，那么我在这个树节点先记录下这个树节点所代表区间需要加上的数值，如果这个树节点所代表的区间与输入区间存在交集的话（两个区间没有彼此的包含关系），那么我们可以继续可以从这个节点往下拓展，继续划分区间，因为更新操作会影响到很多树节点所记录的数值发生改变，因此我们需要重新计算这些节点代表区间的数值总和。

对于询问操作，我们可以从已经建造好的线段树的根节点不断往下拓展，每次拓展到的节点，我们首先先将这个节点所代表区间之前记录加上的数值往下面的节点更新，该节点所记录加上的数值赋值为0，我们都要将这个树的节点所代表的区间与输入区间作比较，如果这个树节点所代表区间与输入区间不存在交集的话，那么返回到上一个节点，返回值为0，如果这个树节点所代表的区间是输入区间的子区间的话，那么我们这个节点所记录区间的数值总和，如果这个树节点所代表的区间与输入区间存在交集的话（两个区间没有彼此的包含关系），那么我们可以继续可以从这个节点往下拓展，继续划分区间。最后的函数返回值即为答案。

代码：

#include <iostream>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <stdlib.h>
#include <string>
#include <cstring>
#include <string.h>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#define reg register
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define lowbit(x) (x&(-x))
using namespace std;
const int Maxn=1e5+5;
struct Tree
{
	int left,right;
	ll down,sum;
};
Tree tree[Maxn<<2];
void down(ll root)
{
	if (!tree[root].down) return;
	tree[root<<1].down+=tree[root].down;
	tree[root<<1|1].down+=tree[root].down;
	int mid=(tree[root].left+tree[root].right)>>1;
	tree[root<<1].sum+=tree[root].down*(mid-tree[root].left+1);
	tree[root<<1|1].sum+=tree[root].down*(tree[root].right-mid);
	tree[root].down=0;
}
void buildtree(int root,int left,int right)
{
	tree[root].left=left;tree[root].right=right;
	tree[root].down=0;
	if (left==right)
	{
		scanf("%I64d",&tree[root].sum);
		return;
	}
	int mid=(left+right)>>1;
	buildtree(root<<1,left,mid);
	buildtree(root<<1|1,mid+1,right);
	tree[root].sum=tree[root<<1].sum+tree[root<<1|1].sum;
}
void updata(int root,int left,int right,int val)
{
	if (left>tree[root].right || tree[root].left>right) return;
	if (left<=tree[root].left && tree[root].right<=right)
	{
		tree[root].down+=val;
		tree[root].sum+=(ll)val*(tree[root].right-tree[root].left+1);
		return;
	}
	down(root);
	int mid=(tree[root].left+tree[root].right)>>1;
	updata(root<<1,left,right,val);
	updata(root<<1|1,left,right,val);
	tree[root].sum=tree[root<<1].sum+tree[root<<1|1].sum;
}
ll query(ll root,ll left,ll right)
{
	if (left>tree[root].right || tree[root].left>right) return 0;
	if (left<=tree[root].left && tree[root].right<=right) return tree[root].sum;
	down(root);
	int mid=(tree[root].left+tree[root].right)>>1;
	return query(root<<1,left,right)+query(root<<1|1,left,right);
}
int main()
{
	int N,Q;
	while (~scanf("%d%d",&N,&Q))
	{
		buildtree(1,1,N);
		for (reg int i=1;i<=Q;i++)
		{
			char ch;
			cin>>ch;
			if (ch=='C')
			{
				int x,y,val;
				scanf("%d%d%d",&x,&y,&val);
				updata(1,x,y,val);
				continue;
			}
			int x,y;
			scanf("%d%d",&x,&y);
			printf("%I64d\n",query(1,x,y));
		}
	}
	return 0;
}

C题

题面：

C - Feel Good

Bill is developing a new mathematical theory for human emotions. His recent investigations are dedicated to studying how good or bad days influent people's memories about some period of life.

A new idea Bill has recently developed assigns a non-negative integer value to each day of human life.

Bill calls this value the emotional value of the day. The greater the emotional value is, the better the daywas. Bill suggests that the value of some period of human life is proportional to the sum of the emotional values of the days in the given period, multiplied by the smallest emotional value of the day in it. This schema reflects that good on average period can be greatly spoiled by one very bad day.

Now Bill is planning to investigate his own life and find the period of his life that had the greatest value. Help him to do so.

Input

The first line of the input contains n - the number of days of Bill's life he is planning to investigate(1 <= n <= 100 000). The rest of the file contains n integer numbers a1, a2, ... an ranging from 0 to 10 6 - the emotional values of the days. Numbers are separated by spaces and/or line breaks.

Output

Print the greatest value of some period of Bill's life in the first line. And on the second line print two numbers l and r such that the period from l-th to r-th day of Bill's life(inclusive) has the greatest possible value. If there are multiple periods with the greatest possible value,then print any one of them.

Sample Input

6
3 1 6 4 5 2

Sample Output

60
3 5

题面描述：

题目讲述的是，输入n天的情感值，然后某个时间段的价值等于这个时间段的情感值总和乘以这个时间段内最小情感值的一天的情感值，然后题目让我们求出n天当中所有时间段当中的最大价值，并且输出这个时间段最早是第几天以及最晚是第几天。

题目分析：

这个题目我们一般会想到，假设第i天是我们要枚举的这个时间段最小情感值的一天，根据贪心策略，我们从第i天往左边和往右边去拓展枚举的时间段大小，直到左边和右边找到比第i天情感值小的一天（或者左边和右边已经找到第0天或者第n+1天了），经过这个操作，我们这样枚举出来的时间段显然是第i天情感值作为该时间段中最小情感值一天的情况下的最大区间，在以第i天为枚举时间段情感值最小的一天的前提下，这种情况下时间段的情感值总和乘以第i天情感值是最大的，因此我们只要枚举i从1到n，求出当中的最大值，并且记录这个时间段的最早的一天和最晚的一天即可。

上面的做法很明显需要进行两重循环去求出答案，但是由于n最大可以取1e5，因此时间复杂度很大，出现超时。那么我们需要进行优化的是，我们在枚举第i天的时候，我们可以利用单调栈快速找到以第i天为最小情感值一天的时间段的最早一天是哪一天，我们可以构建一个单调递增的单调栈，当我们枚举到第i天的时候，我们首先先将单调栈的栈顶所代表的第几天的情感值与第i天的进行比较，如果单调栈的栈顶所代表的第几天的情感值大于等于第i天的情感值的话，那么我们就把单调栈栈顶的元素弹出栈顶，继续与新的栈顶元素所代表的第几天的情感值进行比较，如果单调栈为空或者找到了比第i天情感值小的日子的话，那么我们就可以知道当前枚举的时间段的最左边可以拓展到第几天。至于右边的做法，我们可以倒过来循环，同样可以求得以第i天为最小情感值一天的时间段最右边可以拓展到第几天，但是很容易忽略掉的是，我们做完循环后，可能单调栈仍然不是空的，因此我们需要清空单调栈，单调栈里的元素明显前面找不到比它情感值还小的元素或者右边找不到比它情感值还小的元素，因此我们将这些元素的最左边标记为1或者最右边标记为n。

当然，我们其实也没有必要去循环两次来求解，其实用一次循环就可以求出以第i天作为枚举时间段情感值最小的一天的最左边和最右边是第几天，其实我们从第i天往前找前面比第i天情感值小的时候，我们弹出栈的元素的情感值的最右边肯定只能拓展到第i天，因此我们可以顺便更新这些元素的最右边，清空栈的时候也一样，后面的求解与上面的方法一样。

这道题目值得注意的地方是，我们如果找前面某一天的情感值比当前这一天的情感值大的话，那么应该我们枚举的区间应当可以拓展到前面某一天可以拓展到的最左边，这是因为当前这一天的情感值比前面某一天的情感值小，因此当前这一天的情感值肯定比前面某一天能够拓展到最左边的区间内的任何一天情感值都要小。

代码：

#include <iostream>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <stdlib.h>
#include <string>
#include <cstring>
#include <string.h>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#define reg register
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define lowbit(x) (x&(-x))
using namespace std;
const int Maxn=1e5+5;
int l[Maxn],r[Maxn];
ll a[Maxn],sum[Maxn];
stack <int> s;
int main()
{
	int n,T=0;
	while (~scanf("%d",&n))
	{
		if (T) printf("\n");
		T++;
		memset(sum,0,sizeof(sum));
		for (reg int i=1;i<=n;i++)
		{
			scanf("%lld",&a[i]);
			l[i]=r[i]=i;
			sum[i]=sum[i-1]+a[i];
		}
		for (reg int i=1;i<=n;i++)
		{
			if (!s.empty() && a[i]==a[s.top()]) continue;
			while (!s.empty() && a[s.top()]>=a[i])
			{
				r[s.top()]=i-1;
				l[i]=l[s.top()];
				s.pop();
			}
			s.push(i);
		}
		while (!s.empty())
		{
			r[s.top()]=n;
			s.pop();
		}
		ll ans=-1;
		int ansl,ansr;
		for (reg int i=1;i<=n;i++)
		if ((sum[r[i]]-sum[l[i]-1])*a[i]>ans)
		{
			ans=(sum[r[i]]-sum[l[i]-1])*a[i];
			ansl=l[i];ansr=r[i];
		}
		printf("%lld\n",ans);
		printf("%d %d\n",ansl,ansr);
	}
	return 0;
}

D题

题面：

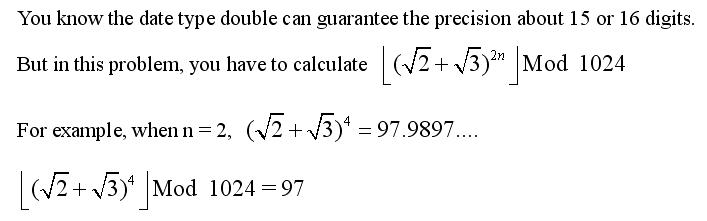
Input

The first line of input gives the number of cases, T. T test cases follow, each on a separate line. Each test case contains one positive integer n. (1 <= n <= 10^9)

Output

For each input case, you should output the answer in one line.

Sample Input

3
1
2
5

Sample Output

9
97
841

题面描述：

这个题目讲述的是，题目输入一个不大于1e9的正整数n，题目要求输出 $\left \lfloor (\sqrt{2}+\sqrt{3})^{2n} \right \rfloor\: Mod\: 1024$ 的值。

题目分析：

这个题目如果我们用一个浮点型变量来存储 $\sqrt{2}+\sqrt{3}$ 的值，然后再用快速幂来求出最终答案的话，答案显然是不对的，因为我们知道浮点型变量存储数据是有范围的，因此最终的答案会存在精度问题。

这个题目给的式子经过推导后，我们可以用矩阵快速幂来求出答案。

$\left \lfloor (\sqrt{2}+\sqrt{3})^{2n} \right \rfloor\: Mod\: 1024=\left \lfloor (5+2*\sqrt{6})^{n} \right \rfloor\: Mod\: 1024$

当n等于1时，我们令 $a_{1}=5,b_{1}=2$ 。

当n等于2时， $a_{2}+b_{2}*\sqrt{6}=(5+2*\sqrt{6})^{2}$

$=(a_{1}+b_{1}*\sqrt{6})*(5+2*\sqrt{6})=(5*a_{1}+12*b_{1})+\sqrt{6}*(2*a_{1}+5*b_{1})$

因此， $a_{2}=5*a_{1}+12*b_{1},b_{2}=2*a_{1}+5*b_{1}$

以此类推， $a_{n}=5*a_{n-1}+12*b_{n-1},b_{n}=2*a_{n-1}+5*b_{n-1}$

因此我们可以将上述表达式用矩阵表示：

$\binom{a_{n}}{b_{n}}=\begin{pmatrix} 5 & 12\\ 2 & 5 \end{pmatrix}\binom{a_{n-1}}{b_{n-1}}$

将上式经过矩阵快速幂后，我们就可以求出 $a_{n}$ 和 $b_{n}$ ，但是我们知道如果将 $\left \lfloor a_{n}+b_{n}*\sqrt{6} \right \rfloor$ 直接输出的话，还是会存在精度问题，因此还要经过一些变化后才能得到精确答案。

经过计算， $(5-2*\sqrt{6})^{n}$ 十分小，可以忽略不计。

$(5+2*\sqrt{6})^{n}\leq (5+2*\sqrt{6})^{n}+(5-2*\sqrt{6})^{n}=a_{n}+b_{n}*\sqrt{6}+a_{n}-b_{n}*\sqrt{6}=2*a_{n}$

因此最终答案为 $2*a_{n}-1$

注意：这上面的计算不要忘了对1024取模

代码：

#include <iostream>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <stdlib.h>
#include <string>
#include <cstring>
#include <string.h>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#define reg register
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define lowbit(x) (x&(-x))
using namespace std;
const int Maxn=1e9+5;
const int mod=1024;
const int N=2;
struct Matrix
{
	int matrix[N][N];
	Matrix ()
	{
		memset(matrix,0,sizeof(matrix));
	}
};
Matrix operator * (const Matrix &a,const Matrix &b)
{
	Matrix temp;
	for (reg int i=0;i<N;i++)
	{
		for (reg int j=0;j<N;j++)
		{
			for (reg int k=0;k<N;k++) temp.matrix[i][j]=(temp.matrix[i][j]+a.matrix[i][k]*b.matrix[k][j])%mod;
		}
	}
	return temp;
}
int ksm(Matrix m,int n)
{
	if (n==1) return 9;
	n--;
	Matrix ans;
	for (reg int i=0;i<N;i++) ans.matrix[i][i]=1;
	while (n)
	{
		if (n&1) ans=ans*m;
		m=m*m;
		n>>=1;
	}
	int s=(ans.matrix[0][0]*5+ans.matrix[0][1]*2)%mod;
	return (2*s-1)%mod;
}
int main()
{
	int T;
	scanf("%d",&T);
	while (T--)
	{
		int n;
		scanf("%d",&n);
		Matrix m;
		m.matrix[0][0]=5;m.matrix[0][1]=12;
		m.matrix[1][0]=2;m.matrix[1][1]=5;
		printf("%d\n",ksm(m,n));
	}
	return 0;
}

E题

题面：

E - Queuing

Queues and Priority Queues are data structures which are known to most computer scientists. The Queue occurs often in our daily life. There are many people lined up at the lunch time.

Now we define that ‘f’ is short for female and ‘m’ is short for male. If the queue’s length is L, then there are 2 L numbers of queues. For example, if L = 2, then they are ff, mm, fm, mf . If there exists a subqueue as fmf or fff, we call it O-queue else it is a E-queue.
Your task is to calculate the number of E-queues mod M with length L by writing a program.

Input

Input a length L (0 <= L <= 10 6) and M.

Output

Output K mod M(1 <= M <= 30) where K is the number of E-queues with length L.

Sample Input

3 8
4 7
4 8

Sample Output

6
2
1

题面描述：

这个题目讲述的是，输入两个变量L和M，问我们长度为L的合法字符串有多少个，最终答案对M取模，所谓的合法字符串即指字符串中不含有fff和fmf这样的子串，字符串中的每一个字符只能是f和m。

题目分析：

当L等于1时，只存在f和m这两种情况，因此答案是2%M。

当L等于2时，只存在ff，fm，mf和mm这四种情况，因此答案为4%M。

对于任意长度为L-1(L>=3)的字符串，我们只需要知道最后两个字符便可以推导出长度为L的合法字符串的数量。

我们可以假设长度为2的字符串，四种后缀(ff,fm,mf,mm)的合法方案全为1。

长度为3的字符串的四种后缀均与长度为2的字符串的四种后缀存在一定的关系：

长度为3且后缀为ff的字符串的合法方案数只能从长度为2且后缀为mf的字符串合法方案数转移过来。

长度为3且后缀为fm的字符串的合法方案数可以从长度为2且后缀为ff和mf的字符串合法方案数转移过来。

长度为3且后缀为mf的字符串的合法方案数只能从长度为2且后缀为mm的字符串合法方案数转移过来。

长度为3且后缀为mm的字符串的合法方案数可以从长度为2且后缀为fm和mm的字符串合法方案数转移过来。

因此长度为3的字符串，四种后缀(ff,fm,mf,mm)的字符串的合法方案分别为：1,2,1,2。

当L大于等于3时，长度为L的合法字符串的四种后缀的方案数均可以像上面一样从长度为L-1的合法字符串的四种后缀的方案数推导出来。

这个题目由于题目给定的n不大于1e6，并且输入数据有多组，所以O(n)的做法显然超时。

因此我们需要用矩阵快速幂来优化，实现O(logn)的做法。

我们分别将上面的四种后缀加上编号，为了简单起见，ff设为0，fm设为1，mf设为2，mm设为3。

根据上面的分析，我们写出递推表达式：

$a[L][0]=a[L-1][2]$

$a[L][1]=a[L-1][0]+a[L-1][2]$

$a[L][2]=a[L-1][3]$

$a[L][3]=a[L-1][1]+a[L-1][3]$

用矩阵表示可以写成：

$\begin{pmatrix} a[L][0]\\ a[L][1]\\ a[L][2]\\ a[L][3] \end{pmatrix}=\begin{pmatrix} 0 & 0 & 1 & 0\\ 1 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & 1 & 0 & 1 \end{pmatrix}\begin{pmatrix} a[L-1][0]\\ a[L-1][1]\\ a[L-1][2]\\ a[L-1][3] \end{pmatrix}$

将上述矩阵表达式进行矩阵快速幂即可求出 $a[L][0]$ , $a[L][1]$ , $a[L][2]$ , $a[L][3]$

上面四者加起来对M取模便为最后答案。

代码：

#include <iostream>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <stdlib.h>
#include <string>
#include <cstring>
#include <string.h>
#include <cmath>
#include <math.h>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#define reg register
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define lowbit(x) (x&(-x))
using namespace std;
const int MaxL=1e6+5;
const int N=4;
int M;
struct Matrix
{
	int matrix[N][N];
	Matrix ()
	{
		memset(matrix,0,sizeof(matrix)); 
	}
};
Matrix operator * (const Matrix &a,const Matrix &b)
{
	Matrix temp;
	for (reg int i=0;i<N;i++)
	{
		for (reg int j=0;j<N;j++)
		{
			for (reg int k=0;k<N;k++) temp.matrix[i][j]=(temp.matrix[i][j]+a.matrix[i][k]*b.matrix[k][j])%M;
		}
	}
	return temp;
}
int ksm(Matrix m,int n)
{
	Matrix ans;
	for (reg int i=0;i<N;i++) ans.matrix[i][i]=1;
	while (n)
	{
		if (n&1) ans=ans*m;
		m=m*m;
		n>>=1;
	}
	int anss=0;
	for (reg int i=0;i<N;i++)
	{
		for (reg int j=0;j<N;j++) anss=(anss+ans.matrix[i][j])%M;
	}
	return anss;
}
int main()
{
	int L;
	while (~scanf("%d%d",&L,&M))
	{
		if (L==1)
		{
			printf("%d\n",2%M);
			continue;
		}
		if (L==2)
		{
			printf("%d\n",4%M);
			continue;
		}
		Matrix m;
		m.matrix[0][0]=m.matrix[0][1]=m.matrix[1][2]=m.matrix[1][3]=m.matrix[2][3]=m.matrix[3][0]=1;
		printf("%d\n",ksm(m,L-2));
	}
	return 0;
}

F题

题面：

F - Expedition

A group of cows grabbed a truck and ventured on an expedition deep into the jungle. Being rather poor drivers, the cows unfortunately managed to run over a rock and puncture the truck's fuel tank. The truck now leaks one unit of fuel every unit of distance it travels.

To repair the truck, the cows need to drive to the nearest town (no more than 1,000,000 units distant) down a long, winding road. On this road, between the town and the current location of the truck, there are N (1 <= N <= 10,000) fuel stops where the cows can stop to acquire additional fuel (1..100 units at each stop).

The jungle is a dangerous place for humans and is especially dangerous for cows. Therefore, the cows want to make the minimum possible number of stops for fuel on the way to the town. Fortunately, the capacity of the fuel tank on their truck is so large that there is effectively no limit to the amount of fuel it can hold. The truck is currently L units away from the town and has P units of fuel (1 <= P <= 1,000,000).

Determine the minimum number of stops needed to reach the town, or if the cows cannot reach the town at all.

Input

* Line 1: A single integer, N

* Lines 2..N+1: Each line contains two space-separated integers describing a fuel stop: The first integer is the distance from the town to the stop; the second is the amount of fuel available at that stop.

* Line N+2: Two space-separated integers, L and P

Output

* Line 1: A single integer giving the minimum number of fuel stops necessary to reach the town. If it is not possible to reach the town, output -1.

Sample Input

4
4 4
5 2
11 5
15 10
25 10

Sample Output

Hint

INPUT DETAILS:

The truck is 25 units away from the town; the truck has 10 units of fuel. Along the road, there are 4 fuel stops at distances 4, 5, 11, and 15 from the town (so these are initially at distances 21, 20, 14, and 10 from the truck). These fuel stops can supply up to 4, 2, 5, and 10 units of fuel, respectively.

OUTPUT DETAILS:

Drive 10 units, stop to acquire 10 more units of fuel, drive 4 more units, stop to acquire 5 more units of fuel, then drive to the town.

题面描述：

题目讲述的是，一群奶牛开着一辆卡车去城镇，但是卡车每行驶一个单位的距离就会泄露一个单位的燃料，由于卡车的燃料有限，现在输入n个加油站，分别输入n个加油站距离城镇的距离以及加油站所拥有的燃料，然后最后一行输入当前卡车距离城镇的距离以及卡车所拥有的燃料，题目让我们求奶牛到达城镇最少需要到达多少个加油站去添加燃料，如果不能到达城镇的话则输出-1。

题目分析：

这个题目让我们求解的是到达城镇最少要经过多少个加油站，根据贪心策略，我们应该尽可能地用光卡车油箱中的燃料，由于燃料有限，因此我们可能不能去到所有的加油站，但是在当前位置至卡车用光所有燃料的位置之间的加油站我们是可以去到的，因此我们先用完当前卡车的燃料，然后再把当前位置至卡车用光所有燃料的位置之间的加油站中最多能够加的燃料加入到优先队列当中，然后优先队列中的数按从大到小排序，然后我们每次卡车用光燃料后，从优先队列中去最大值出来添加燃料，然后再把最大值从优先队列当中删除，并且我们用一个变量去记录我们到达多少个加油站添加燃料，最后判断卡车能不能够到达城镇即可，如果不能够到达的话，那么我们就输出-1，否则输出由原始位置到达城镇最少经过的加油站数量。

代码：

#include <iostream>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <stdlib.h>
#include <string>
#include <cstring>
#include <string.h>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#define reg register
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define lowbit(x) (x&(-x))
using namespace std;
const int Maxn=10005;
struct Stop
{
	int dist,fuel;
};
Stop stop[Maxn];
bool cmp(Stop a,Stop b)
{
	return a.dist>b.dist;
}
int main()
{
	int N;
	while (~scanf("%d",&N))
	{
		for (reg int i=1;i<=N;i++) scanf("%d%d",&stop[i].dist,&stop[i].fuel);
		sort(stop+1,stop+N+1,cmp);
		int L,P;
		scanf("%d%d",&L,&P);
		priority_queue <int> q;
		q.push(P);
		int i=1,ans=0;
		while (L>0 && !q.empty())
		{
			L-=q.top();
			q.pop();
			ans++;
			while (L<=stop[i].dist && i<=N) q.push(stop[i++].fuel);
		}
		if (L<=0) printf("%d\n",ans-1);else printf("-1\n");
	}
	return 0;
}

G题

题面：

G - Sliding Window

An array of size n ≤ 10 6 is given to you. There is a sliding window of size kwhich is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves rightwards by one position. Following is an example:
The array is [1 3 -1 -3 5 3 6 7], and k is 3.

Window position	Minimum value	Maximum value
[1 3 -1] -3 5 3 6 7	-1	3
1 [3 -1 -3] 5 3 6 7	-3	3
1 3 [-1 -3 5] 3 6 7	-3	5
1 3 -1 [-3 5 3] 6 7	-3	5
1 3 -1 -3 [5 3 6] 7	3	6
1 3 -1 -3 5 [3 6 7]	3	7

Your task is to determine the maximum and minimum values in the sliding window at each position.

Input

The input consists of two lines. The first line contains two integers n and k which are the lengths of the array and the sliding window. There are n integers in the second line.

Output

There are two lines in the output. The first line gives the minimum values in the window at each position, from left to right, respectively. The second line gives the maximum values.

Sample Input

8 3
1 3 -1 -3 5 3 6 7

Sample Output

-1 -3 -3 -3 3 3
3 3 5 5 6 7

题面描述：

这个题目讲述的是，输入n个数，问我们在这n个数当中，像1到k，2到k+1，......，n-k+1到n这样的连续序列当中最小的数和最大的数分别是多少。

题目分析：

这个题目是一道经典的单调队列的题目，我们分开两种操作，一种是求n个数中连续k个数当中的最小值，一种是求n个数中连续k个数当中的最大值。

对于求n个数中连续k个数当中的最小值，我们需要维护一个单调递增的单调队列，在这个队列里面，我们必须要保证最后一个元素的下标与第一个元素的下标不能超过k，否则就把第一个元素移出队列。我们初始化队列为空，我们枚举n个数，每次我们把第i个数插入到队列的时候，我们需要判断第i个数是否比队列中最后一个数大，如果第i个数比队列中的最后一个数大的话，那么我们就把第i个数插入到队列的最后面，否则我们就将队列中的最后一个数移出队列，继续找队列中最后一个数与第i个数进行比较，如果队列中所有的数都比第i个数大的话，那么我们就清空队列，然后把第i个数插入到队列，否则把队列所有大于第i个数的数移出队列，然后把第i个数插到队列的最后面。

值得注意的是，我们第一个输出的最小值是当第k个数插入到队列当中后，输出队列的第一个数，以此类推，直到第n个数插入到队列，输出最后一个最小值。

求n个数当中连续k个数当中的最大值的做法也一样，只是我们需要维护的是一个单调递减的单调队列，插入新的数到队列的时候，我们需要将队列当中比这个数小的数全部移出队列，然后再插入到队列，其他操作均相同。

代码：

#include <iostream>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <stdlib.h>
#include <string>
#include <cstring>
#include <string.h>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#define reg register
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define lowbit(x) (x&(-x))
using namespace std;
const int Maxn=1e6+5;
int a[Maxn],window[Maxn];
int main()
{
	int n,k,T=0;
	while (~scanf("%d%d",&n,&k))
	{
		if (T) printf("\n");
		T++;
		for (reg int i=1;i<=n;i++) scanf("%d",&a[i]);
		int head,tail;
		head=1;tail=0;
		for (reg int i=1;i<=n;i++)
		{
			while (i-window[head]+1>k && head<=tail) head++;
			while (head<=tail && a[i]<=a[window[tail]]) tail--;
			window[++tail]=i;
			if (i<k) continue;
			printf("%d",a[window[head]]);
			if (i<n) printf(" ");
		}
		printf("\n");
		head=1;tail=0;
		for (reg int i=1;i<=n;i++)
		{
			while (i-window[head]+1>k && head<=tail) head++;
			while (head<=tail && a[i]>=a[window[tail]]) tail--;
			window[++tail]=i;
			if (i<k) continue;
			printf("%d",a[window[head]]);
			if (i<n) printf(" ");
		}
	}
	return 0;
}

H题

题面：

H - Potted Flower

The little cat takes over the management of a new park. There is a large circular statue in the center of the park, surrounded by N pots of flowers. Each potted flower will be assigned to an integer number (possibly negative) denoting how attractive it is. See the following graph as an example:

(Positions of potted flowers are assigned to index numbers in the range of 1 ... N. The i-th pot and the (i + 1)-th pot are consecutive for any given i (1 <= i < N), and 1st pot is next to N-th pot in addition.)

The board chairman informed the little cat to construct "ONE arc-style cane-chair" for tourists having a rest, and the sum of attractive values of the flowers beside the cane-chair should be as large as possible. You should notice that a cane-chair cannot be a total circle, so the number of flowers beside the cane-chair may be 1, 2, ..., N - 1, but cannot be N. In the above example, if we construct a cane-chair in the position of that red-dashed-arc, we will have the sum of 3+(-2)+1+2=4, which is the largest among all possible constructions.

Unluckily, some booted cats always make trouble for the little cat, by changing some potted flowers to others. The intelligence agency of little cat has caught up all the M instruments of booted cats' action. Each instrument is in the form of "A B", which means changing the A-th potted flowered with a new one whose attractive value equals to B. You have to report the new "maximal sum" after each instruction.

Input

There will be a single test data in the input. You are given an integer N (4 <= N <= 100000) in the first input line.

The second line contains N integers, which are the initial attractive value of each potted flower. The i-th number is for the potted flower on the i-th position.

A single integer M (4 <= M <= 100000) in the third input line, and the following M lines each contains an instruction "A B" in the form described above.

Restriction: All the attractive values are within [-1000, 1000]. We guarantee the maximal sum will be always a positive integer.

Output

For each instruction, output a single line with the maximum sum of attractive values for the optimum cane-chair.

Sample Input

5
3 -2 1 2 -5
4
2 -2
5 -5
2 -4
5 -1

Sample Output

4
4
3
5

题面描述：

这个题目讲述的是，输入n盘花的魅力值，然后输入m个修改操作，每次修改操作更改第i盘花的魅力值，然后每次修改完后输出n盘花当中连续k盘花的最大魅力值的和是多少（1<=k<n）。

题目分析：

这个题目是一道线段树的题目，我们首先先构建一棵线段树，这棵线段树需要记录七个数，分别是这个节点记录区间的数值总和，包括这个区间左端点的最大连续和，包括这个区间左端点的最小连续和，包括这个区间右端点的最大连续和，包括这个区间右端点的最小连续和，这个区间的最大连续和以及这个区间的最小连续和，线段树上的每个叶子节点所记录的以上七个数均是这个区间范围内的花的魅力值。对于这棵树每个节点以上七个数的求法，下面一一详细叙述。

这个节点所记录区间的数值总和等于这个节点所有子节点所记录区间的数值总和的总和。

这个节点包括这个区间左端点的最大连续和等于这个节点的左子节点包括左子节点所记录区间的左端点的最大连续和以及这个节点的左子节点的数值总和加上这个节点的右子节点包括右子节点所记录区间的左端点的最大连续和中的最大值。

这个节点包括这个区间左端点的最小连续和等于这个节点的左子节点包括左子节点所记录区间的左端点的最小连续和以及这个节点的左子节点的数值总和加上这个节点的右子节点包括右子节点所记录区间的左端点的最小连续和中的最小值。

这个节点包括这个区间右端点的最大连续和等于这个节点的右子节点包括右子节点所记录区间的右端点的最大连续和以及这个节点的右子节点的数值总和加上这个节点的左子节点包括左子节点所记录区间的右端点的最大连续和中的最大值。

这个节点包括这个区间右端点的最小连续和等于这个节点的右子节点包括右子节点所记录区间的右端点的最小连续和以及这个节点的右子节点的数值总和加上这个节点的左子节点包括左子节点所记录区间的右端点的最小连续和中的最小值。

这个节点所记录区间的最大连续和等于这个节点的左子节点所记录区间的最大连续和，这个节点的右子节点所记录区间的最大连续和以及这个节点的左子节点所记录区间包括右端点的最大连续和加上这个节点的右子节点所记录区间包括左端点的最大连续和中的最大值。

这个节点所记录区间的最小连续和等于这个节点的左子节点所记录区间的最小连续和，这个节点的右子节点所记录区间的最小连续和以及这个节点的左子节点所记录区间包括右端点的最小连续和加上这个节点的右子节点所记录区间包括左端点的最小连续和中的最小值。

我们每次输入修改需要修改花的编号以及每朵花的魅力值的时候，我们首先递归这棵构建好的线段树，然后找到一个区间仅仅只含这朵花编号，然后这个节点所记录的七个值便改为这朵花变化后的魅力值，然后返回的过程中，修改包含这朵花编号的区间的七个值。

修改操作完成后，我们需要判断1到n的最大连续和是否等于1到n的数值总和，如果是的话，那么我们就输出1到n的数值总和减去1到n的最小连续和（由于题目要求答案不能为1到n的数值总和），否则输出1到n的最大连续和。

代码：

#include <iostream>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <stdlib.h>
#include <string>
#include <cstring>
#include <string.h>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#define reg register
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define lowbit(x) (x&(-x))
using namespace std;
const int Maxn=1e5+5;
const int Maxm=1e5+5;
struct Tree
{
	int left,right;
	int maxf,minf,sum,lmax,rmax,lmin,rmin;
};
Tree tree[Maxn<<2];
void pushup(int root)
{
	tree[root].sum=tree[root<<1].sum+tree[root<<1|1].sum;
	tree[root].maxf=max(max(tree[root<<1].maxf,tree[root<<1|1].maxf),tree[root<<1].rmax+tree[root<<1|1].lmax);
	tree[root].minf=min(min(tree[root<<1].minf,tree[root<<1|1].minf),tree[root<<1].rmin+tree[root<<1|1].lmin);
	tree[root].lmax=max(tree[root<<1].lmax,tree[root<<1].sum+tree[root<<1|1].lmax);
	tree[root].rmax=max(tree[root<<1|1].rmax,tree[root<<1|1].sum+tree[root<<1].rmax);
	tree[root].lmin=min(tree[root<<1].lmin,tree[root<<1].sum+tree[root<<1|1].lmin);
	tree[root].rmin=min(tree[root<<1|1].rmin,tree[root<<1|1].sum+tree[root<<1].rmin);
}
void buildtree(int root,int left,int right)
{
	tree[root].left=left;tree[root].right=right;
	if (left==right)
	{
		scanf("%d",&tree[root].sum);
		tree[root].lmax=tree[root].lmin=tree[root].maxf=tree[root].minf=tree[root].rmax=tree[root].rmin=tree[root].sum;
		return;
	}
	int mid=(left+right)>>1;
	buildtree(root<<1,left,mid);
	buildtree(root<<1|1,mid+1,right);
	pushup(root);
}
void updata(int root,int left,int right,int val)
{
	if (left>tree[root].right || tree[root].left>right) return;
	if (left==tree[root].left && tree[root].right==right)
	{
		tree[root].lmax=tree[root].lmin=tree[root].maxf=tree[root].minf=tree[root].rmax=tree[root].rmin=tree[root].sum=val;
		return;
	}
	updata(root<<1,left,right,val);
	updata(root<<1|1,left,right,val);
	pushup(root);
}
int main()
{
	int N;
	scanf("%d",&N);
	buildtree(1,1,N);
	int M;
	scanf("%d",&M);
	for (reg int i=1;i<=M;i++)
	{
		int A,B;
		scanf("%d%d",&A,&B);
		updata(1,A,A,B);
		if (tree[1].sum==tree[1].maxf)
		{
			printf("%d\n",tree[1].sum-tree[1].minf);
			continue;
		}
		printf("%d\n",max(tree[1].maxf,tree[1].sum-tree[1].minf));
	}
	return 0;
}

I题

题面：

I - Count Color

Chosen Problem Solving and Program design as an optional course, you are required to solve all kinds of problems. Here, we get a new problem.

There is a very long board with length L centimeter, L is a positive integer, so we can evenly divide the board into L segments, and they are labeled by 1, 2, ... L from left to right, each is 1 centimeter long. Now we have to color the board - one segment with only one color. We can do following two operations on the board:

1. "C A B C" Color the board from segment A to segment B with color C.
2. "P A B" Output the number of different colors painted between segment A and segment B (including).

In our daily life, we have very few words to describe a color (red, green, blue, yellow…), so you may assume that the total number of different colors T is very small. To make it simple, we express the names of colors as color 1, color 2, ... color T. At the beginning, the board was painted in color 1. Now the rest of problem is left to your.

Input

First line of input contains L (1 <= L <= 100000), T (1 <= T <= 30) and O (1 <= O <= 100000). Here O denotes the number of operations. Following O lines, each contains "C A B C" or "P A B" (here A, B, C are integers, and A may be larger than B) as an operation defined previously.

Output

Ouput results of the output operation in order, each line contains a number.

Sample Input

2 2 4
C 1 1 2
P 1 2
C 2 2 2
P 1 2

Sample Output

2
1

题面描述：

这个题目讲述的是，有一块长度为L的木板，这块木板被分为L段，这块木板上的每一段原先只有第一种颜色，题目限制了这块木板上的颜色种类不超过T，然后输入O种操作，一种是将某个区间内的每一段木板改为某种颜色，一种是询问我们某个区间内有多少种不同的颜色。

题目分析：

由于这个题目的颜色数量不会超过30种，因此我们可以进行状态压缩，用一个数代表这个区间内含有多少种不同的颜色。

这个题目依然是一道线段树的题目，我们首先初始化这棵线段树的每个节点所记录有多少种颜色不一样的变量为1。

每次我们输入某个需要修改颜色的区间以及需要修改的颜色，我们先将这个区间进行划分，用我们构建好的线段树的节点去表示，然后这些节点的颜色改为需要修改的颜色，然后返回的时候更改上面节点所记录的有多少种颜色不一样的变量，每次访问线段树的节点的时候，我们都需要把之前需要修改这个区间的颜色压到下面的结点。

每次输入询问区间内不一样的颜色有多少种的时候，我们继续将询问区间进行划分，用线段树的节点去表示，然后返回这个节点所记录的有多少种颜色不一样的变量，像上面一样，每个节点被访问的时候把之前需要修改这个区间的颜色压到下面的节点。

最后用一个循环去统计询问出来的数用二进制表示有多少个1即是答案。

代码：

#include <iostream>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <stdlib.h>
#include <string>
#include <cstring>
#include <string.h>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#define reg register
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define lowbit(x) (x&(-x))
using namespace std;
const int MaxL=1e5+5;
struct Tree
{
	int left,right,color,down;
};
Tree tree[MaxL<<2];
void buildtree(int root,int left,int right)
{
	tree[root].left=left;tree[root].right=right;
	tree[root].down=0;
	if (left==right)
	{
		tree[root].color=1;
		return;
	}
	int mid=(left+right)>>1;
	buildtree(root<<1,left,mid);
	buildtree(root<<1|1,mid+1,right); 
	tree[root].color=tree[root<<1].color|tree[root<<1|1].color;
}
void down(int root)
{
	if (!tree[root].down) return;
	tree[root<<1].color=tree[root<<1].down=tree[root].down;
	tree[root<<1|1].color=tree[root<<1|1].down=tree[root].down;
	tree[root].down=0;
}
void updata(int root,int left,int right,int color)
{
	if (left>tree[root].right || tree[root].left>right) return;
	if (left<=tree[root].left && tree[root].right<=right)
	{
		tree[root].color=tree[root].down=1<<(color-1);
		return;
	}
	down(root);
	updata(root<<1,left,right,color);
	updata(root<<1|1,left,right,color);
	tree[root].color=tree[root<<1].color|tree[root<<1|1].color;
}
int query(int root,int left,int right)
{
	if (left>tree[root].right || tree[root].left>right) return 0;
	if (left<=tree[root].left && tree[root].right<=right) return tree[root].color;
	down(root);
	return query(root<<1,left,right)|query(root<<1|1,left,right);
}
int main()
{
	int L,T,O;
	while (~scanf("%d%d%d",&L,&T,&O))
	{
		buildtree(1,1,L);
		for (reg int i=1;i<=O;i++)
		{
			char ch;
			cin>>ch;
			if (ch=='C')
			{
				int A,B,C;
				scanf("%d%d%d",&A,&B,&C);
				if (A>B)
				{
					int temp;
					temp=A;A=B;B=temp;
				}
				updata(1,A,B,C);
				continue;
			}
			int A,B;
			scanf("%d%d",&A,&B);
			if (A>B)
			{
				int temp;
				temp=A;A=B;B=temp;
			}
			int ans=query(1,A,B),cnt=0;
			for (reg int j=0;j<T;j++)
			if (ans&(1<<j)) cnt++;
			printf("%d\n",cnt);
		}
	}
	return 0;
}

J题

题面：

J - Leading and Trailing

You are given two integers: n and k, your task is to find the most significant three digits, and least significant three digits of nk.

Input

Input starts with an integer T (≤ 1000), denoting the number of test cases.

Each case starts with a line containing two integers: n (2 ≤ n < 231) and k (1 ≤ k ≤ 107).

Output

For each case, print the case number and the three leading digits (most significant) and three trailing digits (least significant). You can assume that the input is given such that nk contains at least six digits.

Sample Input

123456 1

123456 2

2 31

2 32

29 8751919

Sample Output

Case 1: 123 456

Case 2: 152 936

Case 3: 214 648

Case 4: 429 296

Case 5: 665 669

题面描述：

这个题目求的是n的k次方的前三位数字和后三位数字是多少。

题目分析：

对于n的k次方的后三位数字的求法，我们可以用快速幂来求出n的k次方，然后每次做乘法运算的时候都要对1000取模，最后答案便为n的k次方的后三位数字。

对于n的k次方的前三位数字的求法，有以下的转化：

$log_{10}(n^{k})=k*log_{10}n$

我们可以发现上面式子的整数部分代表的是这个有多少位，不影响答案，而n的上面式子的小数部分的次方代表的是n的k次方每一位的具体数字是什么，然后乘以100再除去小数部分就是n的k次方的前三位数字。

至于这个题目求10的小数次方可以用pow函数去实现，然后对一个实数取小数部分也可以用fmod函数模1求得。

代码：

#include <iostream>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <stdlib.h>
#include <string>
#include <cstring>
#include <string.h>
#include <cmath>
#include <math.h>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#define reg register
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define lowbit(x) (x&(-x))
using namespace std;
const int mod=1000;
int ksm(int n,int k)
{
	int ans=1;
	n=n%mod;
	while (k)
	{
		if (k&1) ans=(ans*n)%mod;
		n=(n*n)%mod;
		k>>=1;
	}
	return ans;
}
int main()
{
	int T,tt=0;
	scanf("%d",&T);
	while (T--)
	{
		int n,k;
		scanf("%d%d",&n,&k);
		int ans=(int)pow(10.0,2.0+fmod(k*log10(n),1.0));
		printf("Case %d: %d %03d\n",++tt,ans,ksm(n,k));
	}
	return 0;
}

K题

题面：

K - So Easy!

　　A sequence S n is defined as:

Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate S n.
　　You, a top coder, say: So easy!

Input

　　There are several test cases, each test case in one line contains four positive integers: a, b, n, m. Where 0< a, m < 2 15, (a-1) 2< b < a 2, 0 < b, n < 2 31.The input will finish with the end of file.

Output

　　For each the case, output an integer S n.

Sample Input

2 3 1 2013
2 3 2 2013
2 2 1 2013

Sample Output

4
14
4

题面描述：

题目有多组输入，每组输入a，b，n和m，然后让我们求 $\left \lceil (a+\sqrt{b})^{n} \right \rceil\: mod\: m$ 的答案。

题目分析：

这个题目有两种不同构建矩阵的方法。

方法一（与D题类似）：

当n等于1时，直接输出 $\left \lceil (a+\sqrt{b})^{n} \right \rceil$

当n等于2时，假设 $(a+\sqrt{b})^{n}=x_{n}+y_{n}*\sqrt{b}=(x_{n-1}+y_{n-1}*\sqrt{b})*(a+\sqrt{b})$

由上式可以推出， $x_{n}=a*x_{n-1}+b*y_{n-1}$ ， $y_{n}=x_{n-1}+a*y_{n-1}$

用矩阵表达式可以表示为： $\binom{x_{n}}{y_{n}}=\begin{pmatrix} a & b\\ 1 & a \end{pmatrix}\binom{x_{n-1}}{y_{n-1}}$

因此， $\binom{x_{n}}{y_{n}}=\begin{pmatrix} a & b\\ 1 & a \end{pmatrix}^{n-1}\binom{a}{1}$ ，然后用矩阵快速幂把矩阵 $\begin{pmatrix} a & b\\ 1 & a \end{pmatrix}$ 的n-1次方求出来，最后便可求出矩阵 $\binom{x_{n}}{y_{n}}$ 。

由于 $(a-1)^{2}<b<a^{2}$ ，因此 $(a-\sqrt{b})^{n}$ 小于1的，所以我们可以得到 $(a+\sqrt{b})^{n}+(a-\sqrt{b})^{n}=\left \lceil (a+\sqrt{b})^{n} \right \rceil$ 。

$(a-\sqrt{b})^{n}=x_{n}-y_{n}*\sqrt{b}=(x_{n-1}-y_{n-1}*\sqrt{b})*(a-\sqrt{b})$ ，我们会发现 $a+\sqrt{b}$ 和 $a-\sqrt{b}$ 的 $x_{n}$ 和 $y_{n}$ 是一样的。

因此 $\left \lceil (a+\sqrt{b})^{n} \right \rceil=(a+\sqrt{b})^{n}+(a-\sqrt{b})^{n}=x_{n}+y_{n}*\sqrt{b}+x_{n}-y_{n}*\sqrt{b}=2*x_{n}$

方法二（特征根）：

由于 $(a-1)^{2}<b<a^{2}$ ，因此存在结论 $(a+\sqrt{b})^{n}+(a-\sqrt{b})^{n}=\left \lceil (a+\sqrt{b})^{n} \right \rceil$ 。

我们设 $F(n)=(a+\sqrt{b})^{n}+(a-\sqrt{b})^{n}=\left \lceil (a+\sqrt{b})^{n} \right \rceil$

那么我们构造递推关系式： $F(n)=p*F(n-1)+q*F(n-2)$

经过计算，我们可以算出 $p=2*a$ ， $q=b-a*a$ 。

用矩阵表示如下：

$\binom{F(n+1)}{F(n)}=\begin{pmatrix} 2*a & b-a*a\\ 1 & 0 \end{pmatrix}\binom{F(n)}{F(n-1)}$

值得注意的是，n=1时需要特判。

方法三（巧妙推理）：

设 $S_{n}=\left \lceil (a+\sqrt{b})^{n} \right \rceil\: mod\: m$ ， $(a-1)^{2}<b<a^{2}$

记 $A_{n}=(a+\sqrt{b})^{n}$ ， $B_{n}=(a-\sqrt{b})^{n}$ ，

$C_{n}=A_{n}+B_{n}=(a+\sqrt{b})^{n}+(a-\sqrt{b})^{n}$

$A_{n}$ 和 $B_{n}$ 恰好共轭，因此 $C_{n}$ 是整数。

由于 $(a-1)^{2}<b<a^{2}$ ，

$\Rightarrow 0<a-\sqrt{b}<1$

$\Rightarrow 0<(a-\sqrt{b})^{n}<1$

$\Rightarrow 0<B_{n}<1$

因此 $C_{n}=\left \lceil A_{n} \right \rceil$

$S_{n}=(C_{n})\: mod\: m$

对 $C_{n}$ 乘以 $(a+\sqrt{b})+(a-\sqrt{b})$

$C_{n}*(a+\sqrt{b})+(a-\sqrt{b})=[(a+\sqrt{b})^{n}+(a-\sqrt{b})^{n}][(a+\sqrt{b})+(a-\sqrt{b})]$

$=(a+\sqrt{b})^{n+1}+(a-\sqrt{b})^{n+1}+(a+\sqrt{b})^{n}(a-\sqrt{b})+(a-\sqrt{b})^{n}(a+\sqrt{b})$

$=C_{n+1}+(a+\sqrt{b})^{n-1}(a^{2}-b)+(a-\sqrt{b})^{n-1}(a^{2}-b)$

$=C_{n+1}+(a^{2}-b)C_{n-1}$

于是 $C_{n+1}=2*a*C_{n}+(a^{2}-b)C_{n-1}$

用矩阵表示： $\binom{F(n+1)}{F(n)}=\begin{pmatrix} 2*a & b-a*a\\ 1 & 0 \end{pmatrix}\binom{F(n)}{F(n-1)}$

与方法二类似，只是推理方法不同。

值得注意的是，n=1时需要特判。

代码：

方法一：

#include <iostream>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <stdlib.h>
#include <string>
#include <cstring>
#include <string.h>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#define reg register
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define lowbit(x) (x&(-x))
using namespace std;
const int N=2;
int a,b,n,mod;
struct Matrix
{
	ll matrix[N][N];
	Matrix ()
	{
		memset(matrix,0,sizeof(matrix));
	}
};
Matrix operator * (const Matrix &a,const Matrix &b)
{
	Matrix temp;
	for (reg int i=0;i<N;i++)
	{
		for (reg int j=0;j<N;j++)
		{
			for (reg int k=0;k<N;k++) temp.matrix[i][j]=(temp.matrix[i][j]+a.matrix[i][k]*b.matrix[k][j])%mod;
		}
	}
	return temp;
}
ll ksm(Matrix m,int n)
{
	if (n==1)
	{
		ll temp=ceil(a+sqrt(b));
		return temp%mod;
	}
	n--;
	Matrix ans;
	for (reg int i=0;i<N;i++) ans.matrix[i][i]=1;
	while (n)
	{
		if (n&1) ans=ans*m;
		m=m*m;
		n>>=1;
	}
	ll t=(ans.matrix[0][0]*a+ans.matrix[0][1])%mod;
	return (t+t)%mod;
}
int main()
{
	while (~scanf("%d%d%d%d",&a,&b,&n,&mod))
	{
		Matrix m;
		a=a%mod;b=b%mod;
		m.matrix[0][0]=a;m.matrix[0][1]=b;
		m.matrix[1][0]=1;m.matrix[1][1]=a;
		printf("%lld\n",ksm(m,n));
	}
	return 0;
}

方法二（方法三）：

#include <iostream>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <stdlib.h>
#include <string>
#include <cstring>
#include <string.h>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#define reg register
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define lowbit(x) (x&(-x))
using namespace std;
const int N=2;
int a,b,n,mod;
struct Matrix
{
	ll matrix[N][N];
	Matrix ()
	{
		memset(matrix,0,sizeof(matrix));
	}
};
Matrix operator * (const Matrix &a,const Matrix &b)
{
	Matrix temp;
	for (reg int i=0;i<N;i++)
	{
		for (reg int j=0;j<N;j++)
		{
			for (reg int k=0;k<N;k++) temp.matrix[i][j]=((temp.matrix[i][j]+a.matrix[i][k]*b.matrix[k][j])%mod+mod)%mod;
		}
	}
	return temp;
}
ll ksm(Matrix m,int n)
{
	if (n==1) return (2*a)%mod;
	n--;
	Matrix ans;
	for (reg int i=0;i<N;i++) ans.matrix[i][i]=1;
	while (n)
	{
		if (n&1) ans=ans*m;
		m=m*m;
		n>>=1;
	}
	return ((ans.matrix[0][0]*2*a+ans.matrix[0][1]*2)%mod+mod)%mod;
}
int main()
{
	while (~scanf("%d%d%d%d",&a,&b,&n,&mod))
	{
		Matrix m;
		m.matrix[0][0]=2*a;m.matrix[0][1]=b-a*a;
		m.matrix[1][0]=1;m.matrix[1][1]=0;
		printf("%lld\n",ksm(m,n));
	}
	return 0;
}

L题

题面：

L - Largest Rectangle in a Histogram

A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

Input

The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1 <= n <= 100000. Then follow n integers h1, ..., hn, where 0 <= hi <= 1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

Output

For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

Sample Input

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

Sample Output

8
4000

题面描述：

题目讲述的是，输入n个矩阵的高度，然后这n个矩阵的宽都为1，然后题目问我们在直方图当中最大的矩形面积是多少。

题目分析：

我们枚举第1个到第n个矩阵，假设第i个矩阵是我们要选的，然后我们用一个变量来记录包含第i个矩阵的最大矩阵面积，最后输出最大值便为答案。根据贪心策略，我们知道包含第i个矩阵的最大矩阵面积就是往左边找到第一个比第i个矩阵高度小的矩阵以及往右边找到第一个比第i个矩阵高度小的矩阵，然后这个开区间的长度乘上第i个矩阵的高度便为包含第i个矩阵的最大矩阵面积。

但是这题如果像以上两重循环去做的话，显然时间复杂度是 $O(n^{2})$ ，因此我们像C题一样用单调栈去优化，快速把第i个矩阵的左边第一个比第i个矩阵高度小的矩阵找出来以及快速把第i个矩阵的右边第一个比第i个矩阵高度小的矩阵找出来，然后从1枚举到n，取包含第i个矩阵的最大矩阵面积的最大值求出来即可。

代码：

#include <iostream>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <stdlib.h>
#include <string>
#include <cstring>
#include <string.h>
#include <cmath>
#include <math.h>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#define reg register
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define lowbit(x) (x&(-x))
using namespace std;
const int Maxn=1e5+5;
ll h[Maxn];
int l[Maxn],r[Maxn];
int main()
{
	int n;
	while (scanf("%d",&n),n!=0)
	{
		for (reg int i=1;i<=n;i++) scanf("%lld",&h[i]);
		stack <int> s;
		for (reg int i=1;i<=n;i++)
		{
			while (!s.empty() && h[s.top()]>h[i])
			{
				r[s.top()]=i-1;
				s.pop();
			}
			s.push(i);
		}
		while (!s.empty())
		{
			r[s.top()]=n;
			s.pop();
		}
		for (reg int i=n;i>=1;i--)
		{
			while (!s.empty() && h[s.top()]>h[i])
			{
				l[s.top()]=i+1;
				s.pop();
			}
			s.push(i);
		}
		while (!s.empty())
		{
			l[s.top()]=1;
			s.pop();
		}
		ll ans=-1;
		for (reg int i=1;i<=n;i++) ans=max(ans,(ll)h[i]*(r[i]-l[i]+1));
		printf("%lld\n",ans);
	}
	return 0;
}