redis源码--跳跃表

同数组相比，链表的插入删除效率是O(1)，但是如果想要在链表中查找某个元素，就糟糕了，复杂度会是O(N)，为了提高查找效率，就有了跳表的概念。所谓跳表，就是可以跳跃的链表，回想二分查找算法，每次的查找都是跳跃性的，这才使得二分法效率这么高，跳表的设计同样也借鉴了二分法的策略，实现跳跃查找，当然，需要跳表中的元素有序

普通的链表每个节点仅仅保存了指向下一个节点的指针，只能移动到下一个相邻节点，也就是跳一步。而跳表为了可以一次跳很多步，保存了很多指针，指向该节点后面的不同节点

在server.h头文件中，可以找到跳表节点的定义和跳表的定义

/* 跳表节点 */
typedef struct zskiplistNode {
    robj *obj;  /* 数据 */
    double score; /* 分数 */
    struct zskiplistNode *backward; //前一个节点指针
    struct zskiplistLevel {
        struct zskiplistNode *forward; //后面某个节点，也就是next指针
        unsigned int span; //跨度
    } level[]; /* 跳表中保存了多个指向下一个节点的指针 */
} zskiplistNode;

跳表实际上也是保存键值对的结构，其中obj保存实际的数据而score用于排序使用，这保证了跳表内部是有序的。此外，level数组记录了多个指向后面节点的指针，同时也记录了两个节点之间的跨度

为了方便，接下来将跳表节点中指向下一个节点的指针称为next指针，而level数组称为next数组

/* 跳表 */
typedef struct zskiplist {
    struct zskiplistNode *header, *tail; //表头表尾
    unsigned long length; /* 跳表中节点个数 */
    int level; //跳表总层数
} zskiplist;

跳表定义中记录了表头表尾，level记录了当前跳表的总层数

下面是跳表的一个例子，可以看到，每个节点都有若干个next指针，通过这些指针，可以直线跳跃移动，而不再是只能移动到相邻节点

跳表操作
1.创建跳表
创建跳表由zslCreate函数实现，函数中需要调用zslCreateNode创建跳表节点，主要就是申请内存，设置初值

//t_zset.c
/**
 * 创建一个跳表节点
 * level : 节点包含的层数，即节点next数组的大小，每一层有一个next指针 
 * score : 该节点的分值，用于使跳表数据有序
 * obj   : 跳表保存的数据
 **/
zskiplistNode *zslCreateNode(int level, double score, robj *obj) {
    /* 申请跳表节点内存 */
    zskiplistNode *zn = zmalloc(sizeof(*zn)+level*sizeof(struct zskiplistLevel));
    /* 设置初值 */
    zn->score = score;
    zn->obj = obj;
    return zn;
}

/* 创建一个跳表 */
zskiplist *zslCreate(void) {
    int j;
    zskiplist *zsl;

    /* 申请跳表内存, 初始总层数为1 */
    zsl = zmalloc(sizeof(*zsl));
    zsl->level = 1;
    zsl->length = 0;
    /* 申请表头节点，默认有32层 */
    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
    /* 对每一层进行初始化 */
    for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
        zsl->header->level[j].forward = NULL;
        zsl->header->level[j].span = 0;
    }
    zsl->header->backward = NULL;
    /* 设置表尾节点 */
    zsl->tail = NULL;
    return zsl;
}

值得注意的是，表头节点是在创建跳表就申请好的，不属于跳表数据的一部分。

2.搜索操作
跳表的多数操作都是基于搜索的，考虑这样一个需求，就是在跳表中查找某个节点，如果该节点不存在，找到它应该插入的位置。虽然Redis中没有实现搜索功能，但是后面会看到，插入删除等函数都是基于搜索的

假设此时跳表结构如下，需要从跳表中查找分值为23的节点

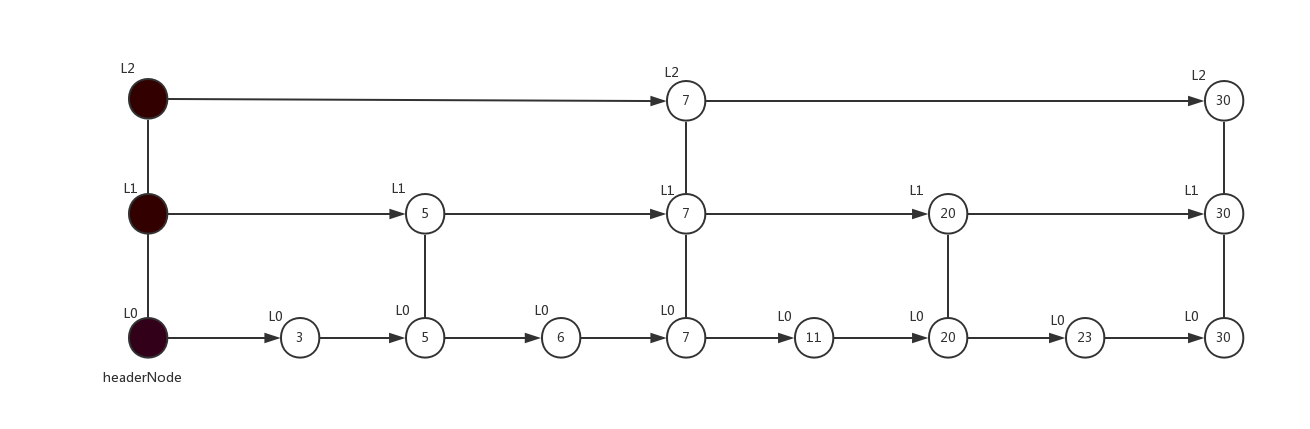
查找操作的步骤如下

从最高层开始尝试移动，比较next节点的分值和待查找分值大小
如果next节点的分值小于待查找分值，则移动到next节点
如果next节点的分值大于等于待查找分值，则降层，如果此时为第0层不能继续降层，当前节点位置就是待查找节点的前一个节点
查找完成后，找到的节点的下一个节点不是待查找节点，就是分值23应该插入的位置

每次搜索操作，不管是找到还是没找到，返回的节点都是目标位置的前一个节点，所以，需要判断返回节点的下一个节点的分值与给定分值的关系从而得知要查找的节点是否在跳表中。当然也可以获得要插入的位置，比如查找分值为21的节点，返回的同样是指向20的节点，该节点的下一个位置就是分值为21应该插入的位置

3.插入操作
插入操作实际上就是执行了一遍搜索功能，由于插入一个节点，会破坏某些节点的next数组。所以需要在搜索过程中记录每一层的前一个节点，以插入22为例，每一层的前一个节点分别是7,20,20三个节点(实际上是两个)

//t_zset.c
/* 在跳表中插入节点，值为score数据为obj */
/* 因为插入节点会破坏原跳表的结构，所以需要先找到会被破坏的那些节点 
 * 被破坏的节点是每一层插入位置的前一个节点，因为它的next数组需要更改 */
zskiplistNode *zslInsert(zskiplist *zsl, double score, robj *obj) {
    /* update保存每一层插入位置的前一个节点 */
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned int rank[ZSKIPLIST_MAXLEVEL];
    int i, level;

    serverAssert(!isnan(score));
    x = zsl->header;
    /* 寻找每一层插入位置的前一个节点 */
    for (i = zsl->level-1; i >= 0; i--) {
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
        /* 实际上就是跳表的查找规则
         * 如果当前层上的next指针指向的节点分值大于要查找的分值，则在同层移动
         * 如果当前层上的next指针指向的节点分值小于要查找的分值，则降层，不移动 */
        /* 而如果要查找每一层插入位置的上一个节点，那么降层时的节点就要要找的节点 */
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                (x->level[i].forward->score == score &&
                compareStringObjects(x->level[i].forward->obj,obj) < 0))) {
            rank[i] += x->level[i].span;
            /* 同层移动 */
            x = x->level[i].forward;
        }
        /* 如果一旦降层，当前节点就是要查找的节点 */
        update[i] = x;
    }
    /* 为新节点随机生成一个层数 */
    level = zslRandomLevel();
    /* 如果随机出的层数大于跳表总层数，那么将跳表扩层 */
    if (level > zsl->level) {
        for (i = zsl->level; i < level; i++) {
            rank[i] = 0;
            update[i] = zsl->header;
            update[i]->level[i].span = zsl->length;
        }
        zsl->level = level;
    }
    /* 创建插入的新节点 */
    x = zslCreateNode(level,score,obj);
    /* 因为新节点只存在[0 : level]层，所以对于高于level层的那些节点没有影响 */
    for (i = 0; i < level; i++) {
        /* 每一层都相当于链表插入 */
        x->level[i].forward = update[i]->level[i].forward;
        update[i]->level[i].forward = x;
        /* 更新跨度span */
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    }
    /* 高层节点的跨度加一 */
    for (i = level; i < zsl->level; i++) {
        update[i]->level[i].span++;
    }

    /* 设置新节点的前一个节点指针 */
    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    /* 如果插入位置是跳表末尾，更新表尾节点 */
    if (x->level[0].forward)
        x->level[0].forward->backward = x;
    else
        zsl->tail = x;
    /* 节点个数增加 */
    zsl->length++;
    return x;
}

4.删除操作
删除操作首先在跳表中查找需要删除的节点，如果找到，则将其删除。需要注意，删除和插入一样，都会破坏某些节点的next指针，所以需要更新

zslDelete函数用于找到匹配的节点，zslDeleteNode函数用于将节点从跳表中删除

//t_zset.c
/* 从跳表中删除节点 */
void zslDeleteNode(zskiplist *zsl, zskiplistNode *x, zskiplistNode **update) {
    int i;
    /* 对于每一层，改变其next数组和跨度 */
    for (i = 0; i < zsl->level; i++) {
        /* 如果当前节点的当前层的next节点是要删除的节点，改变其next指针和跨度 */
        if (update[i]->level[i].forward == x) {
            update[i]->level[i].span += x->level[i].span - 1;
            update[i]->level[i].forward = x->level[i].forward;
        } else {
            /* 否则，只需要改变跨度 */
            update[i]->level[i].span -= 1;
        }
    }
    /* 删除节点后面的后继节点的前驱指针也需要改变 */
    if (x->level[0].forward) {
        x->level[0].forward->backward = x->backward;
    } else {
        zsl->tail = x->backward;
    }
    /* 如果删除的是最高层节点，同时删除后最高层为空，就将跳表层数降低 */
    while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == NULL)
        zsl->level--;
    /* 节点个数减少 */
    zsl->length--;
}

/* 删除分值score和数据obj匹配的节点 */
int zslDelete(zskiplist *zsl, double score, robj *obj) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    int i;

    x = zsl->header;
    /* 寻找待删除节点的前一个节点，和插入操作的查找相同 */
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                (x->level[i].forward->score == score &&
                compareStringObjects(x->level[i].forward->obj,obj) < 0)))
            x = x->level[i].forward;
        update[i] = x;
    }

    /* 判断是否存在要删除的节点，x是插入位置前的节点，那么它的next指针就是需要删除的节点 */
    x = x->level[0].forward;
    if (x && score == x->score && equalStringObjects(x->obj,obj)) {
        /* 如果是，则调用删除节点操作 */
        zslDeleteNode(zsl, x, update);
        zslFreeNode(x);
        return 1;
    }
    return 0; /* not found */
}

5.计算某个节点的排名
Redis跳表可以计算某个数据在跳表中的排名，由zslGetRank函数完成，函数仍然使用查找方法

//t_zset.c
/* 计算数据o在跳表中的排名 */
unsigned long zslGetRank(zskiplist *zsl, double score, robj *o) {
    zskiplistNode *x;
    unsigned long rank = 0;
    int i;

    /* 和插入删除相同的查找操作 */
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                (x->level[i].forward->score == score &&
                compareStringObjects(x->level[i].forward->obj,o) <= 0))) {
            /* 跨度代表当前节点到下一个节点跳过了几个节点，所以排名需要增加跨度个 */
            rank += x->level[i].span;
            x = x->level[i].forward;
        }
        /* 当降层后，说明当前层的下一个节点的值已经大于score了，需要降低一层继续查找
         * 当然也有可能已经找到，所以需要判断是否匹配 */
        if (x->obj && equalStringObjects(x->obj,o)) {
            return rank;
        }
    }
    return 0;
}

对象系统中的跳表
跳表是作为有序集合的底层实现存在的，在object.c文件中，可以看到创建有序集合时将编码设置为跳表

//object.c
/* 创建有序集合对象，底层使用跳表实现 */
robj *createZsetObject(void) {
    /* 申请有序集合内存 */
    zset *zs = zmalloc(sizeof(*zs));
    robj *o;

    /* 为有序集合创建字典 */
    zs->dict = dictCreate(&zsetDictType,NULL);
    /* 创建有序集合中的跳表 */
    zs->zsl = zslCreate();
    o = createObject(OBJ_ZSET,zs);
    /* 设置编码格式为跳表 */
    o->encoding = OBJ_ENCODING_SKIPLIST;
    return o;
}

关于随机算法

一个具有k个后继指针的结点称为k层结点。假设k层结点的数量是k+1层结点的P倍，那么其实这个跳跃表可以看成是一棵平衡的P叉树。跳跃表结点的层数，采用随机化算法得到，实现如下：

int zslRandomLevel(void) {  
    int level = 1;  
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))  
        level += 1;  
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;  
}

这里的ZSKIPLIST_P是0.25。上述代码中，level初始化为1，然后，如果持续满足条件：(random()&0xFFFF)< (ZSKIPLIST_P * 0xFFFF)的话，则level+=1。最终调整level的值，使其小于ZSKIPLIST_MAXLEVEL。

理解该算法的核心，就是要理解满足条件：(random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF)的概率是多少？

random()&0xFFFF形成的数，均匀分布在区间[0,0xFFFF]上，那么这个数小于(ZSKIPLIST_P * 0xFFFF)的概率是多少呢？自然就是ZSKIPLIST_P，也就是0.25了。

因此，最终返回level为1的概率是1-0.25=0.75，返回level为2的概率为0.25*0.75，返回level为3的概率为0.25*0.25*0.75......因此，如果返回level为k的概率为x，则返回level为k+1的概率为0.25*x，换句话说，如果k层的结点数是x，那么k+1层就是0.25*x了。这就是所谓的幂次定律（powerlaw），越大的数出现的概率越小。

测试代码如下：

void test_zslRandomLevel(){  
    unsigned int trytimes = 0xffffff;  
    unsigned int i = 0;  
    int resset[33] = {trytimes,};  
    double percent = 0.0;  
      
    for(i = 0; i < trytimes; i++){  
        resset[zslRandomLevel()]++;  
    }  
      
    for(i = 1; i <= 32; i++){  
        if(resset[i-1] == 0){  
            percent = 0.0;  
        }  
        else{  
            percent = (double)resset[i]/resset[i-1];  
        }     
        printf("resset[%u] is %d, percentage of resset[%u] is %f%%\n",   
            i, resset[i], i-1, percent);  
    }  
}

结果如下：

resset[1] is 12583714, percentage of resset[0] is 0.750048%
resset[2] is 3146005, percentage of resset[1] is 0.250006%
resset[3] is 785421, percentage of resset[2] is 0.249657%
resset[4] is 196516, percentage of resset[3] is 0.250205%
resset[5] is 49350, percentage of resset[4] is 0.251125%
resset[6] is 12163, percentage of resset[5] is 0.246464%
resset[7] is 3024, percentage of resset[6] is 0.248623%
resset[8] is 748, percentage of resset[7] is 0.247354%
resset[9] is 216, percentage of resset[8] is 0.288770%
resset[10] is 46, percentage of resset[9] is 0.212963%
resset[11] is 12, percentage of resset[10] is 0.260870%
resset[12] is 0, percentage of resset[11] is 0.000000%
resset[13] is 0, percentage of resset[12] is 0.000000%
resset[14] is 0, percentage of resset[13] is 0.000000%
resset[15] is 0, percentage of resset[14] is 0.000000%
resset[16] is 0, percentage of resset[15] is 0.000000%
resset[17] is 0, percentage of resset[16] is 0.000000%
resset[18] is 0, percentage of resset[17] is 0.000000%
resset[19] is 0, percentage of resset[18] is 0.000000%
resset[20] is 0, percentage of resset[19] is 0.000000%
resset[21] is 0, percentage of resset[20] is 0.000000%
resset[22] is 0, percentage of resset[21] is 0.000000%
resset[23] is 0, percentage of resset[22] is 0.000000%
resset[24] is 0, percentage of resset[23] is 0.000000%
resset[25] is 0, percentage of resset[24] is 0.000000%
resset[26] is 0, percentage of resset[25] is 0.000000%
resset[27] is 0, percentage of resset[26] is 0.000000%
resset[28] is 0, percentage of resset[27] is 0.000000%
resset[29] is 0, percentage of resset[28] is 0.000000%
resset[30] is 0, percentage of resset[29] is 0.000000%
resset[31] is 0, percentage of resset[30] is 0.000000%
resset[32] is 0, percentage of resset[31] is 0.000000%

可见，层数分布基本上是符合预期的。

猜你喜欢