机器学习面试必知：SVM中解决泛化问题

在前面SVM一文中，我们解得的支持向量机在原始空间中是对训练数据能精确划分的如下图所示。可想而知，有大概率会出现过拟合的问题。这样的支持向量机的泛化能力较差。
因此我们需要一种方式修改支持向量机，允许一些训练数据点被误分类，从而获得一个更好的泛化能力。我们允许数据点在边缘边界的错误侧，同时增加一个惩罚项，这个惩罚项随着与决策边界的距离的增大而增大。我们令这个惩罚项是距离的线性函数，为了实现它我们引入了松弛变量 $\xi_{n}\geq0$，这样每个训练数据点都有一个松弛变量。对于位于正确的边缘边界内部的点或者边界上的点 $\xi_{n}=0$。对于其他的点， $\xi_{n}=|t_{n}-y(x_{n})|$。因此对于位于决策边界 $y(x_{n})=0$上的点， $\xi_{n}=1$,并且 $\xi_{n}>1$就是被误分类的点，所以被精确分类的点满足 $t_{n}y(x_{n})\geq 1-\xi_{n},\quad n=1,...,N$

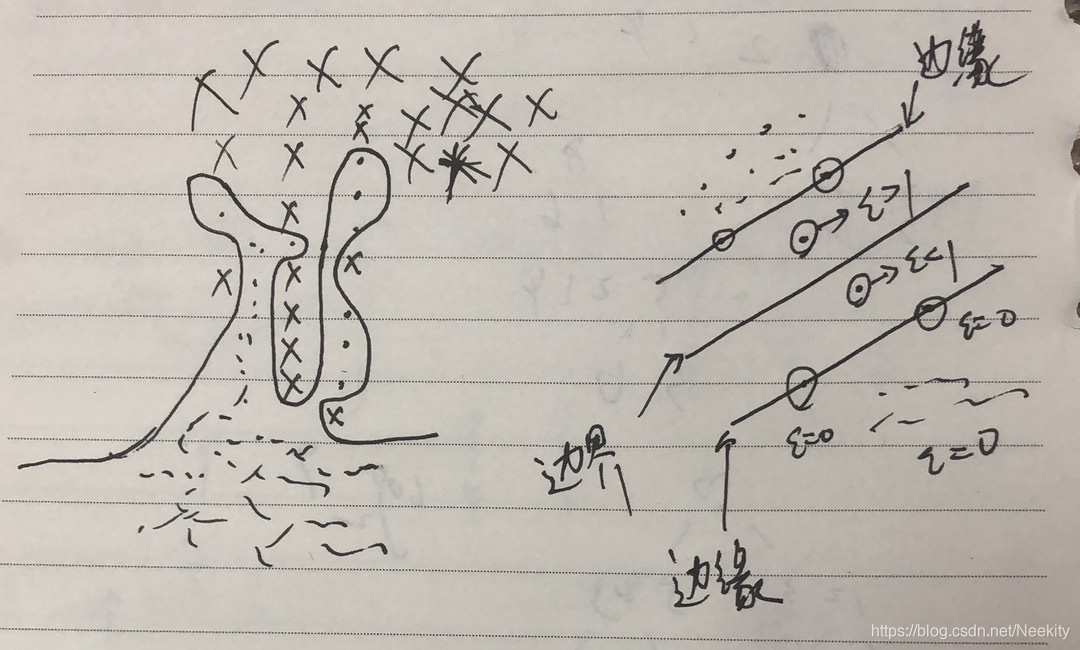
从上图中我们可以看到 $\xi_{n}=0$的数据点被正确分类，要么位于边缘上，要么在边缘正确的一侧。 $0<\xi_{n}<=1$的数据点位于边缘内部，但还是在决策边界的正确一侧。 $\xi_{n}>1$的数据点位于决策边界的错误一侧，是被错误分类的点。

所以这种方法有时被描述成放宽边缘的硬限制，得到一个软边缘，并且能允许一些训练数据点被错分。同时这种方法对异常点很敏感，因为误分类的惩罚随着 $\xi$线性增加。最终我们得到这样一个误差函数 $C\sum_{n=1}^{N}\xi _{n}+\frac{1}{2}||w||^{2}$其中参数 $C\geq0$控制了松弛变量惩罚与边缘之间的折中。由于任何被误分类的数据点都有 $\xi_{n}>1$，因此 $\sum_{n}\xi_{n}$是误分类数据点数量的上界。于是参数C类似于正则化系数，它控制了最小化训练误差与模型复杂度的折中。当C趋向于无穷大时，就是线性可分数据的SVM。与之前的求法类似，我们先写出对应的拉格朗日函数 $L(w,b,\xi,a,u)=\frac{1}{2}||w||^{2}+C\sum_{n=1}^{N}\xi _{n}-\sum_{n=1}^{N}a_{n}\left\{t_{n}y(x_{n})-1+\xi_{n} \right\}-\sum_{n=1}^{N}u_{n}\xi_{n}$对应的KKT条件如下 $a_{n}\geq0$ $t_{n}y(x_{n})-1+\xi_{n}\geq0$ $a_{n}(t_{n}y(x_{n})-1+\xi_{n})=0$ $u_{n}\geq0$ $\xi_{n}\geq0$ $u_{n}\xi_{n}=0$对拉格朗日函数进行最优化 $\frac{\partial L}{\partial w}=0\Rightarrow w=\sum_{n=1}^{N}a_{n}t_{n}\phi(x_{n})$ $\frac{\partial L}{\partial b}=0\Rightarrow 0=\sum_{n=1}^{N}a_{n}t_{n}$ $\frac{\partial L}{\partial \xi}=0\Rightarrow a_{n}=C-u_{n}$把这些结果代入得到 $L(a)=\sum_{n=1}^{N}a_{n}-\frac{1}{2}\sum_{n=1}^{N}\sum_{m=1}^{N}a_{n}a_{m}t_{n}t_{m}K(x_{n},x_{m})$与硬判决相同，但限制条件有差异 $0\leq a_{n}\leq C$ $\sum_{n=1}^{N}a_{n}t_{n}=0$至此我们已经得到了 $w$,接下来求出 $b$，与之前相同考虑KKT条件。我们要找到满足 $\xi_{n}=0$即 $t_{n}y(x_{n})=1$的点 $a_{n}>0,\xi_{n}=0,u_{n}\xi_{n}=0\Rightarrow a_{n}>0,u_{n}>0\Rightarrow a_{n}>0,a_{n}=C-u_{n}<C \Rightarrow 0<a_{n}<C$然后与之前的计算一样 $b=\frac{1}{N_{M}}\sum_{n\in M}\left\{t_{n}-\sum_{m\in S}a_{m}t_{m}K(x_{n},x_{m})\right\}$此时M表示满足 $0<a_{n}<C$的数据点的下标集合