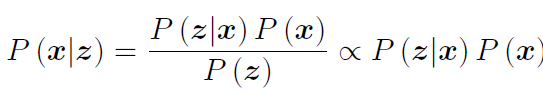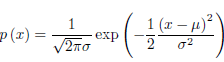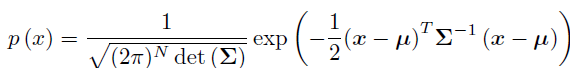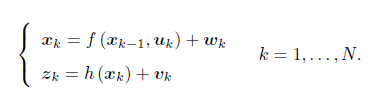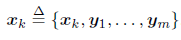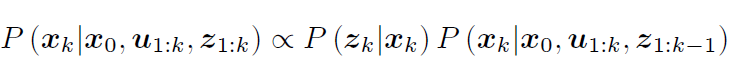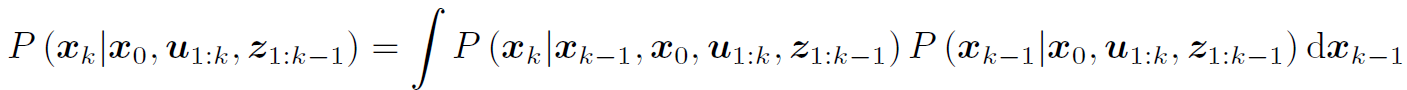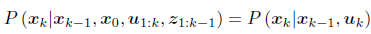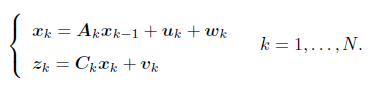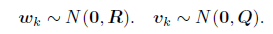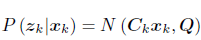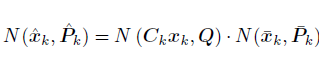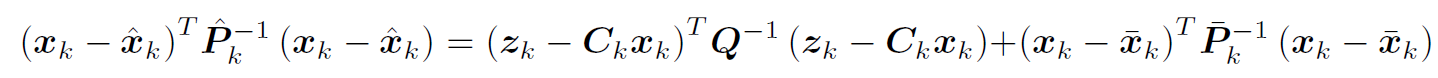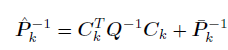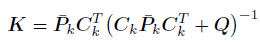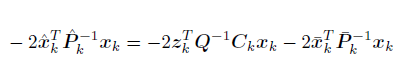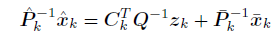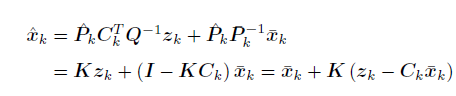什么是卡尔曼滤波
任何含有不确定信息的动态系统中使用卡尔曼滤波,对系统下一步的走向作出有根据的预测,即使伴随着各种扰动,卡尔曼滤波总是能够指出真实发生的情况。
也就是说,通过预测下一步的状态,然后在通过观测值修正自己的估计值。
一、数学基础
1. 贝叶斯公式
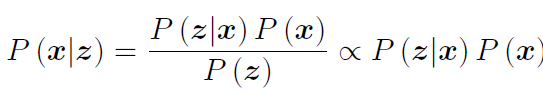
- 公式解释
- P(z)是个定值,不会改变,因此不考虑
- 后验概率P(x|z)
∝ 似然P(z|x)
×先验P(x);
- 为什么使用贝叶斯?
因为后验概率很难求解,所以用贝叶斯公式进行转化;
2. 高斯分布
我们说一个随机变量
x服从高斯分布
N(μ;θ),那么它的概率密度函数为:
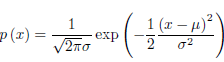
它的高维形式为:
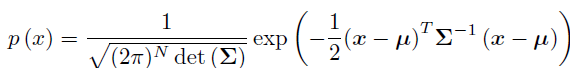
- 两个独立的高斯分布,高斯相加还是高斯;
- 两个独立的高斯分布,高斯相乘还是高斯;
- 复合性质(不是很清楚)
3. 协方差矩阵
协方差矩阵是对称矩阵,
CT=C。
证明:
-
度量各个维度偏离其均值的程度,协方差可以这样来定义:
cov(x,y)=n−1∑i=1n(xi−xˉ)(yi−yˉ)
所以:
cov(x,y)=cov(y,x)
-
举一个三维的例子,假设数据集有三个维度,则协方差矩阵为
C=⎝⎛cov(x,x)cov(y,x)cov(z,x)cov(x,y)cov(y,y)cov(z,y)cov(x,z)cov(y,z)cov(z,z)⎠⎞
所以:
CT=C
二、进入正题
1. 卡尔曼滤波公式全貌

2. 贝叶斯应用于SLAM
- 运动方程和观测方程
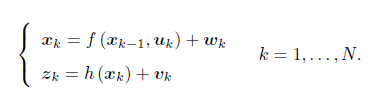
其中
xk含了当前时刻的相机位姿与m 个路标点。
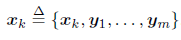
- 用概率来表达
xk的状态分布
P(xk∣x0,u1:k,z1:k)
- 应用贝叶斯法则:后验概率P(x|z)
∝ 似然P(z|x)
×先验P(x);
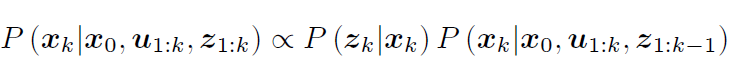
按照
xk−1时刻为条件概率展开,并且假设状态具有马尔科夫性质,当前时刻的状态只与上一时刻相关
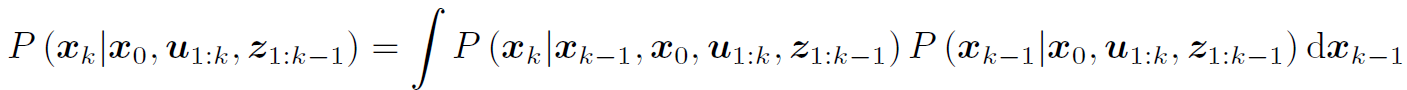
将上述等式的第一部分化简,去掉
x0,u1:k−1,z1:k−1,因为与k-1之前的状态无关(或者说
xk−1状态包含了
x0,u1:k−1,z1:k−1,所以将它们去掉):
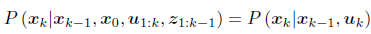
将上述等式的第二部分化简,去掉
uk,因为它与
xk的状态无关:

3. 系统模型
- 运动方程和观测方程可以由线性方程来描述,用最简单的线性高斯系统:
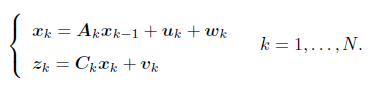
- 假设所有的状态和噪声均满足高斯分布:
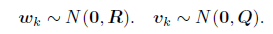
4. 明确目的
已知:
k−1时刻的后验状态估计
x^k−1和它的协方差
P^k−1
输入:k时刻的输入和观测数据
输出:
k时刻的后验状态估计
x^k和它的协方差
P^k
5. 确定先验分布
xkˉ(预测)
符号说明:
- 尖帽子
xk^ 表示后验
- 横线
xˉ 表示先验分布
通过运动方程确定
xkˉ的先验分布
P(xk∣x0,u1:k,z1:k−1)=N(Akx^k−1+uk,AkP^k−1AkT+R)=N(xˉk,Pkˉ)
注意:其中使用了高斯分布的复合性质;
所以先验和协方差矩阵为:
xˉk=Akx^k−1+uk,
Pˉk=AkP^k−1AkT+R
6. 确定似然函数
由由观测方程可知
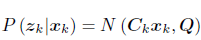
7. 计算后验
公式:后验概率P(x|z)
∝ 似然P(z|x)
×先验P(x);
因为高斯相乘还是高斯,所以后验分布的假设结果为:
xk∼N(k^,P^k)
所以:
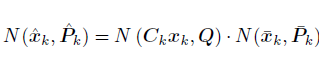
因为两边都是高斯形式,两边的指数相同,展开指数部分可得:
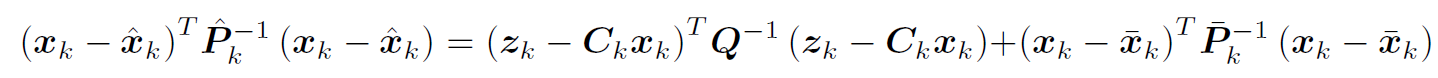
计算协方差
P^k
比较上述公式中两边的
xk的一次和二次系数,可以得到后验分布。
- 其中比较二次系数得到
P^k
- 比较一次系数得到
x^k。
比较二次系数得到
P^k
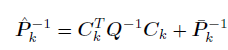
至此,我们达到第一个目的,得到
P^k
但是为了后面的公式推导方便,定义卡尔曼增益K:
K=P^kCkTQ−1
将K代入上面的等式可以得到更简洁的
P^k:
P^k=(I−KCk)Pˉk
计算卡尔曼增益
K
将公式
P^k=(I−KCk)Pˉk代入
K=P^kCkTQ−1消去
K中的
P^k,因为K是一个中间变量,需要用求解出
P^k
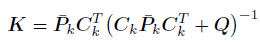
计算
x^k
比较一次系数得到
x^k
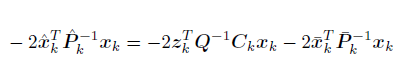
公式中使用了协方差矩阵是对称矩阵的性质。
化简去掉
xk
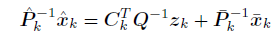
两边同时乘以
P^k,并将
P^k=(I−KCk)Pˉk代入上式:
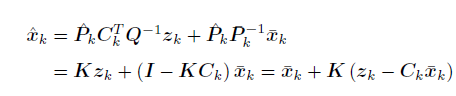
至此,推导完毕。
总结:
本篇博文的卡尔曼滤波推导,参考高翔的《SLAM十四讲》,主要是从概率的角度推导。《概率机器人》一书中也有详细的推导。下面我会附上网上一些大佬写的与卡尔曼滤波相关的博客,很有参考价值。