卡尔曼滤波推导/从一维到多维推导卡尔曼滤波

最近两天在看组合导航相关内容，谈到组合导航，各种滤波技术作为其重要的数据处理方法，值得我们好好学习一番。首先就从卡尔曼滤波（KF）这个比较成熟且应用广泛的技术开始吧。本文从一维简单地例子入手，到多维情况的推导以及卡尔曼滤波如何应用到线性系统中实现状态的最优估计进行简单推导并解释。

为什么

关于卡尔曼滤波的通俗理解，可参考其他博客，有很多有趣的解释，这里主要给出相对正经的回答。
首先，卡尔曼滤波不同于我们平时所接触的各种频域形式的滤波器，比如低通、高通、带通、带阻滤波器等等…相比而言，卡尔曼滤波器是一种时域形式的最优估计，给出对一个变量（状态）的两个不相关的估计，如何对这两个估计进行组合以达到最佳估计（最优估计指标为最小方差）形成一个加权平均是卡尔曼滤波所主要完成的任务。
以导航为例，常用的导航传感器有惯导、GPS、视觉等等…但单独使用某一种传感器都有所不足，且不构成冗余配置。以常用的惯导和GPS为例，惯导系统的优点是：不需要外界提供也不向外辐射任何信息，可工作在任何介质和环境下，且能输出运载体位置、速度、姿态等信息，系统频带宽，输出数据平稳，短期稳定性好等。但其也有明显的缺点，即导航精度随时间而发散，即长期稳定性差。GPS短时间测量精度不如惯导，但GPS不会随时间漂移，输出结果相对稳定，但在密闭环境下会丢失信号，且容易受电磁干扰，失去导航能力。所以常用的导航方法是将该两者结合起来使用，但由于噪声的存在，两者的输出和真值总存在一定的误差，如何对这两组数据加权组合以使输出数据最平稳（方差最小）便是卡尔曼滤波的任务了。

怎么用

知道了为什么要应用卡尔曼滤波，接下来就到了重点：如何进行卡尔曼滤波？为了便于理解，先从一维的例子开始，后推广到 $n$维。（所涉及到的数学基础很少，只需了解一些统计学基本知识即可）

一维下的卡尔曼滤波

所有涉及多维情况下的算法，最简单的最容易理解的办法就是先从一维下手。 $\qquad$ $\qquad$ $\qquad$ $\qquad$ $\qquad$ —我自己

对一个量 $x$的两个不相关估计值 $x_1$、 $x_2$，其相应的方差为 $\sigma_1^2$和 $\sigma_2^2$。要求对这两个估计值进行组合得到加权平均值，即最优或最小方差估计 $\hat x$。通常情况下，这个加权平均值表示如下：
$\hat x_1 = w_1x_1 + w_2x_2 \qquad (1)$ 其中， $w_1$和 $w_2$是加权因子且 $w_1 + w_2 = 1$。 $\hat x$的期望值或均值 $E(\hat x)$表示如下：
$E(\hat x) = w_1E(x_1) + w_2E(x_2) \qquad (2)$ $x$的方差定义为 $E[\{ x - E(x)\}^2 ]$，因此 $\hat x$的方差 $\sigma^2$表示如下：
$\sigma^2 = E\{ ( w_1x_1 + w_2x_2 - w_1E(x_1) - w_2E(x_2) )^2 \} \\ =E\{ w_1^2(x_1-E(x_1))^2 + w_2^2(x_2-E(x_2))^2 \\ - 2w_1w_2(x_1-E(x_1))(x_2-E(x_2)) \} \qquad (3)$由于 $x_1$和 $x_2$互不相关，则 $(x_1-E(x_1))$和 $(x_2-E(x_2))$也互不相关，即 $E\{(x_1-E(x_1))(x_2-E(x_2))\}=0$。因而 $\sigma^2$可表示为：
$\sigma^2=w_1^2E\{ (x_1-E(x_1))^2 \} + w_2^2E\{ (x_2-E(x_2))^2 \} \\=w_1^2\sigma_1^2+w_2^2\sigma_2^2 \qquad (4)$令 $w_2=w$， $w_1=1-w$，方差 $\sigma^2$可表示为：
$\sigma^2=(1-w)^2\sigma_1^2+w^2\sigma_2^2 \qquad (5)$使 $\sigma^2$取得最小的 $w$值，可通过公式(5)对 $w$求微分得到：
$\frac{d\sigma^2}{dw} = -2(1-w)\sigma_1^2+2w\sigma_2^2=0$由上式可求得最优的加权因子：
$w= \frac{\sigma_1^2}{\sigma_1^2+\sigma_2^2} \qquad (6)$将式（6）代入式（1）、式（5），可得到 $\hat x$和它的方差 $\sigma^2$:
$\hat x = \frac{\sigma_2^2x_1+\sigma_1^2x_2}{\sigma_1^2+\sigma_2^2} \qquad(7)$ $\sigma^2= \frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2} \qquad(8)$通过上面的运算，两个不相关的估计值 $x_1$和 $x_2$经过组合得到了加权平均值。加权平均值根据最小方差来选取。在卡尔曼滤波器中，估计值通常通过两种途径获得，其一是根据已知的运动方程，对前一次的最优估计进行更新；另一种途径是从测量值来获取估计值。若把 $x_2$看做测量值，并且用来改善被更新的估计值 $x_1$，则上面的方程可以表示为如下形式：
$\hat x = x_1-w(x_1-x_2) \qquad (9)$ $\sigma^2=\sigma_1^2(1-w) \qquad (10)$这说明了如何利用测量值（ $x_2$）来改善估计值（ $x_1$）和它的方差（ $\sigma_1^2$）。这个过程可以推广到完整卡尔曼滤波的多维形式。

推广到多维卡尔曼滤波

现在，考虑一个 $n$维矢量 $x$，它的两个不相关估计值为 $x_1$和 $x_2$，其方差分别用两个 $n \times n$的矩阵 $P_1$、 $P_2$来表示。
$x_1$和 $x_2$的加权均值可以用如前面讨论的一维情况同样的形式来表示：
$\hat x = (I-W)x_1+Wx_2 = x_1-W(x_1-x_2) \qquad (11)$式中： $W$是一个 $n \times n$阶加权阵； $I$是同阶单位阵； $\hat x$表示 $x$的最优估计。当 $W$的取值使 $\hat x$的方差最小时，可以通过式（11）得到 $x$的最优估计值 $\hat x$。
在许多实际应用中，两个估计值的维数并不相等。例如，用 $y_2$表示 $m$个测量值，而 $y_2$只和 $x$中的某些元素有关，在这种情况下， $y_2$和 $x_2$的关系可以用下式表示：
$y_2=Hx_2 \qquad (12)$式中： $H$是一个 $m\times n$阶矩阵。
因此，可以从估计值 $x_1$（方差为 $P_1$）和估计值 $y_2$（= $H_2x_2$，方差用R表示）得到 $x$的最优估计。令加权矩阵 $W=KH$，式中 $K$是另一任意的加权矩阵，则：
$\hat x=x_1-KH(x_1-x_2)=x_1-K(Hx_1-y_2)\\=(I-KH)x_1+Ky_2 \qquad(13)$由方差的定义可得 $\hat x$的方差 $P$:
$P=E\{ [\hat x -E(\hat x)][\hat x -E(\hat x)]^T \} \qquad (14)$类似地可得到方差 $P_1$和 $R$。把方程（13）代入式（14），可得 $P=E\{ [(I-KH)x_1+Ky_2-(I-KH)E(x_1)\\-KE(Y_2)] - [(I-KH)x_1+Ky_2-(I-KH)E(x_1)\\-KE(Y_2)] ^T \}$由于 $x_1$和 $y_2$不相关，上式可简化为：
$P=(I-KH)E\{ [x_1-E(x_1)][x_1-E(x_1)]^T(I-KH)^T \}\\+KE \{ [y_2-E(y_2)][y_2-E(y_2)]^T \}K^T\\=(I-KH)P_1(I-KH)^T+KRK^T\qquad(15)$现在要寻找能使方差阵 $P$最小的 $K$值，即使 $x$的方差阵 $P$对角线上的元素最小。
参考文献【1】中提供了满足条件的 $K$值：
$K=P_1H^T[HP_1H^T+R]^{-1} \qquad(16)$在这个条件下， $x$的最优估计表示为：
$\hat x = x_1-K[Hx_1-y_2]\qquad(17)$方差表示为：
$P=P_1-KHP_1\qquad(18)$式中， $K$由方程（16）给出。式（16）~（18）定义的加权过程如何应用于卡尔玛女博器，将在下面讨论。

将卡尔曼滤波应用于线性系统

前面所讲的多维情况是假设只有一组估计值来进行最优估计的求解，而对于一个实际运行的系统来说，系统的状态是持续不断到的更新的，这就需要来做一些处理使上面的算法可以持续运行下去，下面我们就来讲解这部分内ring。卡尔曼滤波适用于高斯噪声下的线性系统（若不满足，可考虑其改进算法及其他滤波技术，后面可能会更新这部分）。

线性系统

一个线性系统的动态特性可以用一组一届的微分方程来描述如下：
$\dot x=Fx+Gu+Dw\qquad (19)$式中： $x(t)$为 $n$维系统状态矢量； $u(t)$为 $p$维确定性输入矢量； $w(t)$为系统噪声； $F$是 $n\times n$阶系统矩阵； $G$是 $n\times p$阶系统输入矩阵； $F$、 $G$和 $D$是常值或时变矩阵。系统噪声 $w(t)$均值为零且成高斯分布，功率谱密度为 $Q$。
假设系统有 $m$个测量值，是状态变量 $x(t)$的线性组合，但包含测量噪声。测量值可以用系统状态变量表示如下：
$y=Hx+n \qquad (20)$式中： $y(t)$为 $m$维的测量矢量； $H$是一个 $m\times n$阶的测量矩阵； $n(t)$表示零均值高斯分布的测量噪声，功率谱密度为 $R$。
上述系统用卡尔曼滤波器来求得系统状态变量 $x$的最优估计，已知：

1. 测量值 $y$；
2. 由矩阵 $F$、 $G$、 $H$、 $D$确定的系统模型；
3. 已知系统噪声和测量噪声的统计特性矩阵 $Q$和 $R$。

确定性或可测量的输入通过系统和系统模型来进行处理，如下图所示。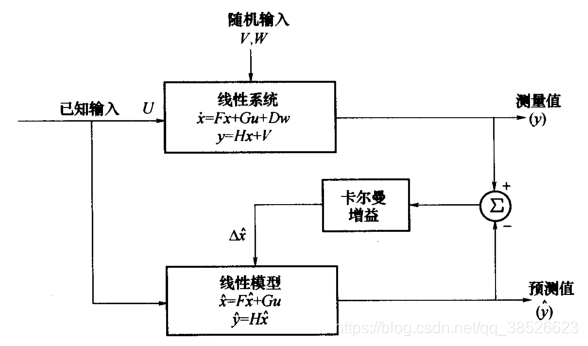
真实系统的测量值和系统的预估值进行比较，系统预估值来自系统模型提供的状态变量的最新最优估计。真值和预估值之间的差异通过一个加权阵，即卡尔曼增益阵，反馈给系统，来校正系统模型的状态估计值。
通常，我们所需的算法为离散形式，故将上述连续方程表示为差分方程形式，如下所示：
$x_{k+1}=\Phi_kx_k+\Gamma_ku_k+\Delta_kw_k\qquad(21)$ $y_{k+1}=H_{k+1}x_{k+1}+n_{k+1}\qquad(22)$式中： $x_k$为 $t_k$时刻的状态矢量； $u_k$为 $t_k$时刻的输入； $w_k$为 $t_k$时刻的系统噪声； $n_{k+1}$为 $t_{k+1}$时刻的测量噪声； $\Phi_k$为 $t_k$至 $t_{k+1}$时刻的状态转移矩阵； $H_{k+1}$为 $t_{k+1}$时刻的测量矩阵； $\Gamma_k$和 $\Delta_k$为适当的输入矩阵。
噪声是离散的零均值噪声，其协方差阵分别为 $Q_k$和 $R_k$。
这些方程用于构成一个递推的卡尔曼滤波算法。在这些公式中，需要考虑两组不同的方程。第一组是基于上一步系统状态最优估计的预测方程，另一组是通过把预测值与新的测量值进行组合，来对预测的最优估计进行更新。

预测更新

在 $t_k$时刻的状态变量 $x_k$的最优估计用 $x_{k/k}$来表示。由于系统具有零均值的白噪声 $w_k$， $t_{k+1}$时刻状态变量的最优预测为：
$x_{k+1/k}=\Phi_kx_{k/k}\qquad(23)$ $t_{k+1}$时刻协方差阵的期望值通过 $t_k$时刻的协方差预测：
$P_{k+1/k}=\Phi_kp_{k/k}\Phi_k^T+\Delta_kQ_k\Delta_k^T\qquad(24)$

扫描二维码关注公众号，回复： 11266595 查看本文章

测量更新

$t_{k+1}$时刻新的测量值 $y_{k+1}$，与来自系统模型的测量值的预测值进行比较，根据上面的算法，用测量值对预测值进行更新，以获得一个最优估计。因此 $t_{k+1}$时刻的状态变量的最优估计如下：
$x_{k+1/k+1}=x_{k+1/k}-K_{k+1}[H_{k+1}x_{k+1/k}-y_{k+1}]\qquad(25)$其协方差为：
$P_{k+1/k+1}=P_{k+1/k}-K_{k+1}H_{k+1}P_{k+1/k}\qquad(26)$式中卡尔曼增益阵为：
$K_{k+1}=P_{k+1/k}H_{k+1}^T[H_{k+1}P_{k+1/k}H_{k+1}^T+R_{k+1}]^{-1}\qquad(27)$这样，每次系统采集到新的测量值，就可利用式（25）~（27）对系统状态进行更新。

注：本文参考国防工业出版社的《捷联惯性导航技术 第二版》，张天光等译。