“测试数据”相当于期中考试，考试的题目和平时课堂上遇到的题目一样，只不过题目中的数据修改了而已，如果考的好，说明自己在课堂上学的东西是真的，可以举一反三应付期末考试了。即通过“测试数据”（期中考试）得到了模型（知识）的泛化性能。

讲到这里，我们不妨把“模型过拟合”的概念也拿出来。通过训练数据（日常课堂上的学习）获得的参数，用于复习（考试的内容和课堂上的一模一样，即训练数据），复习得到95分。接着将训练数据获得的参数用于测试数据，即考试（考试的内容和课堂上的稍有差别）考试只得了50分。可见通过日常的学习而学到的参数模型，只能应付复习，而不能应付考试。说明该同学太死板，知识不能灵活运用，即泛化性能差，模型过拟合，高估了日常的学习能力！

损失函数

既然说神经网络通过学习，获得权重参数，那么它到底是怎么学习的？学习的指标是什么？学到什么程度才算合适？在引入损失函数前，我们打个非常贴切的比方：

有人问你多幸福，你会怎么回答？回答“还可以吧”，“挺幸福的”。这些回答其实都模拟两可，但回答说“我的幸福指数是10.11”，虽然这么回答让人诧异，但是这个答案以数字衡量，比较有参比价值和可比性。如果就以幸福指数为答案规范的话，就很容易比较人们的幸福。

正如以幸福指数这样的指标为指引寻找“最幸福的人一样，神经网络以某个指标为线索寻找最优权重参数。这个指标就是“损失函数”（这只是一种称呼）。不难理解，我们希望幸福指数越大越好，而损失函数的值越小越好。为什么说损失函数的值越小越好，看完下面的知识就知道了。说到这里我们应该可以回答上面的两个问题：学习的指标是损失函数；学到损失函数的值最小或尽量小才算合适。关于神经网络是怎么学习的，看完均方误差和交叉熵误差就知道了。

均方误差

我们说了以“损失函数”这个指标为线索去寻找最优权重参数。因为我们手里只有数据，而机器学习的目的又是通过学习进行推理或预测，显然这些离不开两个条件：一是机器学习，即神经网络的输出；二是数据中正确的标签，这样才能将神经网络的推理与实际值结合起来。是的，神经网络的输出值与输入数据所对应的真实值之间的关系就是我们确定损失函数的切入口。我们直观想到的一种关系是两者之差的平方和。是的，均方误差作为损失函数就诞生了。均方误差E公式如下：

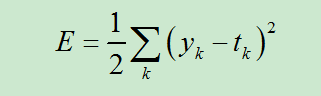
式中， $y_{k}$ 表示神经网络的输出， $t_{k}$ 表示监督数据，k表示数据的维数。比如在神经网络第四篇介绍的手写数字识别的例子中， $y_{k}$ 、 $t_{k}$ 是由如下10个元素构成的数据：

y=[0.1,0.05,0.6,0.0,0.05,0.1,0.0,0.1,0.0,0.0]

t=[0,0,1,0,0,0,0,0,0,0]

数组元素的索引从第1个开始依次对应数字“0”“1”“2”.....“9”。由于softmax函数的输出可以理解为概率，因此“0”的概率是0.1，“1”的概率是0.05，“2”的概率是0.6等。t是监督数据，正确解标签设为1，其他均设为0（这种表示方法称为one-hot）。这里标签“2”为1，表示正确解是“2”。神经网络的输出y的最大值在y[2]取得，即神经网络的输出推理为标签“2”。可见y和t的值计算得到的均方误差E在这种情况下最小（因为神经网络的识别是正确的，如果t的正确解标签不在t[2]处，即神经网络识别错误，这种情况下的E都会变大。）下面我用Python实现并计算。

import numpy as np
def mean_squared_error(y,t):
    return 0.5*np.sum((y-t)**2)
#假设正确解标签为“2”，神经网络输出的“2”的概率最高的情况（0.6）
t=[0,0,1,0,0,0,0,0,0,0]
y=[0.1,0.05,0.6,0.0,0.05,0.1,0.0,0.1,0.0,0.0]
E=mean_squared_error(np.array(y),np.array(t))
print(E)  #输出0.0975，损失函数
#假设正确解标签为“2”，但神经网络的输出的最大值在y[6]处为0.6即识别失败
y=[0.1,0.05,0.1,0.0,0.05,0.1,0.6,0.1,0.0,0.0]
E=mean_squared_error(np.array(y),np.array(t))
print(E)  #输出0.6025，损失函数

从上面的实例可知，当神经网络的输出（识别）正确时，得到的损失函数至为0.0975，当神经网络的输出（识别）错误时，得到的损失函数值为0.6025。可见这样的结论满足上面的叙述：

神经网络的学习，即在损失函数值取得尽可能小的情况下，求得的权重参数，因为这种情况下神经网络的识别更准确。我们不妨假设，神经网络输出的“2”的概率比0.6还大，取0.9，显然神经网络的识别结果更可靠。这种情况下计算得到的损失函数值E也会比0.0975更小。

交叉熵误差

我们先直接给出公式：

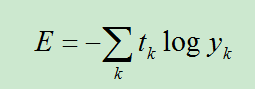
公式中， $y_{k}$ 和 $t_{k}$ 的解释和均方误差公式中的参数解释一样，这里的log表示以e为底数的自然对数。下面我深入解剖该函数：

$\log y_{_{k}}$ ：计算神经网络的各输出值，由于 $y_{k}$ 是softmax函数的输出，所以 $y_{k}$ 的值在0-1之间，因此 $\log y_{_{k}}$ 的值要小于0
$t_{k}$ ：采用one-hot表示，因此 $t_{k}$ 中只有正确解标签的索引为1，其他均为0。
$t_{k}$ $\log y_{_{k}}$ ：分析可知，它们的乘积其实只计算了对应正确解标签的输出的自然对数，其他非正确解标签时 $t_{k}$ 为0，所以乘积也为0。
$-\sum_{k=0}^{k}t_{k}\log y_{k}$ ：由上面的分析可知，在求和符号前添加负号就使得E的值要大于0。

小提示：

log(x)曲线，Python绘制如下：
import numpy as np
import matplotlib.pyplot as plt
x=np.arange(0,1,0.1)
y=np.log(x)
plt.plot(x,y)
plt.show()

假设正确解标签的索引是“2”，与之对应的神经网络的输出是0.6，则交叉熵误差是 $-\log 0.6=0.51$ ，若“2”对应的输出是0.1，则交叉熵误差为 $-\log 0.1=2.30$ 。也就是说正确解标签对应的概率越大，则交叉熵误差（损失函数）的值就越小。这可以结合log(x)函数分析。因此，交叉熵误差的值是由正确解标签所对应的输出结果决定的。

import numpy as np
t=[0,0,1,0,0,0,0,0,0,0]
y=[0.1,0.05,0.6,0.0,0.05,0.1,0.0,0.1,0.0,0.0]
def cross_entropy_error(y,t):
    delta=1e-7
    return -np.sum(t*np.log(y+delta))#防止当y=0时，np.log(0)为无穷大而添加一个微小值。
E=cross_entropy_error(np.array(y),np.array(t))
print(E) #输出0.51
y=[0.1,0.05,0.1,0.0,0.05,0.1,0.6,0.1,0.0,0.0]
E=cross_entropy_error(np.array(y),np.array(t))
print(E) #输出2.30

通过上面的分析，均方误差和交叉熵误差都是可以用作损失函数的，合情合理。

疑问解答：为什么要使用损失函数？

上面我们讨论了损失函数，有人会问：“我们的目的是想获得能提高识别精度的参数，那不是应该把识别精度作为指标吗？而为什么要以损失函数作为指标呢？”

首先，根据上面的介绍，我们应该可以肯定损失函数的作用。在这里我们先解释权重参数的寻优过程：在神经网络的学习中，寻找最优参数，要寻找使损失函数的值尽可能小的参数。而为了找到使损失函数的值尽可能小的地方，需要计算参数的导数（梯度），然后以这个导数为指引，逐步更新参数的值。假设一个神经网络中的某个权重参数，对该参数的损失函数求导，可以理解为“如果稍微改变这个权重参数的值，损失函数的值会如何变化”。根据数学知识可以知道，导数就是一个函数的求解问题，如果导数的值为负，通过使该权重参数向正方向改变，可以减小损失函数的值；如果导数的值为正，则通过使该权重参数向负方向改变，可以减小损失函数的值。当导数为0时，无论权重参数如何变化，损失函数的值都不会改变，即权重参数将在此停止更新。

为什么不用识别精度作为指标？因为这样会导致参数在绝大多数地方都会变成0。打个比方，某个神经网络对100张图片中的30张图片识别正确了，此时识别精度为32%。如果以识别精度为指标，即使稍微改变权重参数的值，识别精度也仍将保持在32%。不会出现变化。即微调参数，无法改变识别精度，即使改变，也不会像30.01%这样连续变化，而是变为31%、32%这样不连续的、离散的值（不难理解吧，图片识别是按一张一张识别的，对就对，错就错）。而如果把损失函数作为指标，则损失函数的值是可以表示为连续的值，比如30.0123......，并且当权重参数稍微改变一下，损失函数也会发现连续改变，比如30.0234.....。所以这就是为什么要选择损失函数作为神经网络的学习指标而不是识别精度。

前面讲过神经网络是不可以用阶跃函数作为激活函数的，因为阶跃函数的导数在大部分地方均为0，在这种情况下，即使即使使用损失函数作为指标，参数的微小变化也会被阶跃函数抹杀，导致损失函数的值不会产生任何变化。反关sigmoid函数，它的导数在任何地方都不为0，这对神经网络的学习很重要，因此神经网络选择sigmoid函数作为激活参数，学习才得以正确进行。下面我们就来介绍使权重参数更新的原理：微分

数值微分

所谓数值微分就是用数值方法近似求解函数的导数的过程。前面我们讲过寻找损失函数最小值对应的权重参数。这句话有几个关键词：损失函数、最小值、对应、权重参数

损失函数：简单地，就是上面我们介绍的损失函数，比如均方误差、交叉熵误差，函数里面均只有两个参数， $y_{k}$ 和 $t_{k}$

最小值：不难理解，最小值就是损失函数的最小值，前面在介绍损失函数时谈到了损失函数值变小、更小值等情况

对应：什么意思？其实就是一种依赖关系，比如函数 $y=x^{2}$ ，求y最小时，x的值，哈哈显然，y的最小值是0，这种情况下对应的x的值只能是0。假设我们把该函数视为损失函数，x视为权重参数，则函数最小值（0）对应的权重参数就是x=0。

权重参数：简单地，就是权重（斜率w）和偏置（截距b）。

显然，我们探讨的寻优过程，是损失函数和权重参数之间的函数关系，与输入数据，激活函数等其他参数无关。

导数概念理解

高等数学讲过导数的概念，但是不生动，我们不妨以一个物理问题来介绍导数的概念：

运动员在开始的5分钟内跑了2千米，则次此时的速度为2/5=0.4千米/分。即运动员以1分钟前进0.4千米的速度在跑步。严格将，这个5分钟内跑了2千米，计算的是5分钟内的平均速度。而导数是某个瞬间的变量，不妨把5分钟的时间尽可能缩短，比如前1分钟跑的距离、前1秒钟跑的距离、前1毫秒跑的距离。这样就能获得某个瞬时的变化量。

所以，导数就是表示某个瞬间的变化量，定义如下式：

$\frac{df\left ( x \right )}{dx}=\lim_{h\rightarrow 0}\frac{f\left ( x+h \right )-f\left ( x \right )}{h}$

公式中的 $\frac{df\left ( x \right )}{dx}$ 表示 $f\left ( x \right )$ 关于 $x$ 的导数，即 $f\left ( x \right )$ 相对于 $x$ 的变化程度。该公式表示的导数的含义是， $x$ 的微小变化将导致函数 $f\left ( x \right )$ 的值在多大程度上发生变化。其中，表示微小变化的 $h$ 无限接近0，表示为 $\lim_{h\rightarrow 0}$ 。上式只用于我们方便理解，实际应用中，由于 $h$ 不可能无限接近0，同时为了减小我们在编程设定 $h$ 为微小值而带来的误差，们一般采用差分的方式来求函数的导数，公式如下：

$\frac{df\left ( x \right )}{dx}=\lim_{2h\rightarrow 0}\frac{f\left ( x+h \right )-f\left ( x-h \right )}{2h}$

这样，用Python实现导数的程序如下;

def numerical_diff(f,x):
    h=1e-5 #0.00001
    return (f(x+h)-f(x-h))/(2*h)

虽然代码只有三行，但是我们仍有必要对其进行分析，这里的微小值 $h$ 不能设定的太小，因为太小会因计算机处理位数带来额外的误差，由于我们采用了差分求导方法，所以 $h$ 可以适当设置大些。函数取名为numerical_diff（）是根据求导的基本原理来的，numerical是数值的意思，differentiation是差分的简写的意思。里面的参数f是函数，可以是上面介绍的损失函数，而参数x可以是神经网络的权重参数。

数值微分在Python中的实现

下面我们利用数值微分的方法来对一个2次函数进行求导，并以绘图的方式表现出来。函数如下：

$y=0.01x^{2}+0.1x$

该函数用Python实现如下：

def function(x):
    return 0.01*x**2+0.1*x

图形的绘制如下：

def function(x):
    return 0.01*x**2+0.1*x
import numpy as np
import matplotlib.pyplot as plt
x=np.arange(0.0,20.0,0.1) #以0.1为步伐，0到20的数组
y=function(x)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.plot(x,y)
plt.show()

接下来，计算一下函数在 $x=5$ 和 $x=10$ 处的导数。

value1=numerical_diff(function,5)
value2=numerical_diff(function,10)
print(value1)  #0.19999999999464887
print(value2)  #0.29999999997532

由程序计算得到的 $x=5$ 和 $x=10$ 处的导数分别为0.1999999和0.29999999。而 $y=0.01x^{2}+0.1x$ 解析性求导结果为 $\frac{df\left ( x \right )}{dx}=0.2x+0.1$ 。因此在 $x=5$ 和 $x=10$ 处的“真的导数”分别为0.2和0.3。这和上面程序计算得到的结果相比，误差几乎可以忽略不计。

偏导数

一般情况下，偏导数是针对一个有多个变量的函数，偏导数和单变量的导数一样，都是求某个地方的斜率。不过，偏导数需要将多个变量中的某一个变量定为目标变量，并将其他变量固定为某个值。比如有一个两个变量的函数如下;

$f\left ( x_{_{0}},x_{_{1}} \right )=x_{_{0}}^{^{2}}+x_{_{1}}^{^{2}}$

该函数可以用python实现，代码如下：

def function1(x0,x1):
    return x0**2+x1**2
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Grab some test data.
x0=np.arange(-3,3,0.1)
x1=np.arange(-3,3,0.1)
x0, x1= np.meshgrid(x0, x1)
y=function1(x0,x1)
# Plot a basic wireframe.
ax.plot_wireframe(x0, x1,y,rstride=5, cstride=5)
ax.set_xlabel('x0')
ax.set_ylabel('x1')
ax.set_zlabel('f(x0,x1)')
plt.show()

$f\left ( x_{_{0}},x_{_{1}} \right )$ 对 $x_{0}$ 和 $x_{1}$ 的求导一般称为偏导数（多个变量），用数学式表示的话，可以写成 $\frac{\partial f}{\partial x_{0}}$ 、 $\frac{\partial f}{\partial x_{1}}$ 。比如当 $x_{0}=3$ ， $x_{1}=4$ 时，求关于 $x_{0}$ 的偏导数 $\frac{\partial f}{\partial x_{0}}$ 和关于 $x_{1}$ 的偏导数 $\frac{\partial f}{\partial x_{1}}$ 。我们利用解析性求解，得到 $\frac{\partial f}{\partial x_{0}}=2x_{_{0}}=2\cdot 3=6$ ， $\frac{\partial f}{\partial x_{1}}=2x_{_{1}}=2\cdot 4=8$ 。用编程计算的结果如下：

def function_tmp1(x0):
    return x0*x0+4.0*2.0
def function_tmp2(x1):
    return 3.0**2.0+x1*x1
result_3=numerical_diff(function_tmp1,3.0)
result_4=numerical_diff(function_tmp2,4.0)
print(result_3)  #6.000000000128124
print(result_4)  #7.999999999874773

可见，编程计算得到的偏导数和解析性计算得到的结果一致。

梯度

在上面，我们按变量分别计算了 $x_{0}$ 和 $x_{1}$ 的偏导数。这里，我们把由全部变量的偏导数汇总而成的向量称为梯度。比如求 $x_{0}=3$ 和 $x_{1}=4$ 时（ $x_{0}$ ， $x_{1}$ ）的偏导数（ $\frac{\partial f}{\partial x_{0}}$ ， $\frac{\partial f}{\partial x_{1}}$ ）就是梯度。所以，梯度和上面介绍的单变量的数值求导基本没有区别。而梯度的意义可以理解为梯度的指示的方向是各点处的函数值减小最多的方向。唯一的区别只是把单变量的求导结果组合在一起。因此在程序上设计稍有变化。代码如下：

import numpy as np
def function_2(x):
    return x[0]**2+x[1]**2  #重新实现上面的示例函数
def numerical_gradient(f,x):
    h=1e-4 #0.0001
    grad=np.zeros_like(x) #生成和x形状相同的数组
    for idx in range(x.size):
        tmp_val=x[idx]
        #f(x+h)的计算
        x[idx]=tmp_val+h
        f1=f(x)
        #f(x-h)的计算
        x[idx]=tmp_val-h
        f2=f(x)
        
        grad[idx]=(f1-f2)/(2*h)
        x[idx]=tmp_val #值还原
    return grad
result=numerical_gradient(function_2,np.array([3.0,4.0]))  #测试
print(result) #输出array([6., 8.])

纵观代码，我们需要解释几点：

1）对函数 $f\left ( x_{_{0}},x_{_{1}} \right )=x_{_{0}}^{^{2}}+x_{_{1}}^{^{2}}$ 的实现function_2()和上一节function_1()代码不一样，这里为了方便理解和同一，我们把x的值放在了数组里面，x[0]对应 $x_{0}$ ，x[1]对应 $x_{1}$ 。不难理解，即使有更多的变量函，数function_2()只需稍作修改即可。

2）因为梯度就是把各变量的偏导数的值组合起来，这里我们用了数组grad来保存 $x_{0}$ 和 $x_{1}$ 的偏导数，它的形状和x相同，初始值值均为0。

3）因为梯度就是单个变量的偏导数的组合，所以我们用了for循环，对所有的变量x均进行了求偏导，实现过程和求单变量的数值微分基本没有区别。

4）函数numerical_gradient(f,x)中，参数f为函数，x为用numpy数组存放的函数变量。上面的测试结果和上一节得到的单变量偏导数结果一致[6,8]。没有小数点是因为numpy输出结果时，数值会被修改为易读的形式而已。

梯度法

我们反复讲，机器学习的主要任务就是在学习时寻找最优参数。同样，神经网络的学习也是在寻找最优参数（权重和偏置）。前面讲过最优参数就是当损失函数取得最小值时的参数。高中数学告诉我们，极值或最小值的求解一般在导数为零的位置。实际上，我们是无法知道损失函数在何处取得最小值，所以我们通过巧妙地使用梯度来寻找函数最小值或尽可能小的值的方法就是梯度法。

由于梯度表示的是各点处的函数值减小最多的方向。因此，无法保证梯度所指向的方向就是函数的最小值或真正应该前进的方向。但如果沿着梯度所指向的方向前进，能最大限度地减小函数的值。所以梯度法是可以使用的。在梯度法中，函数的取值从当前位置沿着梯度方向前进一定距离，然后在新的地方重新求梯度，再沿着新梯度方向前进，如此反复，沿着梯度方向前进逐渐减小函数值。通过对梯度法的解释，我们可以得出梯度法的数学表达式如下;

$x_{0}=x_{0}-\eta \frac{\partial f}{\partial x_{0}}$

$x_{1}=x_{1}-\eta \frac{\partial f}{\partial x_{1}}$

公式中的 $\eta$ 表示多大程度上更新参数，在神经网络的学习中，称为学习率，它表示一次学习中，应该学习多少。该公式表示了更新一次的式子，而后的每一次都会按该公式更新变量的值，通过反复执行次步骤，逐渐减少函数值。即使增加了很多变量，也可以通过类似的式子进行更新。学习率的设置也是一个比较有学问的问题，一般选择0.01或0.001。下面用Python来实现梯度下降法，代码如下：

def gradient_descent(f,init_x,lr=0.01,step_num=100):
    x=init_x
    #初始更新100次
    for i in range(step_num):        
        grad=numerical_gradient(f,x) #求梯度
        x-=lr*grad              #梯度法更新参数
    return x                    #更新停止后的参数

代码中，f是最优化的函数，init_x是参数的初始值，lr四学习率，step_num是梯度法更新的次数，numerical_gradient(f,x)会求函数的梯度，用该梯度乘以学习率得到的值进行更新操作。下面我们用梯度法来试图求取函数 $f\left ( x_{_{0}},x_{_{1}} \right )=x_{_{0}}^{^{2}}+x_{_{1}}^{^{2}}$ 的最小值。我们设定函数的初始位置在（-3.0,4.0），看看梯度法更新100次后函数的位置是不是在最小值处（0,0）。

init_x=np.array([-3.0,4.0])
result=gradient_descent(function_2,init_x,lr=0.1,step_num=100)
print(result)  #输出[-6.11110793e-10  8.14814391e-10]

可见，更新100次后，函数的位置在[-6.11110793e-10 8.14814391e-10]，几乎非常接近（0,0）。函数的最小值就是在（0,0）取得0。所以我们算幸运的，梯度法的更新让我们找到了函数值最小值的位置。读者可尝试设置不同的学习率，可能会得到不一样的结论。所以学习率（我们称为超参数）的设置也是一个很重要的问题。

神经网络的梯度

回到正轨，神经网络的梯度求解才是我们的主题，但是，讲到这里，我们已经很明白了。神经网络的梯度就是值损失函数关于权重参数的梯度。即函数f就是特指损失函数L，x就是特指权重参数W。这里假设我们有一个形状为 $2\times 3$ 的权重的神经网络。则梯度就可以用 $\frac{\partial L}{\partial W}$ 表示，如下：

$\LARGE W=\begin{pmatrix} w_{11} & w_{12}& w_{13}\\ w_{21} &w_{22} &w_{23} \end{pmatrix}$

$\LARGE \frac{\partial L}{\partial W}=\begin{pmatrix} \frac{\partial L}{\partial w_{11}} & \frac{\partial L}{\partial w_{12}} & \frac{\partial L}{\partial w_{13}} \\ \\ \frac{\partial L}{\partial w_{21}} &\frac{\partial L}{\partial w_{22}} &\frac{\partial L}{\partial w_{23}} \end{pmatrix}$

简单解释一下， $\frac{\partial L}{\partial W}$ 的元素由各个元素关于 $W$ 的偏导数构成。比如，第1行第1列的元素 $\frac{\partial L}{\partial W_{11}}$ 表示当 $W_{11}$ 稍微变化时，损失函数 $L$ 会发生多大变化。这里，我们以一个简单的神经网络为例，来实现求梯度的代码。

def softmax(a):
    #在本博客前面的专题讲过该激活函数，这里我再给出来
    c=np.max(a)
    exp_a=np.exp(a-c)
    sum_exp_a=np.sum(exp_a)
    y=exp_a/sum_exp_a
    
    return y 
class simpleNet:
    def __init__(self):
        self.W=np.random.randn(2,3) #高斯分布初始化权重
    def predict(self,x):
        return np.dot(x,self.W)  #输入数据和权重乘积
    def loss(self,x,t):
        z=self.predict(x)  #激活函数的输入
        y=softmax(z)    #激活函数的输出
        loss=cross_entropy_error(y,t) #交叉熵误差作为损失函数
        return loss
#测试代码
net=simpleNet()
x=np.array([0.6,0.9]) #输入数据
p=net.predict(x)
print(p)#[ 1.16970346  0.44492711 -0.52038058]
index=np.argmax(p)  #最大值索引0
print(index)
t=np.array([0,0,1]) #正确解标签,可见预测失败
net.loss(x,t)     #损失函数的输出2.202

#-----------------求梯度-------------------------------------------------------
"""由于权重参数是二维数组，因此实现和前面介绍的一维实现方式有所不同，
这样的改动是为了对应多维数组。这里我们对numerical_gradient函数稍作修改。
"""
def numerical_gradient(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)
    
    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        idx = it.multi_index
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x) # f(x+h)
        
        x[idx] = tmp_val - h 
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        
        x[idx] = tmp_val # 还原值
        it.iternext()   
        
    return grad
def f(W):
    return net.loss(x,t)
dW=numerical_gradient(f,net.W)
print(dW)
#输出：
#[[ 0.35950997  0.17415846 -0.53366842]
#[ 0.53926495  0.26123768 -0.80050264]]

由上面的代码可知，神经网络的预测是错误的，最大值的索引为0，并不是正确解标签所对应的位置索引2。此外，通过一次求梯度得到的dW值有正值和负值，比如 $\frac{\partial L}{\partial W_{11}}$ 为正值，说明 $W_{11}$ 下次应该往负方向更新， $\frac{\partial L}{\partial W_{23}}$ 为负值，说明 $W_{23}$ 下次应该往正方向更新。至于更新的程度， $W_{23}$ 比 $W_{11}$ 的贡献大些。我们通过随机初始化得到的权重参数用于神经网络的预测是失败的。但是我们一旦求出神经网络的梯度后，接下来只需根据梯度法，更新权重参数，就一定能获得让神经网络预测正确的权重参数。在下一节“学习算法的实现”环节，我们将实现整个学习过程，尽可能获得最优权重参数。

学习算法的实现

讲到这里，神经网络学习的相关准备都差不多了，神经网络的学习步骤一般分为如下四步骤：

1）从训练数据中随机抽取一部分数据，这部分数据称为mini-batch，我们的目标是减小mini-batch的损失函数值。

2）为了减少mini-batch的损失函数的值，需要计算权重参数的梯度。

3）将权重参数沿梯度方向进行微小更新。

4）重复步骤1、步骤2、步骤3。

这里介绍的mini-batch是随机选择的，所以我们又称为随机梯度下降法（SGD）。下面我用2层神经网络（隐藏层1层）为对象，使用MNIST数据集进行学习。

class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        # 初始化权重
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

    def predict(self, x):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']
    
        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)
        
        return y
        
    # x:输入数据, t:监督数据
    def loss(self, x, t):
        y = self.predict(x)
        
        return cross_entropy_error(y, t)
    
    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        t = np.argmax(t, axis=1)
        
        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy
        
    # x:输入数据, t:监督数据
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)
        
        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
        
        return grads

上面我们把该2层神经网络实现为1个名为TwoLayerNet的类，下面我们就以该类为对象，使用MNIST数据集进行学习。MNIST数据集的下载程序如下，首次下载需要的时间较长。我们把下载数据集的程序放在文件minst.py文件中，具体的程序如下：

# coding: utf-8
#mnist.py文件的程序
try:
    import urllib.request
except ImportError:
    raise ImportError('You should use Python 3.x')
import os.path
import gzip
import pickle
import os
import numpy as np


url_base = 'http://yann.lecun.com/exdb/mnist/'
key_file = {
    'train_img':'train-images-idx3-ubyte.gz',
    'train_label':'train-labels-idx1-ubyte.gz',
    'test_img':'t10k-images-idx3-ubyte.gz',
    'test_label':'t10k-labels-idx1-ubyte.gz'
}

dataset_dir = os.path.dirname(os.path.abspath(__file__))
save_file = dataset_dir + "/mnist.pkl"

train_num = 60000
test_num = 10000
img_dim = (1, 28, 28)
img_size = 784


def _download(file_name):
    file_path = dataset_dir + "/" + file_name
    
    if os.path.exists(file_path):
        return

    print("Downloading " + file_name + " ... ")
    urllib.request.urlretrieve(url_base + file_name, file_path)
    print("Done")
    
def download_mnist():
    for v in key_file.values():
       _download(v)
        
def _load_label(file_name):
    file_path = dataset_dir + "/" + file_name
    
    print("Converting " + file_name + " to NumPy Array ...")
    with gzip.open(file_path, 'rb') as f:
            labels = np.frombuffer(f.read(), np.uint8, offset=8)
    print("Done")
    
    return labels

def _load_img(file_name):
    file_path = dataset_dir + "/" + file_name
    
    print("Converting " + file_name + " to NumPy Array ...")    
    with gzip.open(file_path, 'rb') as f:
            data = np.frombuffer(f.read(), np.uint8, offset=16)
    data = data.reshape(-1, img_size)
    print("Done")
    
    return data
    
def _convert_numpy():
    dataset = {}
    dataset['train_img'] =  _load_img(key_file['train_img'])
    dataset['train_label'] = _load_label(key_file['train_label'])    
    dataset['test_img'] = _load_img(key_file['test_img'])
    dataset['test_label'] = _load_label(key_file['test_label'])
    
    return dataset

def init_mnist():
    download_mnist()
    dataset = _convert_numpy()
    print("Creating pickle file ...")
    with open(save_file, 'wb') as f:
        pickle.dump(dataset, f, -1)
    print("Done!")

def _change_one_hot_label(X):
    T = np.zeros((X.size, 10))
    for idx, row in enumerate(T):
        row[X[idx]] = 1
        
    return T
    

def load_mnist(normalize=True, flatten=True, one_hot_label=False):
    """读入MNIST数据集
    
    Parameters
    ----------
    normalize : 将图像的像素值正规化为0.0~1.0
    one_hot_label : 
        one_hot_label为True的情况下，标签作为one-hot数组返回
        one-hot数组是指[0,0,1,0,0,0,0,0,0,0]这样的数组
    flatten : 是否将图像展开为一维数组
    
    Returns
    -------
    (训练图像, 训练标签), (测试图像, 测试标签)
    """
    if not os.path.exists(save_file):
        init_mnist()
        
    with open(save_file, 'rb') as f:
        dataset = pickle.load(f)
    
    if normalize:
        for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].astype(np.float32)
            dataset[key] /= 255.0
            
    if one_hot_label:
        dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
        dataset['test_label'] = _change_one_hot_label(dataset['test_label'])
    
    if not flatten:
         for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].reshape(-1, 1, 28, 28)

    return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label']) 


if __name__ == '__main__':
    init_mnist()

有了mnist数据集的下载程序，我们就可以实现神经网络的学习，下面是学习过程的程序，我们把学习中的损失函数值的变化过程记录下来并绘图显示。

# coding: utf-8
import sys, os
os.chdir(r'f:\deep-learning with python')    #根据自己的文件位置，指定文件位置
import numpy as np
import matplotlib.pyplot as plt
from mnist import load_mnist
# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

train_loss_list=[]  #保存损失函数值的列表

#超参数设置

iters_num = 5000  # 适当设定循环的次数
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

for i in range(iters_num):
    #获取mini-batch
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    # 计算梯度
    #grad = network.numerical_gradient(x_batch, t_batch)
    grad=network.gradient(x_batch, t_batch)
    # 更新参数
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]
    #记录学习过程
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)
    
# # 绘制图形
x=np.arange(len(train_loss_list))  #横轴取0-损失值的长度
plt.plot(x,train_loss_list)         #纵轴为损失函数值
plt.xlabel("iteration")
plt.ylabel("loss")
plt.show()
max(train_loss_list)  #最大值2.31
min(train_loss_list)  #最小值0.07

更直挂地，我们只查看前1000次梯度更新的损失函数的值，代码和图线如下：

x=np.arange(len(train_loss_list[:1000]))
plt.plot(x,train_loss_list[:1000])
plt.xlabel("iteration")
plt.ylabel("loss")
plt.show()

总体来说，随着梯度的不断更新，损失函数的值是在减小，从最大值2.31减小至最小值0.07 ，说明神经网络的学习是在顺利进行。接下来，我们就通过运用识别精度指标来确认神经网络的学习是否正确。

测试数据对神经网络学习的评价

通过上面的代码实现，我们确认了通过反复学习可以使损失函数的值逐一减小。现在我们就来确认神经网络是否能够正确识别训练数据意外的其他数据，即模型的泛化性能。下面我们就针对测试数据进行预测，直观地观察神经网络的泛化性能。下面直接给出程序及图形结果（程序和神经网络的学习程序差不多）。

epoch是一个单位，一个epoch表示学习中所有训练数据均被使用一次时的更新次数。比如有10000个数据，用大小为100个数据的mini-batch进行学习，只要重复随机梯度下降法100次，理论上所有的训练数据就被“看过”了。这时，100次就是一个epoch

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from mnist import load_mnist #从上面的mnist.py程序中导入load_mnist函数

# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
#TwoLayerNet()在上文中已经给出
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

iters_num = 10000  # 适当设定循环的次数
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    # 计算梯度
    grad = network.numerical_gradient(x_batch, t_batch)
    
    # 更新参数
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]
    
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)
    
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))

# 绘制图形
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()

从图形来看，随着epoch的前进（学习的进行），训练数据和测试数据的识别精度都提高了，且他们的识别精度没有差异，因此认为神经网络的学习没有发生过拟合。识别精度均超过90%。

这篇文章篇幅有点多，请读者好好理解，这篇文章我们主要介绍了损失函数、数值微分、求导、梯度、梯度更新等知识。欢迎关注微信公众号“Python生态智联”，学知识，享生活？

神经网络的学习

数据准备

训练数据

测试数据