[动态规划] Tree Construction

---

题目描述

Tree Construction

解题思路

首先我们可以确定这个题是一个 DP 题，所以我们就要去想这个题的状态转移怎么写，其实很简单
dp[i][j] 表示将第 i 个点到第 j 个点之间所有的点合在一起所花的费用
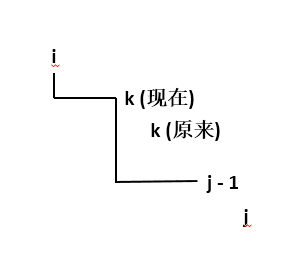
我们假设有三个点，i，k，k + 1，j，而这三个点是从左往右，从上往下排列的，如下图：

此时的 k 点就是合并 i 和 j 的一个任意中间的分割点，也就是 i 和 k 已经合在一起了，j 和 k + 1 也合在一起了
我们现在要合并 i 和 j，其实就是把 i，k 的合并点和 j，k + 1 的合并点相合并：

我们可以发现 $pm$ 的长度就是 $a[k].y - a[j].y$, $pn$ 的长度就是 $a[k + 1].x - a[i].x$
此时，我们的状态转移就已经得出了：

dp[i][j] 表示把第 i 个点到第 j 个点中的所有点都合起来所用的最小花费
dp[i][j] = dp[i][k] + dp[k + 1][j] + a[k].y - a[j].y + a[k + 1].x - a[i].x

得到状态转移，我们就可以求解了，但我们可以发现，这道题如果用朴素的DP求解是会超时的。所以，我们要加入平行四边形不等式优化

s[i][j]表示dp[i][j]的最佳决策点

这个 s[i][j] 有什么用处呢？
如果我们将 j 点去掉，合并 i 到 j - 1，那么 k 肯定就要往前移动，因为我们肯定要尽量让两边的平衡，所以 $s[i][j - 1] < s[i][j]$

同理，如果我们将 i 点去掉，合并 i + 1 到 j，那么 k 肯定就要往后移动，所以 $s[i + 1][j] > s[i][j]$

由此，我们就将 s[i][j] 控制在了一个较小的范围内，大大减少了程序的运行时间，我们枚举 k 的时候就只需要在 s[i][j - 1] 到 s[i + 1][j] 里去枚举就可以了
大家思考一下，如果 s[i][j - 1] 和 s[i + 1][j] 等于 0 怎么办？
这个时候我们就需要自己给 s 数组赋值：
如果 s[i][j - 1] 等于0，就赋值为 i ，如果 s[i + 1][j] 等于0，就赋值为 j
为什么要这么赋值呢？因为此时我们的边界就是在 i 和 j，我们赋值为边界值，就可以考虑进所有的情况了

参考代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<utility>
using namespace std;

#define M 1005
#define INF 0x3f3f3f3f

struct node{
    int x, y;
};
node a[M];

int n;
int s[M][M], dp[M][M];

void read(int &x) {
    x = 0; int f = 1; char s = getchar();
    while(s < '0' || s > '9') {if(s == '-') f = -1; s = getchar();}
    while(s >= '0' && s <= '9') {x = (x << 3) + (x << 1) + s - 48; s = getchar();}
    x *= f;
}

void wri(int x) {
    if(x < 0) {x = -x; putchar('-');}
    if(x / 10) wri(x / 10);
    putchar(x % 10 + 48);
}

void write(int x, char s) {
    wri(x);
    putchar(s);
}

int main() {
    while(scanf("%d", &n) != EOF) {
        memset(a, 0, sizeof(a));
        memset(s, 0, sizeof(s));
        for(int i = 1;i <= n;i ++)
            read(a[i].x), read(a[i].y);
        memset(dp, INF, sizeof(dp));
        dp[0][0] = 0;
        for(int i = n;i >= 1;i --) {
            dp[i][i] = 0;	//赋初值
            for(int j = i + 1;j <= n;j ++) {
                if(s[i][j - 1] == 0)	//判断 s[i][j - 1] 为0的情况
                    s[i][j - 1] = i;
                if(s[i + 1][j] == 0)	//判断 s[i + 1][j] 为0的情况
                    s[i + 1][j] = j;
                for(int k = s[i][j - 1];k <= s[i + 1][j];k ++)	//在限定的范围内枚举 k
                    if(dp[i][j] > dp[i][k] + dp[k + 1][j] + a[k].y - a[j].y + a[k + 1].x - a[i].x)	//如果有更有的结果，就更新 dp 数组，并改变这一位置的最佳决策点
                        dp[i][j] = dp[i][k] + dp[k + 1][j] + a[k].y - a[j].y + a[k + 1].x - a[i].x, s[i][j] = k;
            }
        }
        write(dp[1][n], '\n');
    }
    return 0;
}