第四章 游戏所需的三维数学
注:这个章节中矩阵和四元数部分的内容因涉及线性代数和计算机图形学等内容,略有抽象,博主才疏学浅,暂未参透。
4.1 在二维中解决三维问题
4.2 点和矢量
笛卡尔坐标系是游戏编程中最广泛使用的坐标系,但需谨记,应为当前问题选择最合适的坐标系。
大部分游戏程序员使用"矢量"一词来同时表示点(位置矢量)和矢量(纯方向性的矢量)。谨记,在心中必须清晰区分点和矢量。
笛卡尔基矢量(basis vector):3个正交单位矢量(orthogonal unit vector)(即矢量间相互垂直,且每个矢量的长度等于1)。称矢量i, j, k为笛卡尔基矢量。
矢量运算:
- 方向 + 方向 = 方向
- 方向 - 方向 = 方向
- 点 + 方向 = 点
- 点 - 点 = 方向
- 点 + 点 = 无意义(不要这么做!)
注:闵可夫斯基和(Minkowski sum)是针对点集的运算,可用于一些碰撞检测算法(如GJK算法),也可用于组合各形状的采样。
计算开方在多数计算机上都是很费时的运算,如果可以,游戏程序员应尽量改用模的平方。
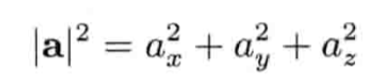
单位矢量(unit vector)即是模(长度)为1的矢量。
归一化(normalization)用矢量乘以其模的倒数。
法矢量(normal vector)是指矢量垂直与该表面。
注:法矢量一般为单位矢量,但此非必要条件。切记不要混淆归一化和法矢量两个术语。归一化后的矢量是任何拥有单位长度的矢量;而法矢量是指垂直于材质表面的矢量,其模是否为单位长度并不重要。
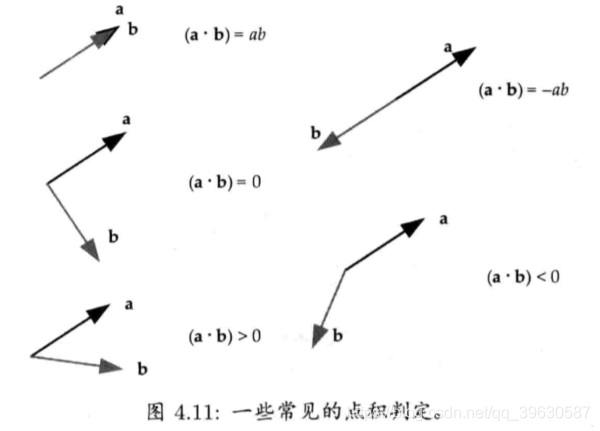
点积(dot product)又称为标量积或内积。
矢量投影(vector projection):若u为单位矢量,则点积(a · u)表示在u方向定义的无限长度直线上,a的投影长度。

点积判定(dot product test):
叉积(cross product)又称为矢量积或外积。
当视觉化一个叉积时,右手坐标系使用右手法则,左手坐标系使用左手法则。但是要记住,利手和数学计算并无关系,利手只影响如何使数字在三维空间中视觉化而已。
叉积不满足交换律,即先后次序是有影响的。叉积满足加法上的分配律。
笛卡尔基矢量之间有以下叉积关系:
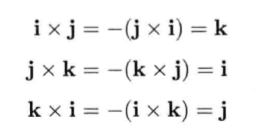
上述三个叉积定义了绕笛卡尔轴的正选方向。正旋自x到y(绕z轴)、自y到z(绕x轴)、自z到x(绕y轴)。
叉积可以用来求垂直于两个矢量的矢量、求三角形表面或其他平面的法矢量、计算力矩。
线性插值(linear interpolation)用来计算两个已知点的中间点。
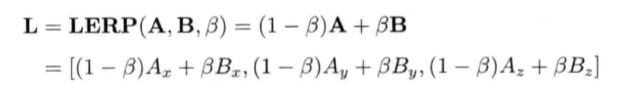
4.3 矩阵
特殊正交矩阵(special orthogonal matrix):或称各向同性矩阵(isotropic matrix)或标准正交矩阵(orthonormal matrix),是指3*3矩阵中的所有行及列矢量为单位矢量。这种矩阵表示纯旋转。
变换矩阵:是指用4*4矩阵表示任意三位变换包括平移、旋转和缩放的矩阵。这是对游戏工程师最为有用的矩阵。
放射矩阵(affine matrix):是一种4*4变换矩阵,它能维持直线在变换前后的平行性以及相对的距离比,但是不一定能维持直线在变换前后的绝对长度和角度。
矩阵乘法对游戏编程特别有用,因为可以把一连串变换预先计算为单一矩阵,再用该矩阵高效地变换大批矢量。仅当两矩阵的内维(inner dimension)相等时,两矩阵才可相乘。矩阵乘法不符合交换律。
点和矢量都可以表示为行矩阵(1*n)或列矩阵(n*1),其中n为使用中的空间维度。本来是可以任意选择行矢量或列矢量的,但次选择会影响矩阵乘法的书写次序。原因是矩阵乘法需要内维相等这一条件。
在欧氏几何空间,同一平面的两条平行线不能相交。然而,在透视空间里面,两条平行线可以相交,例如:火车轨道随着我们的视线越来越窄,最后两条平行线在无穷远处交于一点。
欧氏空间(或者笛卡尔空间)适合描述2D/3D几何,但却不适合处理透视空间的问题(实际上,欧氏几何是透视几何的一个子集合),二维笛卡尔坐标可以表示为(x,y),但如果一个点在无穷远处,这个点的坐标将会表示为(∞,∞),在欧氏空间中这是无意义的。为了解决这种问题,引入了齐次坐标(homogeneous coordinates)的概念。齐次坐标是游戏开发和图形学的重要概念。
基础变换矩阵

注:4*4仿射矩阵的最右侧必然是一列[0 0 0 1]^T的矢量(前提是行矢量惯例,从左至右的习惯),因此游戏程序员可以略去第四列,以节省内存。
平移

旋转

缩放

基的变更(change of basis):将物体的位置、定向和缩放从某个坐标系转换至另一个坐标系。

基变更矩阵是由平移及3个笛卡尔基矢量组成的,故任何4*4仿射矩阵,都可以用反向思维,从恰当的矩阵行(若使用列矢量则为矩阵列)中获取子空间基矢量i, j, k。
4.4 四元数
使用矩阵表示旋转的问题:
- 矩阵需要9个浮点值表示旋转,但是旋转只有三个自由度(degree of freedom, DOF)——偏航角、俯仰角、滚动角。
- 使用矢量矩阵算法来旋转矢量,需3个点积,即共9个乘数及6个加数。
- 计算在两个已知旋转之间某个比例的旋转时,若以矩阵表示A和B的定向,要计算中间值(插值)是很困难的。
而采用四元数(quaternion)表示旋转则能克服上述问题。
单位四元数能够代表三维旋转,可以视觉化为三维矢量加上第四维的标量坐标。单位四元数可以写成

注:非单位长度的两个四元数相加不能代表三维旋转,除非采用某种党阀缩放到符合单位长度的要求。
四元数乘法有几种,书中只讨论与三维旋转应用相关的乘法——格拉斯曼积(Grassmann product)。
给定两个四元数p和q,分别代表旋转P和Q,则pq代表合成旋转(即旋转Q之后再旋转P)。
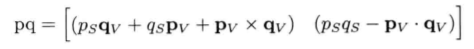
四元数的共轭(conjugate):矢量部分求反,但保持标量部分不变。
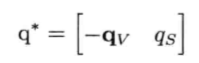
逆四元数:

由于实现三维旋转都是单位四元数,即|q|=1,这种情况下,共轭和逆四元数是相等的。这就意味着,计算逆四元数会比计算3*3逆矩阵快得多。
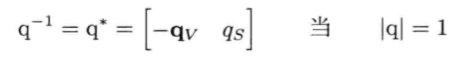
以四元数旋转矢量:
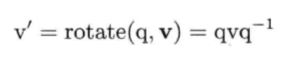
任何三维旋转都可以从3*3矩阵表达方式R和四元数表达方式q之间自由转换。对于四元数q=[q v]=[x y z w],可用如下公式求R:
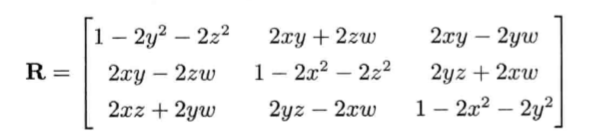
旋转性的线性插值就是套用四维矢量的线性插值(LERP)至四元数。
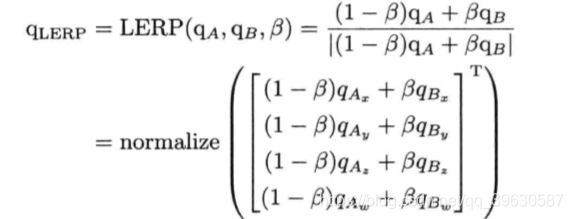
LERP的问题在于,它没有考虑到四元数实际是四维超球(hypersphere)上的点。LERP是沿超球的弦上进行插值,这会导致插值以恒定速度改变时,旋转动画并非以恒定角速度进行,而实际应该是在超球面上插值才对。
球面线性插值(spherical linear interpolation,SLERP):

其中,两个单位四元数之间的夹角,可以用四维点积求得:
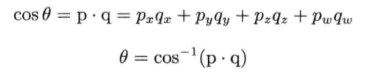
4.5 比较各种旋转表达方式
欧拉角
欧拉角:由三个标量值组成(偏航角、俯仰角、滚动角),欧拉角使用三个浮点数,而且可以直观的进行视觉化。
使用欧拉角可以方便的对单轴旋转进行LERP(对于任意轴则不然)。
欧拉角最著名的问题就是万向节死锁(gimbal lock):当旋转90度时,三主轴中的一个会与另一主轴完全对齐。
欧拉角的另一个问题是,先绕哪根轴旋转,再绕哪根轴旋转,旋转的先后次序对结果是有差别的。
3*3矩阵
优点:可以直接适于点或矢量。不受万向节死锁影响。可独一无二地表达任意旋转。
缺点:相对于欧拉角,旋转矩阵需要大量存储空间(9个浮点数),且不易实现插值。
轴角
轴角表示法:一个以单位矢量定义的旋转轴,再加上一个标量定义的旋转角,也可用来表示旋转。
优点:表达直观,而且紧凑(只需4个浮点数)
缺点:不能简单地进行插值。不能直接施于点或矢量。
四元数
轴角与四元数的表达形式虽然类似,但是意义不同。
优点:可以串接,并直接施于点和矢量。能够轻易地使用LERP或SLERP进行旋转插值
SQT变换
四元数只能表示旋转,而4*4矩阵则可以表示任意仿射矩阵(旋转、平移、缩放)。当四元数结合平移矢量和缩放因子,就可以的得到一个4*4仿射矩阵,这就是所谓的SQT变换,因为其包含缩放(scale)因子、表示旋转的四元数(quaternion)和平移(translation)矢量。

优点:体积较小,统一算缩放需要8个浮点数,非统一缩放需要10个浮点数。容易实现插值。
对偶四元数
对偶四元数也可以完整的表示涉及旋转、平移、缩放的变换,其4个分量并非实数,而是对偶数。对偶数(dual number)可以写成非对偶部(non-dual part)和对偶部(dual part)。因为每个对偶数都能表示为两个实数(非对偶部和对偶部),所以对偶四元数可表示为含有8个元素的矢量,或者表示为两个普通四元数之和。
旋转和自由度
自由度(degree of freedom, DOF)是指物体有对少个相互独立的可变状态(位置和定向)。
6个DOF指的是一个三维物体(在其运动没受人工约束的情况下)在平移上有3个DOF(沿x/y/z轴),在旋转上也有3个DOF(沿x/y/z轴)。
所有的三维旋转表达方式都有三个3个或以上的浮点参数,但一些表达方式也会对参数加上一个或一个以上的约束。三维旋转的DOF总是3:
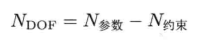
4.6 其他数学对象
- 直线(line)、射线(ray)、线段(line segment)
- 球体(sphere)
- 平面(plane)
- 轴对齐包围盒(axis-aligned bounding box, AABB)
- 定向包围盒(oriented bounding box, OBB)
- 平截头体(frustum)
4.7 硬件加速的SIMD运算
暂时略过
4.8 产生随机数
随机数产生器仅仅是非常复杂而已,这些序列其实是完全确定性的(deterministic)伪随机序列。随机数产生器的好坏,取决于其产生多少个数字之后会重复(即序列的周期),以及该序列在多个著名测试中的表现。
线性同余产生器(linear congruential generator, LGC):有些平台会使用此算法来实现标准C语言库的rand()函数,但LGC并不能产生特别高质量的伪随机序列。
梅森旋转算法(Mersenne Teister, MT):为改进LGC的重多问题而设计。