一文看懂BP神经网络的基础数学知识

看懂本文需要的基础知识有：

能够理解最基本的最优化问题（例如最小二乘法优化）
学习过高数和线性代数，对数学符号有概念
一定的编程基础
最好明白感知器的概念
神经网络的基本知识

1.0 历史与发展

线性神经网络只能解决线性可分的问题，这与其单层网络的结构有关。 BP 神经网络是包含多个隐含层的网络，具备处理线性不可分问题的能力。在历史上，由于一直没有找到合适的多层神经网络的学习算法，导致神经网络的研究一度陷入低迷。 M.Minsky 等仔细分析了以感知器为代表的神经网络系统的功能及局限后，于 1969 年出版了 “ Perceptron ”一书，指出感知器不能解决高阶谓词问题，他们的观点加深了人们对神经网络的悲观情绪。 20世纪80年代中期， Rumelhart，MicClelland 等成立了 Parallel Distributed Procession(PDP) 小组，提出了著名的误差反向传播算法（ Error Back Propagtion,BP)，解决了多层神经网络的学习问题，极大促进了神经网络的发展，这种神经网络就被称为BP神经网络。
感知器、线性神经网络、BP网络与径向基神经网络都属于前向网络，其中BP网络和径向基网络属于多层前向神经网络。 BP网络是前向神经网络的核心部分，也是整个人工神经网络体系中的精华，广泛应用于分类识别、逼近、回归、压缩等领域。在实际应用中，大约80%的神经网络模型采取了 BP网络或BP网络的变化形式。

划重点：

BP神经网络有/是

多个隐藏层
线性不可分
误差反向传播算法
前向网络

1.1 BP神经网络的结构

BP神经网络一般是多层的，与之相关的另一个概念是多层感知器(Multi-Layer perceptron,MLP)。多层感知器除了输入层和输出层意外，还具有若干个隐含层。多层感知器强调神经网络在结构上由多层组成，**BP神经网络也是一种多层感知器，它强调网络采用误差反向传播的学习算法。**大部分情况下多层感知器采用误差反向传播的算法进行权值调整，因此两者一般指的是同一种网络，在本书中两个概念同时使用。
BP神经网络的隐含层可以为一层或多层，一个包含2层隐含层的BP神经网络的拓扑结构如图6-1

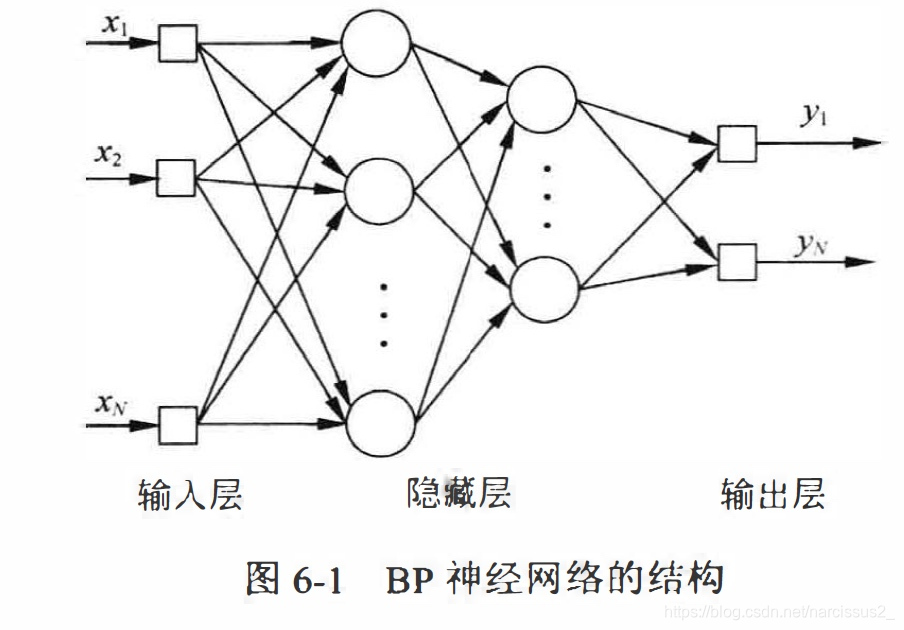
在这里插入图片描述

BP神经网络有如下特点

(1) 网络由多层构成，层和层之间全连接，同一层之间的神经元无连接。多层网络的设计，使BP网络能够从输入中挖掘更多信息，完成更复杂的任务。
(2) BP网络的传递函数必须可微分。因此，感知器的传递函数——二值函数在这里没有用武之地。BP网络一般使用sigmoid函数或线性函数作为传递函数。根据输出值是否包含负值，sigmoid函数可分为Log-sigmoid函数和Tan-Sigmoid函数。一个简单的Log-Sigmoid函数可由下式确定。 $f(x)=\frac{1}{1+e^{-x}}$ 其中x的范围包含整个实数域，函数值在0~1之间，具体应用时可以增加参数，以控制曲线的位置和形状。Log-Sigmoid函数和Tan-sigmoid函数的曲线分别如图6-2和6-3。

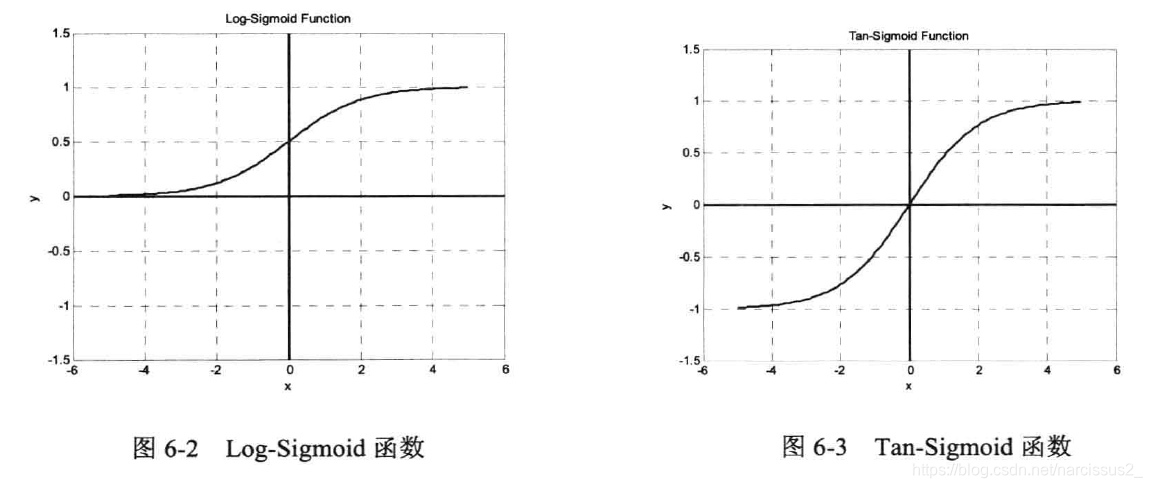
从图中可以看出**，Sigmoid函数是光滑、可微的函数，在分类时它比线性函数更精确，容错性较好。** **它将输入从负无穷到正无穷的范围映射到（一1,1）或（0,1）区间内，具有非线性的放大功能。**以正半轴为例，在靠近原点处，输入信号较小，此时曲线上凸，输出值大于输入值：随着信号增大，非线性放大的系数逐渐减小。Sigmoid函数可微的特性使它可以利用梯度下降法。在输出层，如果采用Sigmoid函数，将会把输出值限制在一个较小的范围，因此，BP神经网络的典型设计是隐含层采用Sigmoid函数作为传递函数，而输出层则采用线性函数作为传递函数。
(3) 采用误差反向传播算法(Back-Propagation Algorithm)进行学习。在BP网络中，数据从输入层经隐含层逐层向后传播¹，训练网络权值时，则沿着减少误差的方向²,从输出层经过中间各层逐层向前修正网络的连接权值。
注意：切记要区分”误差反向传播“与”反馈神经网络“。在BP网络中，”反向传播“指的是误差信号反向传播，修正权值时，网络根据误差从后向前边层进行修正。BP神经网络属于多层前向网络，工作信号始终正向流动，没有反馈结构。在本书第9章中会专门介绍反馈神经网络，包括Hopfield网络、Elman网络等。在反馈神经网络中，输出层的输出值又连接到输入神经元，作为下一次计算的输入，如此循环迭代，直到网络的输出值进入稳定状态为止。

划重点：

sigmoid函数
层和层全连接
函数可微分
误差反向传播
权值从后向前修正
信号正向流动
两张图

1.2 BP网络的学习算法

1.2.1 BP网络学习算法的大体感知

确定BP网络的层数和每层的神经元个数
确定各层之间的权值系数。
1. 训练时先使用随机权值。
2. 输入学习样本后得到输出。
3. 然后反复修改使误差不再下降，训练完成
4. 修改权值有不同的规则。标准的BP网络沿着误差性能函数梯度的反方向。原理与LMS算法比较类似，属于最速下降法。此外，还有一些改进算法，动量最速下降法，拟牛顿法。

1.2.1 最速下降法

最速下降法即LMS概念：

梯度下降法又称为梯度下降法，是一种可微函数最优化算法。
LMS算法即最小均方误差算法（Least Mean Square Algorithm）。
LMS就是目标函数为均方误差的最速下降法。

最速下降法原理

最速下降法基于这样的原理：对于实值函数F(x），如果F(x）在某点X₀处有定义且可微，则函数在该点处沿着梯度相反的方向 $-\nabla F(x_0)$ 下降最快。因此，使用梯度下降法时，应首先计算函数在某点处的梯度，再沿着梯度的反方向以一定的步长调整自变量的值。

假设 $x_1=x_0-\eta \nabla F(x_0)$ ，当步长 $\eta$ 足够小时，必有以下公式 $F(x_1)<F(x_0)$
因此，只需给定一个初始值 $x_0$ 和步长 $\eta$ ，根据 $x_{n+1}=x_n-\eta\nabla F(x_n)$
就可以得到一个自变量x的序列，并满足 $F(x_{n+1})<F(x_{n})<...<F(x_0)$
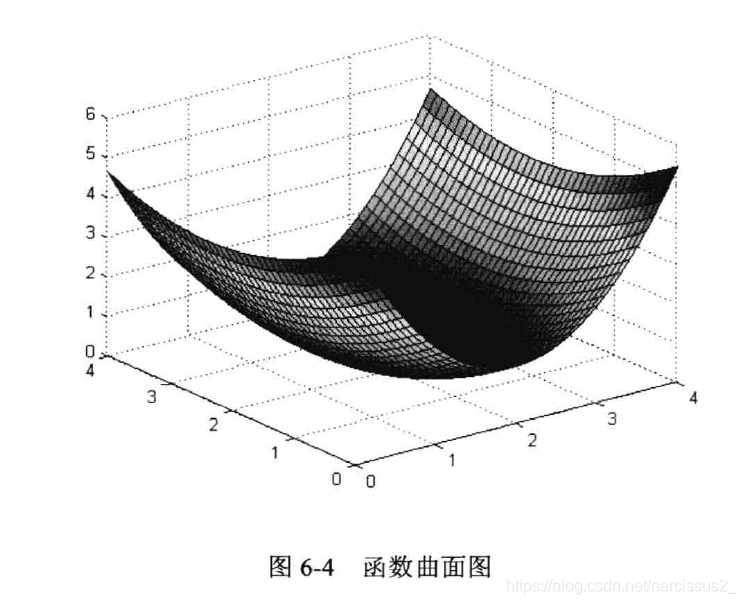
反复迭代，就可以求出函数的最小值。梯度下降法可以认为是沿着垂直于等值方向向最小值所在位置移动。对于可微函数，最速下降法是求最小值或极小值的一种有效方法。如图6-4与图6-5所示，目标函数是下式定义的二维函数： $z=(x-2)^2+(y/2-1.2)$
函数呈现碗状，中间低，四周高，以任意一点为初始位置，使用最速下降法都能找到最低点。

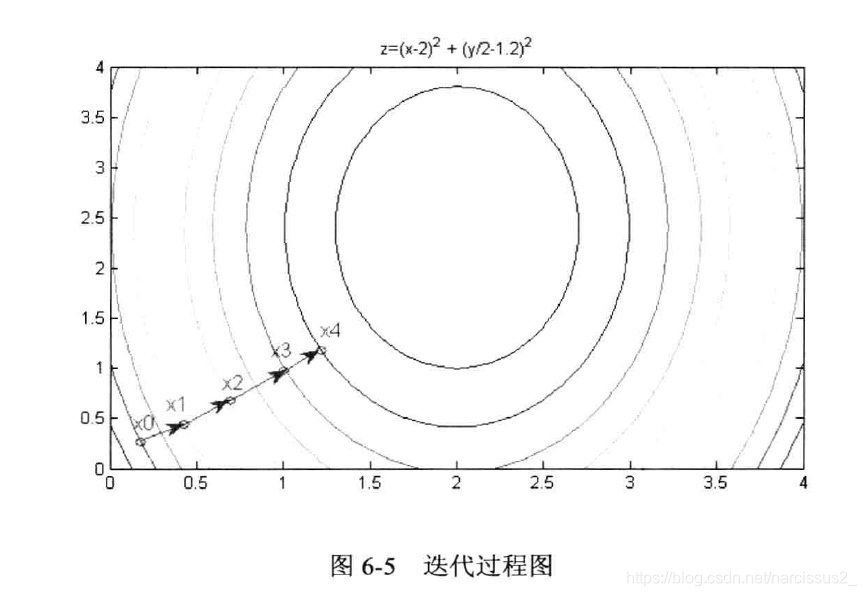
在这里插入图片描述

最速下降法的缺陷

目标函数必须可微分。
如果最小值附近平摊，算法会停留很久，收敛很慢。可能出现"之"字下降。
对于包含多个极小值的函数，所获得的结果依赖于初始值。算法可能陷入局部极小值。

一些解释

$\nabla$ 是什么：这个是梯度的意思，梯度可以认为是一阶导数的方向，那沿着导数方向下降是最快的了，没有概念的话可以自己画个二次函数，搞个切线，然后沿着负梯度下降一下
$\eta$ 就是步长，就你下降的时候一步走多长。
这两张图仔细看看就应该能看懂了。
误差能量事实上就是均方误差的方程。

1.2.2 最速下降BP法

标准的BP网络是用最速下降法来调制各层权值。下面以三层BP网络为例推导标准BP网络的权值学习算法。

1. 变量定义

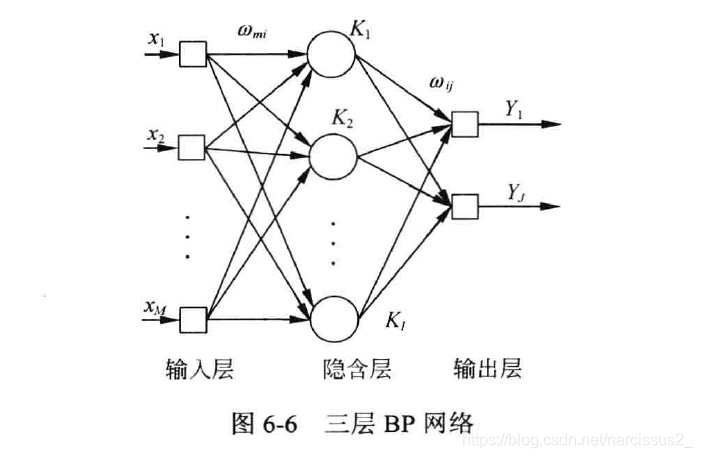
在三层BP网络中，假设输入神经元个数为M，隐含层神经元个数为I，输入层神经元个数为J。输入层第m个神经元记为x_m，隐含层第i个神经元记为k_i，输入层第j个神经元记为y_j。从x_m到k_i的连接权值为 $\omega _{mi}$ ,从k_i到y_j的连接权值为 $\omega _{ij}$ 。隐含层传递函数为sigmoid函数，输出层传递函数为线性函数，网络结构如图6-6所示。
上述网络接受一个长为M的向量作为输入，最终输出一个长为J的向量。用μ和ν分别表示每一层的输入和输出，如 $u^1_I$ 表示第I层(即隐含层）的第一个神经元的输入。网络的实际输出为： $Y(n)=[v^1_J,v^2_J,...,v^J_J]$
网络的期望输出为： $d(n)=[d_1,d_2,...,d_j]$
n为迭代次数。第n次迭代的误差信号定义为： $e_j(n)=d_j(n)-Y_j(n)$
将误差能量定义为： $e(n)=\frac{1}{2}\sum_{j=1}^Je^2_j(n)$

一些解释：

上面没写神经网络的输入向量，可以思考一下神经网络的输入向量是长什么样的。（很简单）
sigmoid函数就相当于在隐藏层激活权值的激活程度。
可以思考一下为什么在输出层最后是线性累加？(别的累加方式行不行呢？一般用哪种？）

2.工作信号正向传播

输入层的输出等与整个网络的输入信号： $v^m_M(n)=x(n)$
隐含层第i个神经元的输入等于 $v^m_M(n)$ 的加权和(看图)： $u^i_I(n)=\sum_{m=1}^M\omega _{m_i}(n)v_M^m(n)$
假设f(·)为sigmoid函数，则隐含层第I个神经元的输出等于： $v^i_I(n) = f(u^i_I(n))$
输出层的第j个神经元的输入等于 $v^i_I(n)$ 的加权和: $u^j_J(n)=\sum_{i=1}^Iw_{ij}(n)v^i_I(n)$
输出层第j个神经元的输出等于： $v^j_J(n) = g(u^j_J(n))$
网络的总误差： $e(n)=\frac{1}{2}\sum_{j=1}^Je^2_j(n)$

一些解释

可以看到是先加权，然后再用sigmoid函数映射到0~1上
加权就是简单的线性累加。
f函数指sigmoid函数(作用于隐藏层)，g函数指的是线性求和函数(作用于输出层)。

3. 误差信号反向传播

在权值阶段，沿着网络逐层反向调整。

(1) 首先调整隐藏层与输出层之间的权值 $\omega_{ij}$ (就是第i行第j列的节点的权值)。

根据最速下降法，应计算误差对 $\omega_{ij}$ 的梯度 $\frac{\phi e(n)}{\phi w_{ij}(n)}$ （一式), 再沿着该方向反向进行调整(二式)(三式)： $△w_{ij}(n)=-\eta \frac{\phi e(n)}{\phi w_{ij}(n)}$ $w_{ij}(n+1)=△w_{ij}(n)+w_{ij}(n)$
梯度可以由求偏导得到。根据微分的链式规则，有(四式)： $\frac{\phi e(n)}{\phi w_{ij}(n)}=\frac{\phi e(n)}{\phi e_j(n)}\cdot \frac{\phi e_j(n)}{\phi v^j_J(n)} \cdot \frac{\phi v^j_J(n)}{\phi u^j_J(n)} \cdot \frac{\phi u^j_J(n)}{\phi w_{ij}(n)}$
由于e(n)是 $e_j(n)$ 的二次函数，其微分为一次函数(五式)(六式)： $\frac{\phi e(n)}{\phi e_j(n)} = e_j(n)$ $\frac{\phi e(n)}{\phi v^j_J(n)} = -1$
输出层传递函数的导数(七式)：
$\frac{\phi v^j_J(n)}{\phi u^j_J(n)}=-e_j(n)g''(u^j_J(n))v^i_I(n)$
权值修正量为(八式):
$\Delta w_{ij}(n)=\eta e_j(n)g'(u^j_J(n))v^i_I(n)$
引入局部梯度的定义(九式)：
$\delta^i_J=-\frac{\phi e(n)}{\phi u^j_J(n)}=-\frac{\phi e(n)}{\phi e_j(n)}\cdot \frac{\phi e(n)}{\phi v^j_J(n)}\cdot \frac{\phi v^j_J(n)}{\phi u^j_J(n)}=e_j(n)g'(u^j_J(n))$
因此，权值修正量可以表示为（十式)： $\Delta w_{ij}(n)=\eta \delta^j_Jv^i_I(n)$
局部梯度知名权值所需要的变化。神经元的局部梯度等于该神经元的误差信号与传递函数导数的乘积。在输出层，传递函数一般为线性函数，因此其导数为1：(十一式) $g'(u^j_J(n))=1$ 代入上式，可得(十二式) $\Delta w_{ij}(n)=\eta e_j(n)v^i_I(n)$ 输出神经元的权值修正相对简单。

详细的解释：

首先强调我们的直接目的是调整隐藏层与输出层之间的权值 $w_{ij}$ ，根本目的是减小误差。J代表的是输出层，i代表的是隐藏层。
这里只是在调整神经元的第i行第j列的一个权值。
先看一式，误差函数对 $w_{ij}$ 求偏导，误差函数的构成是{实际输出-期望输出}，而实际输出=权值( $w_{ij}$ )*输入，建议尝试自己将误差函数全面展开后看一看。
二式指的是梯度方向，三式指的是得到下次迭代权值的方程，它由上一次迭代权值加上梯度方向增长的权值构成。
四式：先解释什么是链式法则——链式法则就是解决复合函数求导数问题的方法，具体举个例子就明白了：
例题：求导 $y=sin(x^2+1)$
5.2. 链式求导: $f(x)=sin(x), g(x)=x^2+1$
5.3. 则求导变成了 $f(g(x))'=f'(g(x))g'(x)=[sin(x^2+1)]'\cdot 2x=2cos(x^2+1)x$
5.4. 我们可以这样来表示整个过程， $\frac{\phi y}{\phi x}=\frac{\phi y}{\phi z}\cdot \frac{\phi z}{\phi x}$ ，这类似于分数的约分。
5.5. 所以用人话解释五式就是，这个(误差能量函数对于每个权值求偏导)=(误差能量对误差信号j求导)×(误差信号对第j个神经元的输出求偏导)×(第j个神经元的输出对第j个神经元加权和去偏导)×(第j个神经元的加权和对于权值j求偏导)
五式：这个你就当成对 $\frac{1}{2}x^2$ 进行求导就对了
六式： $e_j(n)=d_j(n)-v_j(n)$ 对 $v_j$ 求导，求出来就是-1呗。
七式：输出层的第j个神经元的输出对加权和进行求导（ $v^j_J(n) = g(u^j_J(n))$ ），可见经过线性加权和后，输出层还进行了函数g操作，求导遵从链式法则；八式加权和对权值求导( $u^j_J(n)=\sum_{i=1}^Iw_{ij}(n)v^i_I(n)$ )，输出的当然就是隐藏层第j个神经元输出的值了。
这个 $g$ 是输出层的传递函数，它一般都是一次函数，所以我们直接把他的导数当成1就好了，于是就有了第十二式，这下问题就全解决了。

(2)误差信号向前传播，对输入层和隐藏层之间的权值 $w_{mi}$ 进行调整

与上一步类似应有 $\Delta w_{ij}(n)=\eta e_j(n)v^i_I(n)$
$v^m_M(n)$ 为输入神经元的输出， $v^m_M(n)=x^m(n)$ .
$\delta^i_I$ 为局部梯度，定义为 $\delta^i_I=-\frac{\phi e(n)}{\phi u^i_I(n)}=-\frac{\phi e(n)}{\phi v^i_I(n)} \cdot \frac{\phi v^i_I(n)}{\phi u^i_I(n)}=-\frac{\phi e(n)}{\phi v^i_I(n)}f'(u^i_I(n))$ f(g)为sigmoid传递函数。由于隐藏层不可见，因此无法直接求解误差对该层输出值的偏导数 $\frac{\phi e(n)}{\phi v^i_I(n)}$ 。这里需要使用上一步计算中求得的输出层节点的局部梯度： $\frac{\phi e(n)}{\phi v^i_I(n)}=\sum_{j=1}^J\delta ^j_Jw_{ij}$ 故有 $\delta ^i_I=f'(u^i_I(n))\sum_{j=1}^J\delta ^j_Jw_{ij}$
(再次强调,i是隐藏层参数，J是输出层参数，调整权值的过程是先后再前的)
至此，三层BP网络的一轮全职就调整完成了。调整规则可总结为：
权值调整量： $\Delta w$ =学习率 $\eta$ 局部梯度 $\delta$ 上一层输出信号 $v$
当输出层传递函数为线性函数时，输出层与隐藏层间权值调整的规则类似于线性神经网络的权值提走二行规则。BP神经网络的复杂在于，隐藏层与隐藏层之间、隐藏层与输入层之间调整权值时，局部梯度的计算需要用到上一步计算结果。前一层的局部梯度是后一层局部梯度的加权和。也正是这个原因，BP网络学习权值时只能从后向前依次计算。

基本步骤回顾

收集数据，得到输入和期望输出。
初始化权值 $w_{11}—w_{ij}$ ，初始化步长 $\eta$
在迭代的时候，更新权值修正量 $\Delta w_{ij}(n)=\eta e_j(n)v^i_I(n)$
等待权值变化收敛，迭代结束，获得神经网络。

参考资料：《Matlab神经网络原理与实践精解》