文章目录

第二章:感知器(perceptron)
2.1 感知器是什么
感知器接受多个输入信号,输出一个信号。
如图是一个接收两个输入信号的感知器。
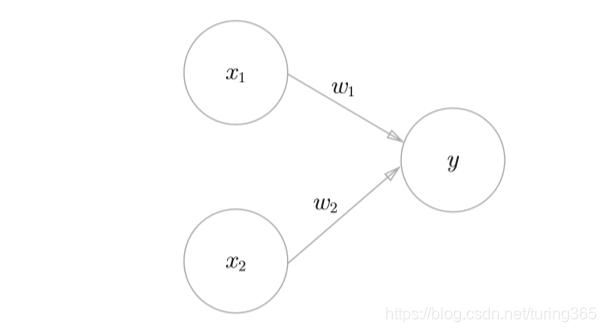
, 是输入信号, 是输出信号, , 是权重。
图中的圆圈称为“神经元”(或“节点”)。输入信号被送往神经元时,会被分别乘以固定的权重( , )。神经元会 计算传送过来信号的总和,只有当这个总和超过某个界限时,才会输出1。将这个界限称为阈值,用 表示。
就上述内容用数学公式表示:
感知器的多个输入信号都有各自的权重,这些权重发挥控制各个信号的重要性的作用。也就是说,权重越大,对应该权重的信号的重要性越高。
2.2 简单的逻辑电路
2.2.1 与门
与门(AND gate)有两个输入和一个输出。下图是与门的真值表:
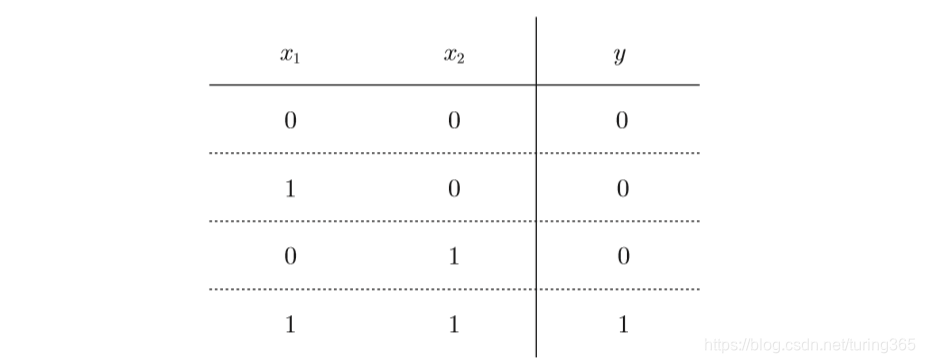
下面用感知机来表示与门。需要做的就是确定能满足上图的真值表的 、 、 的值。
那么,设定什么样的值才能制作出满足上图的条件的感知机呢? 实际上,满足上图的条件的参数的选择方法有无数多个。比如,当
(
,
,
) = (0.5, 0.5, 0.7)时,可以满足上图的条件。此外,当(
,
,
) 为(0.5,0.5, 0.8)或者(1.0, 1.0, 1.0)时,同样也满足与门的条件。设定这样的参数后,仅当
和
同时为1时,信号的加权总和才会超过给定的阈值
。
2.2.2 与非门和或门
与非门(NAND gate)颠倒了与门的输出。真值表如下:
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
只要把实现与门的参数值的符号取反, 就可以实现与非门。
或门是只要有一个输入信号是1,输 出就为1的逻辑电路。真值表如下:
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
如上所示,我们已经知道使用感知机可以表示与门、与非门、或门的逻辑电路。重要的一点是:与门、与非门、或门的感知机构造是一样的。 实际上,3个门电路只有参数的值(权重和阈值)不同。也就是说,相同构造的感知机,只需通过适当地调整参数的值,就可以变身为与门、与非门、或门。
2.3 感知器的实现
2.3.1 简单的实现
现在,我们用Python来实现刚才的逻辑电路。这里,先定义一个接收参数x1和x2的AND函数。
def AND(x1,x2):
w1,w2,theta=0.5,0.5,0.7
tmp=x1*w1+x2*w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1
在函数内初始化参数w1、w2、theta,当输入的加权总和超过阈值时返回1, 否则返回0。我们可以确认一下输出结果是否真值表所示:
AND(0, 0) # 输出0
AND(1, 0) # 输出0
AND(0, 1) # 输出0
AND(1, 1) # 输出1
这样就实现了与门。按照同样的步骤,也可以实现与非门和或门,不过对它们的实现稍作修改。
2.3.2 导入权重和偏置
刚才的与门的实现比较直接、容易理解,但是考虑到以后的事情,我们将其修改为另外一种实现形式。
在此之前,首先把之前2.1的式子的
换成
,于是就可以用下面的式子来表示感知机的行为:
2.1的式子和上面的式子虽然有一个符号不同,但表达的内容是完全相同的。此处, 称为偏置, 和 称为权重。
如上式所示,感知机会计算输入信号和权重的乘积,然后加上偏置,如果这个值大于0则输出1,否则输出0。
下面,我们使用NumPy,按上式的方式实现感知机。在这个过程中,我们用Python的解释器逐一确认结果。
>>> import numpy as np
# 输入
>>> x = np.array([0, 1])
# 权重
>>> w = np.array([0.5, 0.5])
# 偏置
>>> b = -0.7
>>> w*x
array([ 0. , 0.5])
>>> np.sum(w*x)
0.5
>>> np.sum(w*x) + b
-0.19999999999999996
# 大约为-0.2(由浮点小数造成的运算误差)
如上例所示,在NumPy数组的乘法运算中,当两个数组的元素个数相同时, 各个元素分别相乘,因此 的结果就是它们的各个元素分别相乘([0, 1] * [0.5, 0.5] => [0, 0.5])。之后,np.sum(w*x)再计算相乘后的各个元素的总和。 最后再把偏置加到这个加权总和上,就完成了上式的计算。
2.3.3 使用权重和偏置的实现
使用权重和偏置,可以像下面这样实现与门。
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
这里把 命名为偏置 ,但是注意,偏置和权重 、 的作用是不一样的。
具体地说,
和
是控制输入信号的重要性的参数,而偏置是调整神经元被激活的容易程度(输出信号为1的程度)的参数。
比如,若b为−0.1,则只要输入信号的加权总和超过0.1,神经元就会被激活。但是如果b 为−20.0,则输入信号的加权总和必须超过20.0,神经元才会被激活。像这样,偏置的值决定了神经元被激活的容易程度。另外,这里我们将
和
称为权重, 将b称为偏置,但是根据上下文,有时也会将b、
、
这些参数统称为权重。
下面是与非门与或门的实现:
def NAND(x1n,x2):
x=np.array([x1n,x2])
# 权重与偏置与AND不同
w=np.array([-0.5,-0.5])
b=0.7
tmp=np.sum(w*x)+b
if tmp<=0:
return 0
else:
return 1
def OR(x1,x2):
x=np.array([x1,x2])
w=np.array([0.5,0.5])
b=-0.2
tmp=np.sum(w*x)+b
if tmp<=0:
return 0
else:
return 1
2.4 感知器的局限性
2.4.1 异或门
异或的真值表如下:
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
仅当 或 中的一方为1时你,才会输出1。要用感知机实现这个异或门,应该设定什么样的权重参数呢?
实际上,用前面介绍的感知器是无法实现这个异或门的。为什么用感知器可以实现与门、或门,却无法实现异或门呢?下面我们尝试通过画图来思考其中的原因。 首先,我们试着将或门的动作形象化。或门的情况下,当权重参数(b,
,
) = (−0.5, 1.0, 1.0)时,可满足或门的真值表条件。此时,感知器可用下面的式表示:
上式表示的感知器会生成由直线−0.5 + x1 + x2 = 0分割开的两个空间。其中一个空间输出1,另一个空间输出0,如图所示:
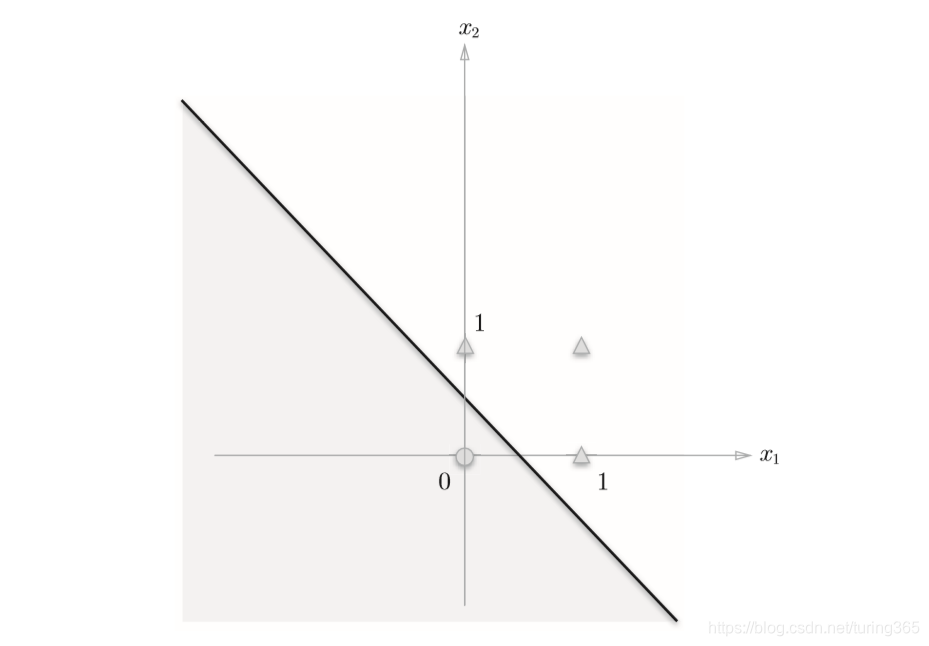
或门在(x1,x2) = (0, 0)时输出0,在(x1,x2)为(0,1)、(1,0)、(1,1)时输出1。上图中,○表示0,△表示1。如果想制作或门,需要用直线将图中的○和△分开。实际上,刚才的那条直线就将这4个点正确地分开了。
那么,换成异或门的话会如何呢?能否像或门那样,用一条直线作出分割下面图中的○和△的空间呢?

可以发现,想要用一条直线将图中的○和△分开,无论如何都做不到。事实上, 用一条直线是无法将○和△分开的。
2.4.2 线性和非线性
上面图中的○和△无法用一条直线分开,但是如果将“直线”这个限制条件去掉,就可以实现了。
比如,我们可以像下图那样,作出分开○和△的空间。
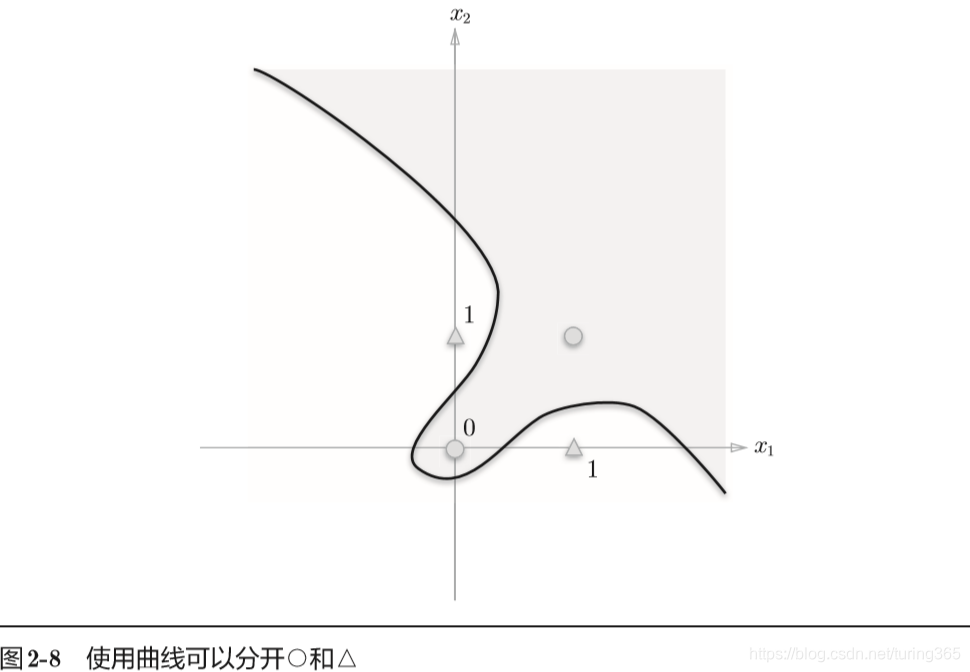
感知器的局限性就在于它只能表示由一条直线分割的空间。上图这样弯曲的曲线无法用感知机表示。另外,由上图这样的曲线分割而成的空间称为非线性空间,由直线分割而成的空间称为线性空间。
2.5 多层感知器
感知机不能表示异或门让人深感遗憾,但也无需悲观。实际上,感知机的绝妙之处在于它可以“叠加”。
2.5.1 已有门电路的组合
异或门可以通过下图所示的配置来实现。这里,x1和x2表示输入信号, y表示输出信号。x1和x2是与非门和或门的输入,而与非门和或门的输出则是与门的输入。

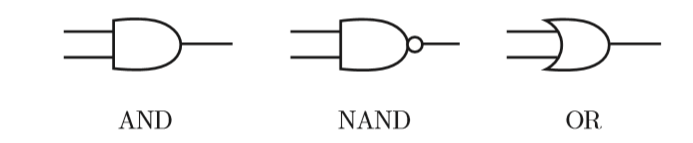


现在,我们来确认一下上图的配置是否真正实现了异或门。这里,把 s1作为与非门的输出,把s2作为或门的输出,填入真值表中。结果如图所示,观察x1、x2、y,可以发现确实符合异或门的输出。

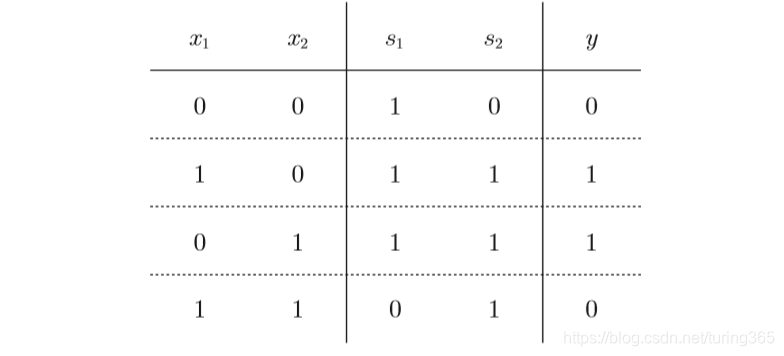
2.5.2 异或门的实现
根据上面的配置,可以来实现异或:
def XOR(x1,x2):
s1=NAND(x1,x2)
s2=OR(x1,x2)
y=AND(s1,s2)
return y
这个异或函数会输出预期的结果:
XOR(0, 0) # 输出0
XOR(1, 0) # 输出1
XOR(0, 1) # 输出1
XOR(1, 1) # 输出0
这样,异或门的实现就完成了。下面我们试着用感知机的表示方法(明确地显示神经元)来表示这个异或门,结果如图所示

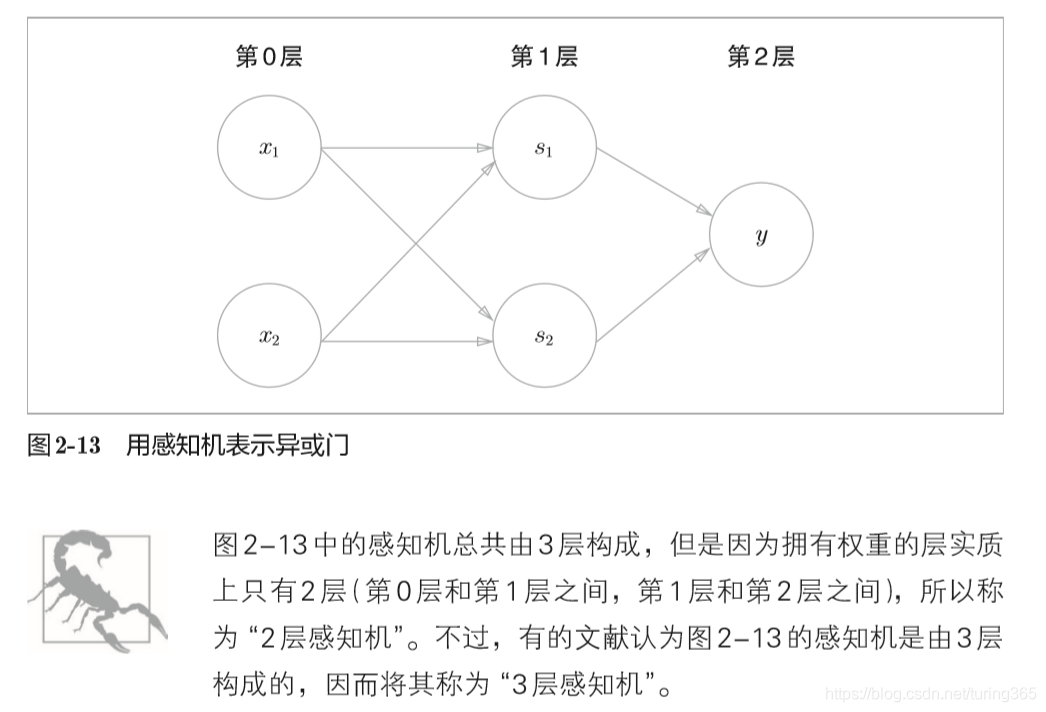
如图所示,异或门是一种多层结构的神经网络。这里,将最左边的 一列称为第0层,中间的一列称为第1层,最右边的一列称为第2层。
上图所示的感知机与前面介绍的与门、或门的感知机形状不同。实际上,与门、或门是单层感知机,而异或门是2层感知机。叠加了多 层的感知机也称为多层感知机(multi-layered perceptron)。
在上图所示的2层感知机中,先在第0层和第1层的神经元之间进行 信号的传送和接收,然后在第1层和第2层之间进行信号的传送和接收,具体如下所示。
- 第0层的两个神经元接收输入信号,并将信号发送至第1层的神经元。
- 第1层的神经元将信号发送至第2层的神经元,第2层的神经元输出y。
像这样,在异或门的感知机中,通过这样的结构(2层结构),感知机得以实现异或门。这可以解释为“单层感知机 无法表示的东西,通过增加一层就可以解决”。也就是说,通过叠加层(加深层),感知机能进行更加灵活的表示。