概率算法
随机性(randomness)是偶然性的一种形式,是某一事件集合中的各个事件所表现出来的不确定性。产生某一随机性事件集合的过程,是一个不定因子不断产生的重复过程,但它可能遵循某个概率分布。
随机序列(random sequence),更确切的,应该叫做随机变量序列,也就是随机变量形成的序列。一般的,如果用X1,X2……Xn代表随机变量,这些随机变量如果按照一定顺序出现,就形成了随机序列。这种随机序列具备两个关键的特点:其一,序列中的每个变量都是随机的;其二,序列本身就是随机的。
在现实计算机上无法产生真正的随机数,因此在概率算法中使用的随机数都是一定程度上随机的,即伪随机数。
线性同余法是产生伪随机数的最常用的方法。由线性同余法产生的随机序列a0, a1, …, an满足

其中,b≥0,c≥0,m>0,d≤m。d称为该随机序列的种子。如何选取该方法中的常数b、c和m直接关系到所产生的随机序列的随机性能。这是随机性理论研究的内容,已超出本书讨论的范围。从直观上看,m应取得充分大,因此可取m为机器大数,另外应取gcd(m,b)=1,因此可取b为一素数。
统计模拟——蒙特卡罗算法数值概率算法
一、 用随机投点法计算π值
设有一半径为r的圆及其外切四边形。向该正方形随机地投掷n个点。设落入圆内的点数为k。由于所投入的点在正方形上均匀分布,因而所投入的点落入圆内的概率为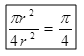
。所以当n足够大![]()
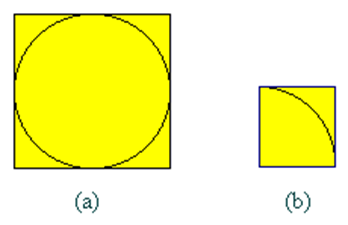
算法如下:
main( )
{long total,inside,i; float x,y;
input (total); inside=0;
for(i=1;i<= total;i++)
{ x= fRandom(0,1); y= fRandom(0,1);
if (x*x+y*y<=1) inside=inside+1; }
print(4*inside/total);
}
计算定积分

算法如下:
main( )
{long total,inside,i; float x,y;
input (total); // 读入要产生的随机点的数目
inside=0;
for(i=1;i<= total;i++)
{ x= fRandom(0,1); y= fRandom(0,1);
if (y<=f(x)) // 可以事先编写函数f(x)
inside=inside+1; }
print(inside/total);
}
考虑正确几率的算法—蒙特卡罗(Monte Carlo)算法
就像天气预报一样,有些软件的功能不能达到百分之百的正确率,如自动翻译系统、机器问答系统等,蒙特卡罗算法可以在模拟中“在一般情况下保证对问题的所有实例都以高概率给出正确解”的算法,但是,算法通常无法判定一个具体解是否正确。
蒙特卡罗(MC)算法的相关术语和结论如下:
(1)p正确(p-correct):设如果一个MC算法对于问题的任一实例得到正确解的概率不小于p,p是一个实数,且1/2≤p<1。且称p-1/2是该算法的优势(advantage)。
(2)一致的(consistent):如果对于同一实例,蒙特卡罗算法不会给出2个不同的正确解答。
(3)偏真(true-biased)算法:当MC是求解判定问题的算法,算法MC返回true时解总是正确的,当它返回false不一定正确。反之称为偏假(flase-biased)算法。
(4)偏y0算法(y0-biased):更一般的情况,所讨论的问题不一定是一个判定问题,一个算法MC是偏y0的算法(y0是某个特定解),即如果存在问题实例的子集X使得:
当xX时,则算法MC(x)返回的解总是正确的(无论返回y0还是非y0);
当xX时,正确解是y0,但MC并非对所有这样的实例x都返回正确解y0。
(5)重复调用一个一致的,p正确偏y0蒙特卡罗算法k次,可得到一个(1-(1-p)k)正确的蒙特卡罗算法,且所得算法仍是一个一致的偏y0蒙特卡罗算法。
【例4】素数测试:判断给定整数是否为素数。
算法设计1:至今没有发现素数的解析式表示方法,判定一个给定的整数是否为素数一般通过枚举算法来完成:
int prime(int n)
{ for (i=2; i <=n-1; i++)
if (n mod i= =0) return 0;
return 1; }
算法的时间复杂性是O(n),可以缩小枚举范围为2- n 1/2,算法的时间复杂性是O(n 1/2)。但对于一个m位正整数n,算法的时间复杂性仍是O(10m/2),也就是说这个算法的时间复杂性关于位数是指数阶的。
算法设计2:简单的随机算法,随机选择一个数,若是n的因数,则下结论n不是素数;否则下结论n是素数。
prime(int n)
{ d = Random(2,sqrt(n)); // 产生2-n 1/2的随机整数;
if (n mod d =0) return 0;
else return 1;
}
若返回0,则算法幸运地找到了n的一个非平凡因子,n为合数,算法完全正确,因此,这是一个偏假算法。若返回1,则未必是素数。实际上,若n是合数,prime 也可能以高概率返回1。
例如:n=61*43,prime在2~51内随机选一整数d
成功:d=43,算法返回false(概率为2%) ,结果正确
失败:d≠43,算法返回true(概率为98%),结果错误
当n增大时,情况更差。
和费尔马小定理一样,若方程x2≡1(mod n)的解不为x=1和n-1则说明n一定是合数;若方程x2≡1(mod n)的解为x=1和n-1并不能说明n一定是素数,但n是素数的概率非常高。
依据费尔马小定理和二次探测定理,对随机生成的数a, 计算an-1 mod n,并同时实施对n的二次探测,二次探测的序列为a2,(a2 mod n)2,……。这样可以更高概率地保证算法的正确性。
算法如下:
power(int a, int b, int n)
{ int y=1,m=n,z=a;
while(m>0) //计算an-1 mod n
{ while(m mod 2=0)
{int x=z; z=z*z mod n; m=m/2;
if ((z=1) and (x<>1) and (x<>n-1)) // n为合数
return 1;
}
m--;
y=y*z mod n;
}
if (y=1) return 0; //n高概率为素数
return 1; //n为合数
}
prime(unsigned int n) // 素数测试的蒙特卡罗算法
{ int i,a, q=n-1;
for(i=1;i<log(n);i++)
{a=Random(2,n-1);
if(power(a,n-1,n) return 0; // n为合数
}
return 1; //n高概率为素数
}
随机序列提高算法的平均复杂度 ——舍伍德(Sherwood)算法
算法的平均时间复杂度主要依赖数据的规模,其次很多算法还依赖于数据的初始状态,典型的有插入排序、快速排序和搜索算法等都是如此。特别是快速排序,平均时间复杂度为O(nlogn),但在数据基本有序时最坏时间复杂度为O(n2)。舍伍德算法的思想就是应用随机序列提高算法的平均时间复杂度。
【例1】快速排序改进。
快速排序中利用随机序列选取枢轴值,可以提高快速排序的平均效率,避免最差情况的出现。
快速排序算法的关键在于一次划分中选择合适的轴值作为划分的基准,如果轴值是序列中最小(或最大)记录时,则一次划分后,由轴值分割得到的两个子序列不均衡,使得快速排序的时间性能降低。
舍伍德型概率算法在一次划分之前,根据随机数在待划分序列中随机确定一个记录作为轴值,并把它与第一个记录交换,则一次划分后得到期望均衡的两个子序列,从而使算法的行为不受待排序序列初始状态的影响,使快速排序在最坏情况下的时间性能趋近于平均情况的时间性能。
随机快速排序算法如下:
void QuickSort (int r[ ], int low, int high)
{
if (low<high) {
i=Random(low, high);
r[low]←→r[i];
k=Partition(r, low, high);
QuickSort(r, low, k-1);
QuickSort(r, k+1, high);
}
}
如果一个算法无法直接利用随机序列改造成舍伍德算法,则可借助于随机预处理技术,即不改变原有的算法,仅对其输入实例进行随机排列(称为洗牌)。假设输入实例为整型,下面的随机洗牌算法可在线性时间实现对输入实例的随机排列。
【例2】随机洗牌算法
void RandomShuffle(int n, int r[ ])
{ for (i=0; i<n; i++)
{ j=Random(0, n-i-1);
swap(r[i], r[j]); //交换r[i], r[j]
}
}
随机生成答案并检测答案正确性 ——拉斯维加斯(Las Vegas)算法
现实中很多问题及其解无规律可言,无法使用递推、贪婪法、分治法或动态规划法解决,只能通过蛮力法来解决,也就是把所有可能的结果列举出来,逐一判断那个是正确结果。这种算法无论利用循环还是递归机制进行枚举,只能按一定规律从小到大或从大到小枚举,而问题的答案一般是中间的数据,这样,算法的效率往往较低。拉斯维加斯算法的思想是用随机序列代替有规律的枚举,然后判断随机枚举结果是否问题的正确解。此方法在不需要全部解时,一般可以快速找到一个答案;当然也有可能在限定的随机枚举次数下找不到问题的解,只要这种情况出现的概率不占多数,就认为拉斯维加斯算法是可行的。当出现失败情况时,还可以再次运行概率算法,就又有成功的可能。
【例1】n皇后问题的改进
问题分析:对于n皇后问题的任何一个解而言,每一个皇后在棋盘上的位置无任何规律,不具有系统性,而更象是随机放置的。由此容易想到下面的拉斯维加斯算法。
算法设计:在棋盘上的各行随机地放置皇后,并注意使新放置的皇后与已放置的皇后互不攻击,当n个皇后均已相容地放置好,或已没有下一个皇后的可放置位置时为止。直到找到一解或尝试次数大于1000次,算法结束。
数据结构设计:用数组元素try[1]-try[8]存放结果,try[i]——表示第i个皇后放在(i,try[i])位置上。
算法如下:
void Queens()
{ int try[8]={0}, success=0, n=0;
while (!success and n<1000)
{ success=LV(try);n++}
if( success) for(i=1;i<=8;i++) print(try[i]);
else print(“not find”);}
Lv (int try[])
{ for(i=1;i<=8;i++)
{try[i]=Random(1,8); if( !check(try,i)) return 0; }
return 1;}
check(int a[ ],int n)
{ for (int i=1;i<=n-1;i=i+1)
if (abs(a[i]-a[n])=abs(i-n)) or (a[i]=a[n])
return(0);
return(1); }
【例2】求因子问题:设n>1是一个整数。若n是合数,则n必有一个非平凡因子x(不是1和n本身)。给定合数n,求n的一个因子。
算法设计1:
一个数的因子没有统一的规律,只能通过枚举算法来枚举可能的因子,算法如下:
int Split(int n)
{ int m.i;
m =sqrt(n); // sqrt(n)为开方函数
for (i=2; i<=m; i++)
if (n mod i==0) return i;
return 1;
}
算法设计2:
利用拉斯维加斯算法的思想,在开始时选取0~n-1范围内的随机数x1,然后用xi=(xi-12-1)mod n递推产生无穷序列x1, x2, …, xk, …
对于i=2k,以及2k<j≤2k+1,算法计算出xi-xj与n的最大公因子d=gcd( xi-xj ,n)。如果d是n的非平凡因子,则算法输出n的因子d。
int Pollard(int n)
{ int i=1,x,y,d; print(n, ”=”);
x= Random(0,n-1); // 随机整数
y=x, k=2;
while (1)
{i++; x=(x*x-1)mod n; // 求n的非平凡因子
d= gcd (y-x , n); // gcd(a , b)求a , b 的最大公因子
if ((d>1) && (d<n)) return d;
if (i==k) {y=x; k*=2;}
}