最近在学习深度学习，其中涉及到参数优化的算法，其中就有梯度下降算法，笔者不想浅尝辄止，认为很有必要了解下相关的数学知识，总结了下有关梯度的相关数学知识。
导数
一张图读懂导数与微分：
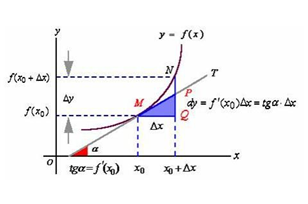
这是高数中的一张经典图，如果忘记了导数微分的概念，基本看着这张图就能全部想起来。
导数定义如下：
定义：设函数y=f(x)在点x0的某个领域内有定义，如果Δy/Δx在当Δx→0时极限存在，则称函数y=f(x)在x0处可导，这个极限是函数y=f(x)在x0处的导数
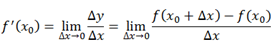
反映的是函数y=f(x)在某一点处沿x轴正方向的变化率。再强调一遍，是函数f(x)在x轴上某一点处沿着x轴正方向的变化率(变化趋势)。直观地看，也就是在x轴上某一点处，如果f’(x)>0，说明f(x)的函数值在x点沿x轴正方向是趋于增加的；如果f′(x)<0，说明f(x)的函数值在x点沿x轴正方向是趋于减少的。
这里补充上图中的Δy、dy等符号的意义及关系如下：
Δx：x的变化量；
dx：x的变化量Δx趋于0时，则记作微元dx；
Δy：Δy=f(x0+Δx)-f(x0)，是函数的增量；
dy：dy=f’(x0)dx，是切线的增量；
当Δx→0时，dy与Δy都是无穷小，dy是Δy的主部，即Δy=dy+o(Δx).
导数与导函数的关系是局部与整体的关系，导数通常是指一点，导函数则是指一个区间上的
微分：
定义：设函数y=f(x)在某个领域内有定义，x0及x0+Δx在这区间内，如果增量
高阶无穷小的定义：如果lim α/β=0，就说β是比α高阶的无穷小，记作β=o(α)
偏导数
一元函数的变化率是导数，多元函数的自变量有多个，当某个自变量x变化而其它自变量固定时，这时候对变化的自变量x进行求导，就称为多元函数对于x的偏导数。
定义：设函数z=f(x,y)在点(x0,y0)的某一领域内有定义，当y固定于y0，而x在x0处有增量Δx，相应的函数有增量
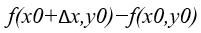
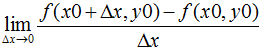
存在，则称该极限为z=f(x,y)在点(x0,y0)处对x的偏导数
偏导数的几何意义
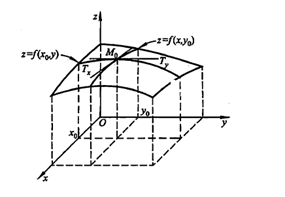
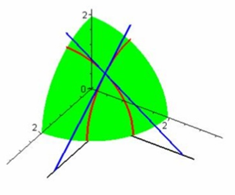
偏导数fx(x0,y0)就是曲面被平面y=y0所截得的曲线在点M0处的切线M0Tx对x轴的斜率
偏导数fy(x0,y0)就是曲面被平面x=x0所截得的曲线在点M0处的切线M0Ty对y轴的斜率
从以上二元函数的偏导数推广到多元函数的偏导数如下所示：
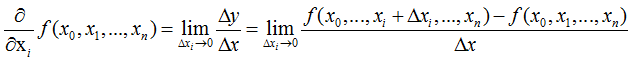
可以看到，偏导数与导数的本质是一致的，都是当自变量的变化量趋于0时，函数值的变化量与自变量变化量比值的极限。直观地说，偏导数也就是函数在某一点上沿某一分量（坐标轴）正方向的的变化率。
全微分：
参考上文微分的定义，与一元函数的情形一样，希望用自变量增量Δx,Δy来线性函数来代替函数的全增量Δz，从而减化计算
定义：设函数z=f(x,y)在点(x,y)的某领域内有定义如果函数在点(x,y)的全增量
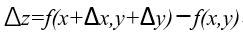
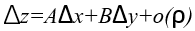
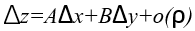，则称函数z=f(x,y)在点(x,y)处
可微分，而AΔx+BΔy称为函数在点(x,y)的全微分, dz=AΔx+BΔy
可微分与偏导数的关系
基于上述全微分定义成立，存在某一点p′(x+Δx,y+Δy)对于式子Δz=AΔx+BΔy+o(ρ)也成立，当Δy=0时
f(Δx+x,y)−f(x,y)=AΔX+o(|Δx|)
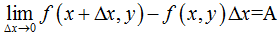
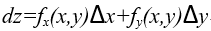
如果函数的各个偏数在点(x,y)是连续的，则函数可微分
方向导数
导数、偏导数、方向导数定义都是说如果说某条件下极限存在，谨记导数的本质是极限及代表函数的变化率，偏导数反映的是函数沿坐标轴方向的变化率，有所限制。所以引入方向导数表示沿任意一方向的变化率。
定义：设l是xOy平面以P0(x0,y0)为始点的一条射线，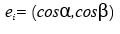
是以射线同方向的单位向量
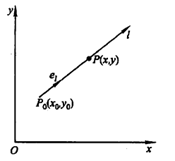
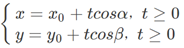
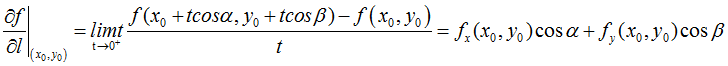
更一般的，对于多元函数在方向l(ΔX0,ΔX1,… ,ΔXn)上的方向导数为
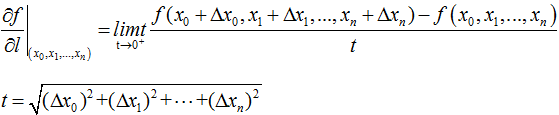
方向导数与全微分的关系
由全微分的定义得到
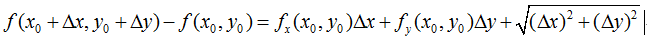
设点 在以 为起点、长度为t的射线l(cosα,cosβ)上，则有Δx=tcosα,Δy=tcosβ, ，所以
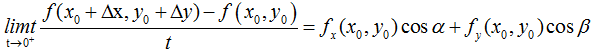
上式左侧就是方向导数定义形式，极限存在即方向导数存在，且其值等于右式
由此得到定理，如果函数 f(x,y) 在点 P0(x0,y0) 可微分,那么函数在该点沿任一方向l的方向导数存在
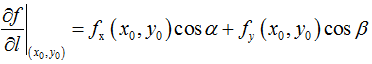
梯度
在平面上确定某一点可能存在无数个方向导数，我们怎样找到其中一个方向导数来描述函数最大变化率？
定义：在二元函数的情形，设函数f(x,y)在平面区域D内具有一阶连续偏导数，对于每一点P0(x0,y0)∈D，都可以给出一个向量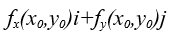
或用坐标表示
其中i, j为x,y轴的方向向量，上述微量称为函数f(x,y)在点P0(x0,y0)的梯度记作
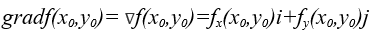
对于多元函数有：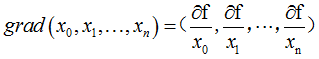
,再次强调：梯度是一个向量。
由定义看到，梯度的方向是确定的，如果点P的坐标确定，那么梯度也大小也确定
如果函数f(x,y)在点P0(x0,y0)可微分，el=(cosα,cosβ)是方向l的方向向量(方向未确定)
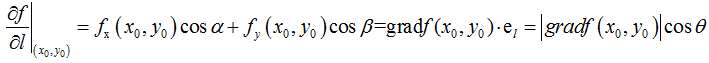
其中θ为向量grad f(x0,y0)与向量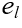
的夹角
这一关系式表明了函数在一点的梯度与函数在这点的方向导数间的关系。特别的由这个关系可知：
（1）当θ=0时，即方向el与梯度grad f(x0,y0)的方向相同时，函数f(x,y)增加最快，函数在这个方向的方向导数达到最大值，由上式容易看出，这个值就是梯度grad f(x0,y0)的模，即
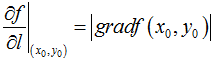
（2）当θ=π时，即方向el与梯度grad f(x0,y0)的方向相反时，函数f(x,y)减小最快，函数在这个方向的方向导数达到最小值，即
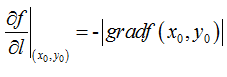
（3）当θ=π/2时，即方向el与梯度grad f(x0,y0)的方向正交时，函数f(x,y)的变化率为0，即
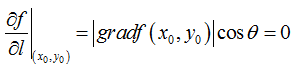
所以可以用沿梯度方向的方向导数来描述是函数最大变化率，即梯度方向是函数变化率最大的方向，在梯度定义的时候就已经赋予了它这个特性。
为什么梯度的方向与等高线切线方向垂直