作者:石川
链接:https://zhuanlan.zhihu.com/p/38276041
来源:知乎
已获得作者同意转载。
1 前言
移动平均(Moving Average,MA),又称移动平均线,简称均线。作为技术分析中一种分析时间序列的常用工具,常被应用于股票价格序列。移动平均可过滤高频噪声,反映出中长期低频趋势,辅助投资者做出投资判断。
根据计算方法的不同,流行的移动平均包括简单移动平均、加权移动平均、指数移动平均,更高阶的移动平均算法则有分形自适应移动平均、赫尔移动平均等。这其中,简单移动平均又最为常见。下图为上证指数日线的 5 个不同计算窗口(20 日,50 日,120 日,200 日,300 日)的简单移动平均线。
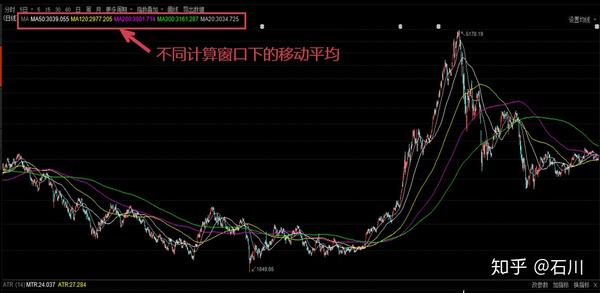
简单移动平均(Simple Moving Average, SMA)就是对时间序列直接求等权重均值,因此使用简单。但其最令人诟病的就是它的滞后性。从上图不难看出,随着计算窗口 的增大,移动平均线越来越平滑,但同时也越来越滞后。以 120 日均线为例,在 2015 年 6 月份之后的大熊市开始了很长一段时间之后,120 日均线才开始呈现下降趋势。如果我们按照这个趋势进行投资,那这个滞后无疑造成了巨额的亏损。
事实上,任何移动平均算法都会呈现一定的滞后性。它以滞后性的代价换来了平滑性,移动平均必须在平滑性和滞后性之间取舍。然而,滞后性是怎么产生的呢?简单移动平均在时间上滞后多少呢?有没有什么高级的移动平均算法能在保证平滑性的同时将滞后性减小到最低呢?这些就是本文要回答的问题。
2 移动平均的本质
移动平均的本质是一种低通滤波。它的目的是过滤掉时间序列中的高频扰动,保留有用的低频趋势。如何从时间序列中抽取出真正的低频趋势呢?无论采取哪种移动平均算法,理论上的计算方法都相同,下面我们简要说明。同时,我们也会清晰地阐述该计算方法仅在理论上有效,而在实际应用中是无法实现的,并由此揭示产生滞后性的原因。
假设我们有一个时间序列 ,如下图所示。另外,假设我们有一个作用在时域 t 上的过滤函数 F(注:这个 F 的具体形式根据不同的移动平均算法而不同)。
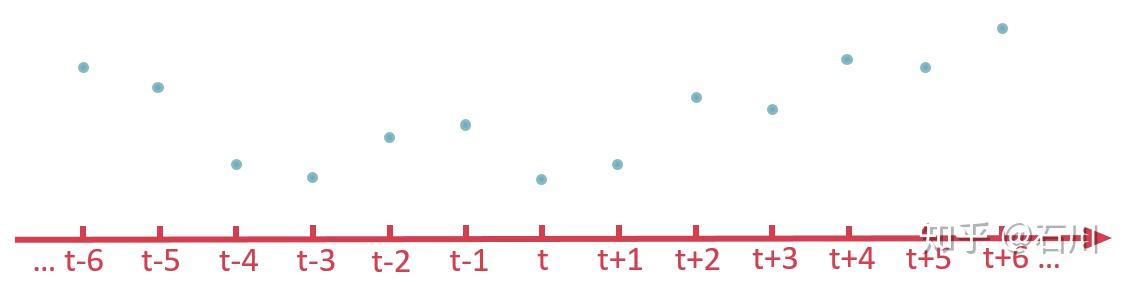
在理论上,在任意 时刻的低频滤波(用
表示)在数学上可以表示为该时间序列
和过滤函数
在整个时域上的卷积,即
其中, 为过滤函数
在时刻
的取值。由于在实际中不可能用到无穷多的数据,因此可以考虑给过滤加一个窗函数,即过滤函数
只在窗口长度
内有效、在窗口之外为 0,如下图所示:
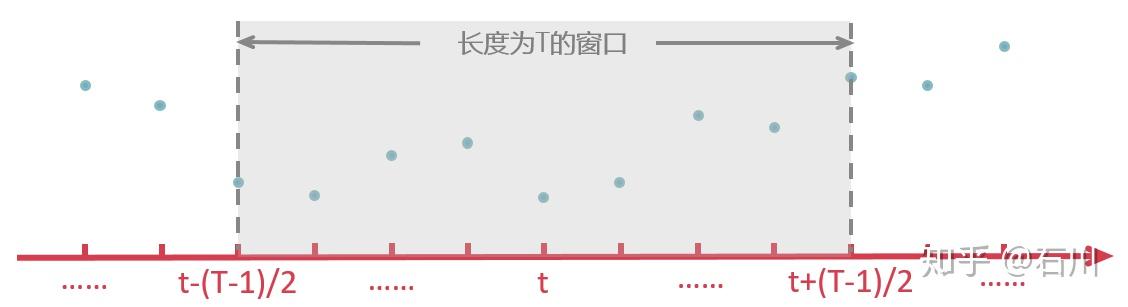
加入长度为 的窗函数后,在时刻t的低频滤波变为该时间序列
和过滤函数
在这个窗口内的卷积:
然而,无论是否使用加窗函数,上述公式最大的问题是,在计算 时刻的低频分量时,利用到了未来的数据。换句话说,理论上的低通滤波(或者移动平滑)必须要用事后数据,其假设所有数据都发生后再在全局上计算所有时点的低频分量。但这在实时数据中是不可能的,因为在任何当前时刻
,我们都没有未来数据可以利用。
正因如此,在实际应用中,我们无法使用 到
之间的数据,只能退而求其次使用
到
之间的数据。这相当于我们把计算低频趋势的过滤窗函数在时域上向左平移
个单位,如下图所示:
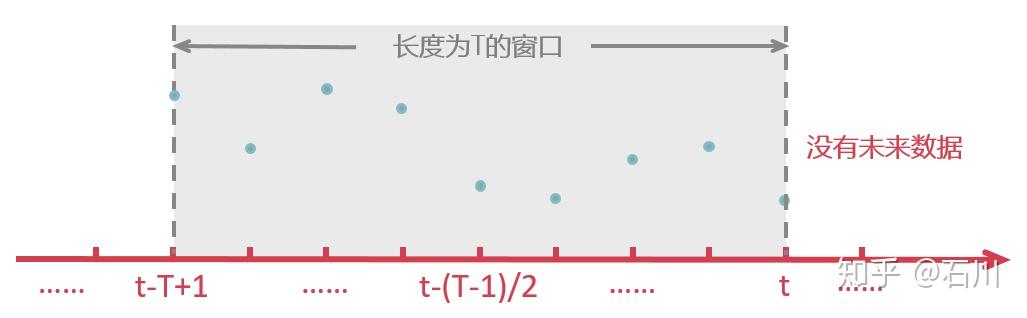
如此处理后,对于实时数据,在当前时刻 的低频滤波变为该时间序列
和过滤函数
在
到
之间的卷积:
没有未来数据便是滞后的根本原因。
对于简单移动平均来说,在窗口 内,过滤函数在每个时点的取值都是
。利用上述公式计算得到的实际上是
时刻(而非
时刻)的低频趋势,而我们把它当作
时刻的低频趋势使用,这便产生了
的滞后。当我们使用简单移动平均时,在当前时刻
,对于给定的时间窗口
,我们仅能求出
时刻之前的低频趋势,而无法求出
之后的低频趋势。这也解释了为什么时间窗口
越大,滞后
越多。这就是为什么看股票数据里面 MA20、MA30、MA50 等日均线这种,计算均线的窗口
越大,得到的移动平滑曲线越滞后。
既然无论如何都没有未来数据,那么是否意味着我们就只能接受移动平均的滞后性呢?答案是否定的。换个角度来考虑这个问题,滞后性说明由简单移动平均计算得到的低频趋势对近期的最新数据不够敏感。这是由于它在计算低频趋势时,对窗口内所有的数据点都给予相同的权重。按着这个思路延伸,自然的想法就是在计算移动平均时,给近期的数据更高的权重,而给窗口内较远的数据更低的权重,以更快的捕捉近期的变化。由此便得到了加权移动平均和指数移动平均。
3 加权移动平均
在计算加权移动平均(Weighted Moving Average, WMA)时,窗口内的过滤函数的取值从当前数据到之前第 期的数据依次线性递减。因此,第
期的
为
。该权重是
的单调线性递减函数。下图为
时不同
的取值对应的权重(图片来自 wiki)。
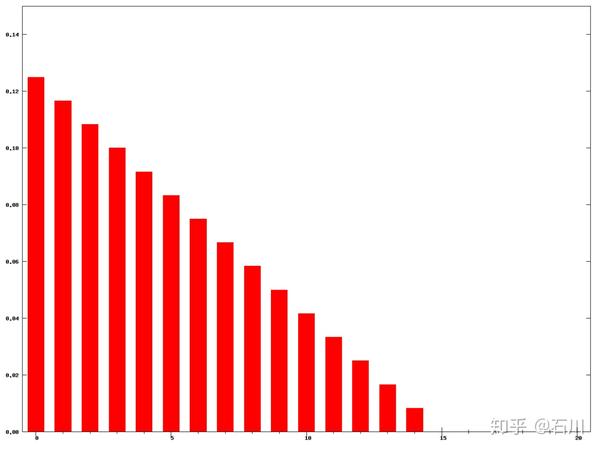
在确定了权重后, 时刻的加权移动平均(记为
)由下式得到:
值得一提的是,由于严格的按照线性递减,因此权重会最终在当前时刻之前的第 期时点衰减为 0。
以上证指数过去 10 年的日数据为例,下图比较了 时的简单移动平均和加权移动平均的过滤效果。加权移动平均比简单移动平均对近期的变化更加敏感,尤其是在牛熊市转换的时候,加权移动平均的滞后性小于简单移动平均。但是,由于仅采用线性权重衰减,加权移动平均仍然呈现出滞后性。
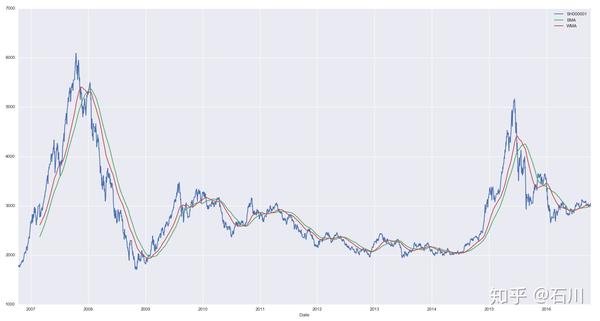
4 指数移动平均
指数移动平均(Exponential Moving Average, EMA)和加权移动平均类似,但不同之处是各数值的加权按指数递减,而非线性递减。此外,在指数衰减中,无论往前看多远的数据,该期数据的系数都不会衰减到 0,而仅仅是向 0 逼近。因此,指数移动平均实际上是一个无穷级数,即无论多久远的数据都会在计算当期的指数移动平均数值时有一定的作用,只不过离当前太远的数据权重非非常低,因此它们的作用往往可以忽略。
在实际应用中, 时刻的指数移动平均(记为
)可以按如下方法得到:
其中 表示权重的衰减程度,取值在 0 和 1 之间。
越大,过去的观测值衰减的越快。虽然指数移动平均是一个无穷级数,但在实际应用时,我们也经常看到
期指数移动平均的说法。这里的
是用来计算
的参数,它不表示指数衰减在 T 期后结束。
和
的关系为
。下图为
时不同时刻的权重(图片来自 wiki)。可以看到,任何一期的权重都不会衰减到 0。
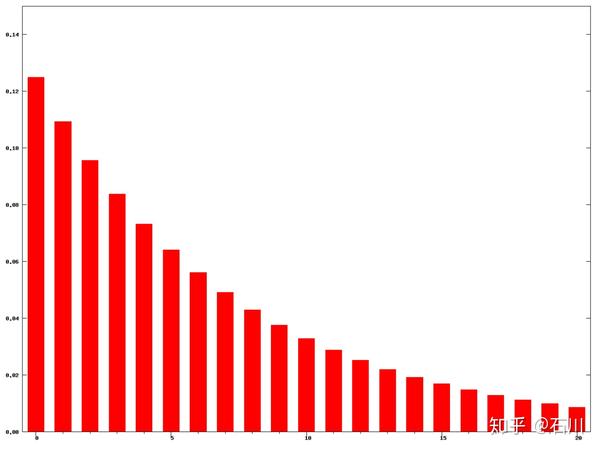
下图比较了 时简单移动平均、加权移动平均和指数移动平均的平滑效果。指数移动平均由于对近期的数据赋予了更高的权重,因此它比加权移动平均对近期的变化更加敏感,但这种效果在本例中并不显著,指数移动平均也存在一定的滞后。
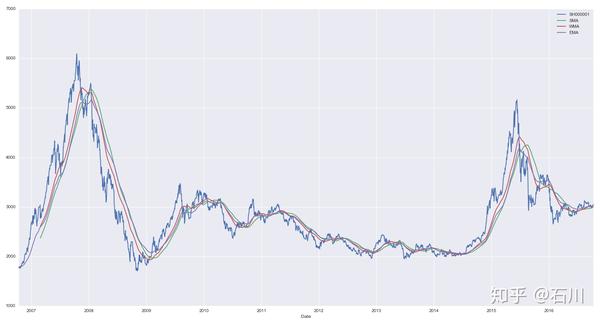
当 时,得到的指数移动平均又称为修正移动平均(Modified Moving Average,MMA)或平滑移动平均(SMoothed Moving Average,SMMA),它们在应用中也十分常见。比如,在计算技术指标 ADX 的时候,就应用到了平滑移动平均。
无论是加权还是指数移动平均,它们都是通过对近期的数值赋予更高的权重来提高低频趋势对近期变化的敏感程度。然而,它们的计算表达式(或算法结构)是固定的,在整个时间序列上的各个时点都使用同样的结构(即一成不变的权重分配方法)计算移动平均,而不考虑时间序列自身的特点。
一个优秀的移动平均算法计算出来的均线应在时间序列自身波动不明显的时点足够平滑,而在时间序列自身发生巨变时迅速捕捉、将滞后最小化。要想达到这种效果,就必须利用时间序列自身的特点。分形自适应移动平均算法就是这样一个有力的工具。
5 分形自适应移动平均
顾名思义,分形自适应移动平均(FRactal Adaptive Moving Average,FRAMA)利用了投资品价格序列的分形特征。简单的说,该算法通过一个简单的公式计算从时间序列从当前时点往前 长度的时间窗口内的分形维数
,并利用分形维数进一步求解指数移动平均的参数
。
分形维数描述时间序列的趋势,其取值在 1 到 2 之间,越大说明趋势越明显,越小说明时间序列越随机。因此,通过连续的计算时间序列局部的分形维数,该算法可以动态的、自适应的根据时间序列的特征计算平滑所用的参数。由于 是
的减函数,因此
越大(趋势越明显),
越小,即指数平滑时对过去的数值衰减的越慢;
越小(随机性越强),
越大,即指数平滑时对过去的数值衰减的越快、对最新数据的变化越敏感。
具体的,对于当前时点 和给定的窗口
,该方法用到了三个时间窗口,即
到
(记为窗口
,长度为
),
到
(记为窗口
,长度为
),以及
到
(记为窗口
,长度为
)。不难看出,
。该方法的步骤如下:
计算 FRAMA 均线的步骤:
- 用窗口
内的最高价和最低价计算
- 用窗口
内的最高价和最低价计算
- 用窗口
内的最高价和最低价计算
- 计算分形维数
- 计算指数移动平均的参数
,并使其满足在 0.01 和 1 之间
- 将
带入指数移动平均的公式求解
时刻的 FRAMA 移动平均值
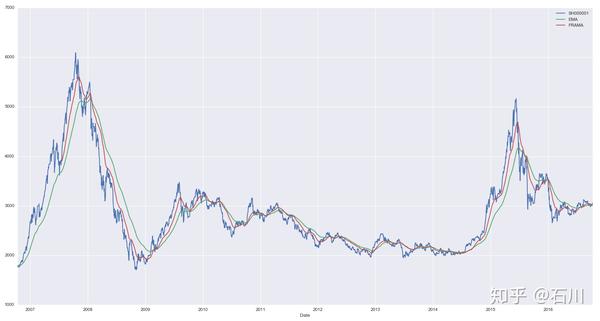
下图比较了 时指数移动平均以及分形自适应移动平均的平滑效果。很明显,由于利用了时间序列自身的分形特征,FRAMA 均线对滞后性的提高非常明显,这意味着在价格趋势发生变化的时候它捕捉的更加及时。当然,取决于选取的参数,FRAMA 均线在一些局部可能不够平滑,它体现了一种动态的对平滑度和灵敏度的取舍。
6 赫尔移动平均
最后,我们再介绍一种业界常用的高级移动平均算法,即赫尔移动平均(Hull Moving Average,HMA)。它由 Alan Hull 发明,故由此得名。该算法最大的特点是在减少滞后的同时有效的提高了均线的平滑程度。
在本文中,我们并不对它背后的逻辑做太多的剖析,这将留到今后介绍。我们直接给出它的计算步骤。对于给定的窗口 :
计算 HMA 均线的步骤:
- 计算窗口为
的加权移动平均,并把结果乘以 2(如果
不是整数则取整)
- 计算窗口为
的加权移动平均
- 用第 1 步的结果减去第 2 部的结果,得到一个新的时间序列
- 以第 3 步得到的时间序列为对象,计算窗口为
,的加权移动平均(如果
不是整数则取整)
上述步骤的数学表达式为 。
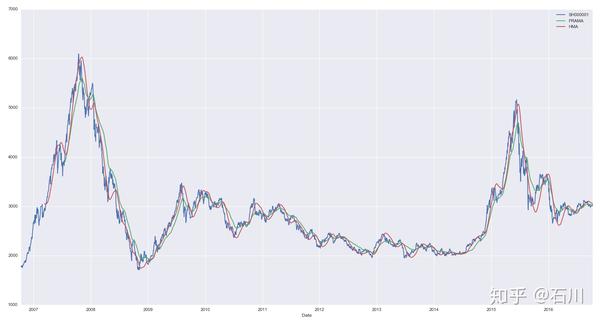
最后,比较 时分形自适应移动平均和赫尔移动平均的平滑效果。令人惊喜的看到,HMA 均线有着不输 FRAMA 均线的灵敏性(滞后性非常低),并且在局部也提高了平滑性,确实做到了在保证平滑性的同时最大的降低了滞后性。
7 结语
作为技术分析的利器,移动平均线人人都在看、人人都在用。可又有多少人想得清楚、用的明白呢?本文详尽的分析了移动平均技术的本质,揭示了滞后性产生的原因。通过对五种不同过滤技术的分析和对比,说明了高级的移动平均技术(比如 FRAMA 和 HMA)可以有效的降低滞后性并保证均线的平滑性。