前置知识
矩阵、求导
知识地图
学习一个新事物之前,先问两个问题,我在哪里?我要去哪里?这两个问题可以避免我们迷失在知识的海洋里,所以在开始之前先看看地图。
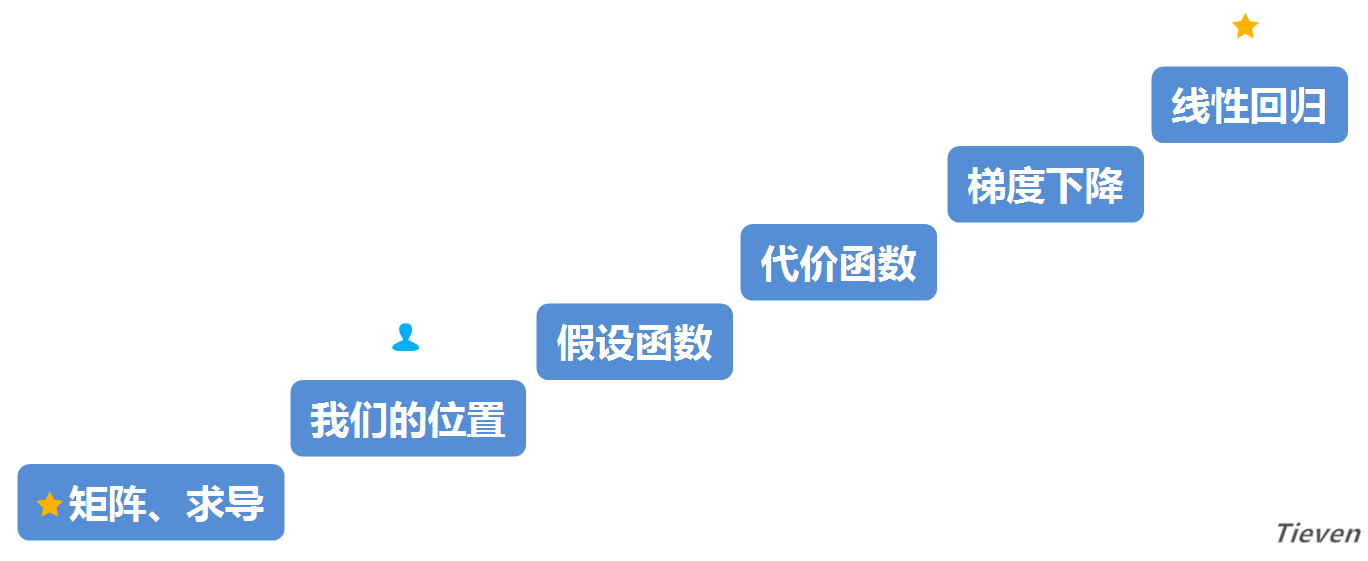
此前我们已经为了解线性回归做了一点准备工作,现在开始正式进入主题,总共需要迈过三个台阶。希望文章结束的时候,我们能轻松愉悦地摘下这颗星星。
从一个例子开始
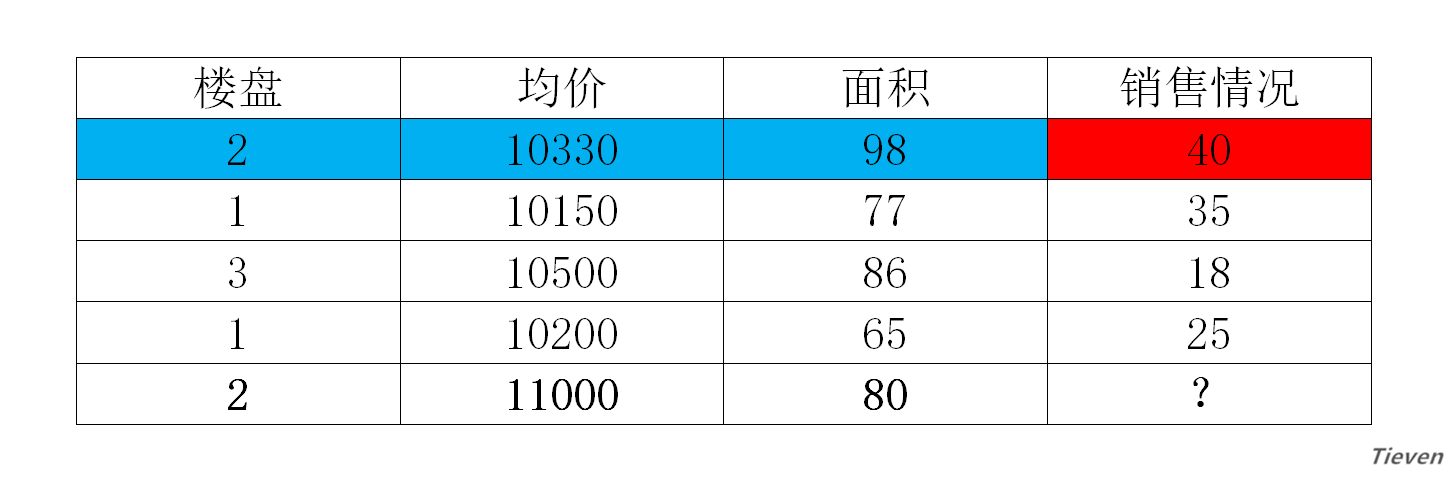
假设我们是市场营销人员,现在有一些房屋历史销售数据,这些数据中包含了房屋的楼盘、均价、面积,以及对应的房屋销售情况。现在有一个新开楼盘,已知新开楼盘的主要信息,如何预测楼盘的销售情况呢?
在这个问题中,我们称蓝色部分为样本,红色部分为结果。样本中包含若干种已知的数据特征,如楼盘,均价和面积。线性回归要解决的问题,就是给定一个样本的数据特征,来预测一个结果。
为了方便讨论和计算,通常将数据转换为向量和矩阵的形式,上面的问题可以转换为以下形式。

线性回归是通过对旧样本进行学习来预测新样本,所以在学习完成之前先不考虑新样本的情况,先把新样本扔掉。
左边是一个由样本构成的矩阵,通常约定用X表示;
右边是一个由结果构成的向量,通常约定用y表示;
矩阵中的每一列都是一个数据特征,在这个例子中有3个数据特征,所以有3列。矩阵中的每一行都是一个样本,在这个例子中有4个样本,所以有4行。
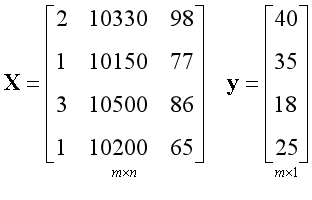
m和n是用来描述矩阵尺寸的符号。
m表示行的数量,对应样本的数量,在此例中m=4;
n表示列的数量,对应数据特征的数量,在此例中n=3;
什么是假设函数
线性回归所采用的模型是线性相关的,即假设结果是由不同的数据特征组成,每个数据特征占据一定的权重,权重用参数θ表示。数据特征与数据特征之间没有加减以外的运算。
假设函数的表示形式如下:
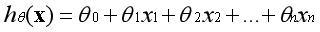
第一项可视为常数项,通常约定
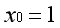
,则有:
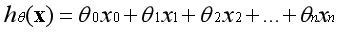
用向量的形式表示:

注:加粗的小写字母表示向量;
注:为了方便讨论,向量的下标从0开始计数,向量的长度为n+1;
用结构图的形式表示:
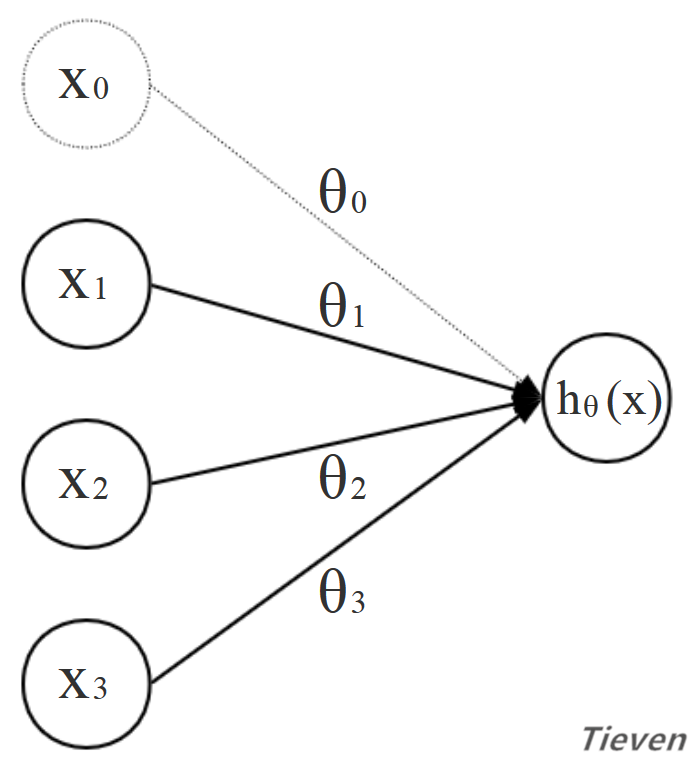
什么是代价函数
以一个数据特征为例,线性回归希望用直线尽可能地拟合样本,直观上看就是直线离样本间的距离足够近。如果直线离样本很远,说明线性回归的模型并不准确,因此可以用直线到样本间的距离作为评价模型好坏的标准。
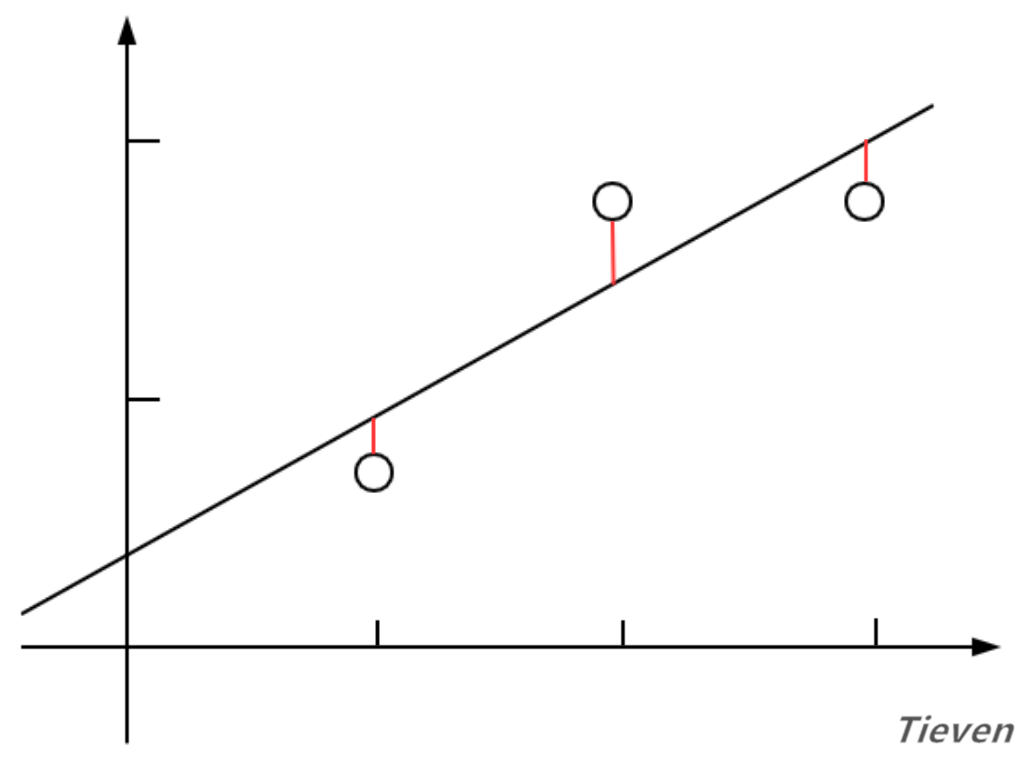
代价函数是衡量预测值和真实值之间的误差大小。当代价函数最小的时候,说明该模型最精确。代价函数的公式如下:
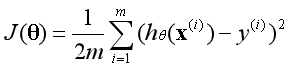
代价函数 = ((每个样本预测值与真实值的距离)的平方和)的均值
注:Σ是累加符号;
注:m表示样本的数量;
注:上标(i)表示第i个样本;
注:之所以前面的系数中多了一个1/2,是因为后续需要对代价函数求导,会出现系数2,两者相互抵消;
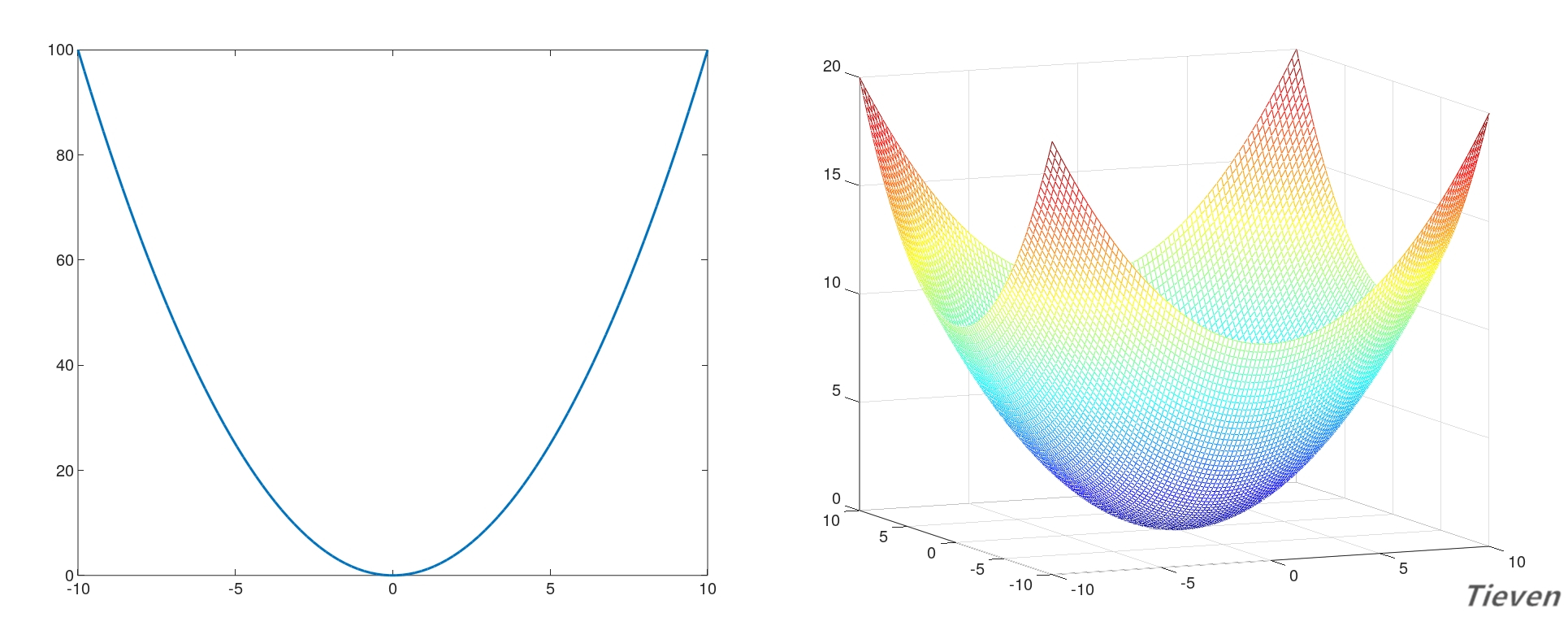
当有一个数据特征时,对应的有一个参数,代价函数如左图所示是一条二维空间中的曲线。
当有两个数据特征时,对应的有两个参数,代价函数如右图所示是一个三维空间中的曲面。
多个数据特征的代价函数无法可视化,然而通过观察可以发现,代价函数有一个最低点。当某一组参数对应的代价函数位于最低点时,就说明这组参数是最优解。
什么是代价函数的导数
如何求一个函数的最优解?对一个函数求导数,令导数为0,所得的解即为最优解。

如何求多变量函数的导数?

在代价函数中,参数θ是变量,对每一个变量θ求偏导时,将其他变量视为常数项。根据链式法则先对外层(蓝色部分)求导,然后对里层(橙色部分)求导。
如果这是一道数学题,我们可以令偏导数为0,通过联立方程组将每个偏导数直接求出来。但是在计算机上无法直接解出偏导数,需要通过一种叫梯度下降的方法来逐步得到最优解。
什么是梯度下降法
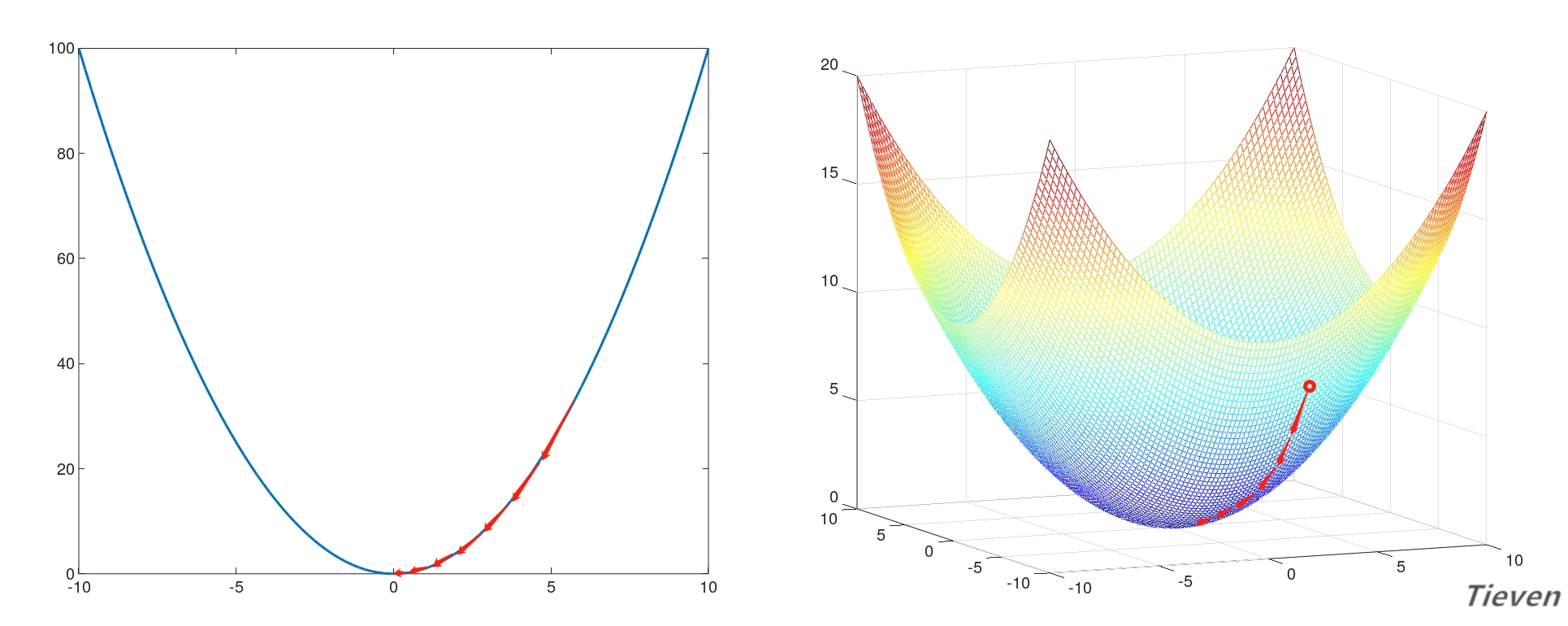
梯度下降法是让参数向偏导数的反方向调整,反复迭代,逐步靠近全局最优点的方法。如上图所示,从直观上看参数从任意一个位置出发,总是一步步接近最低的位置。
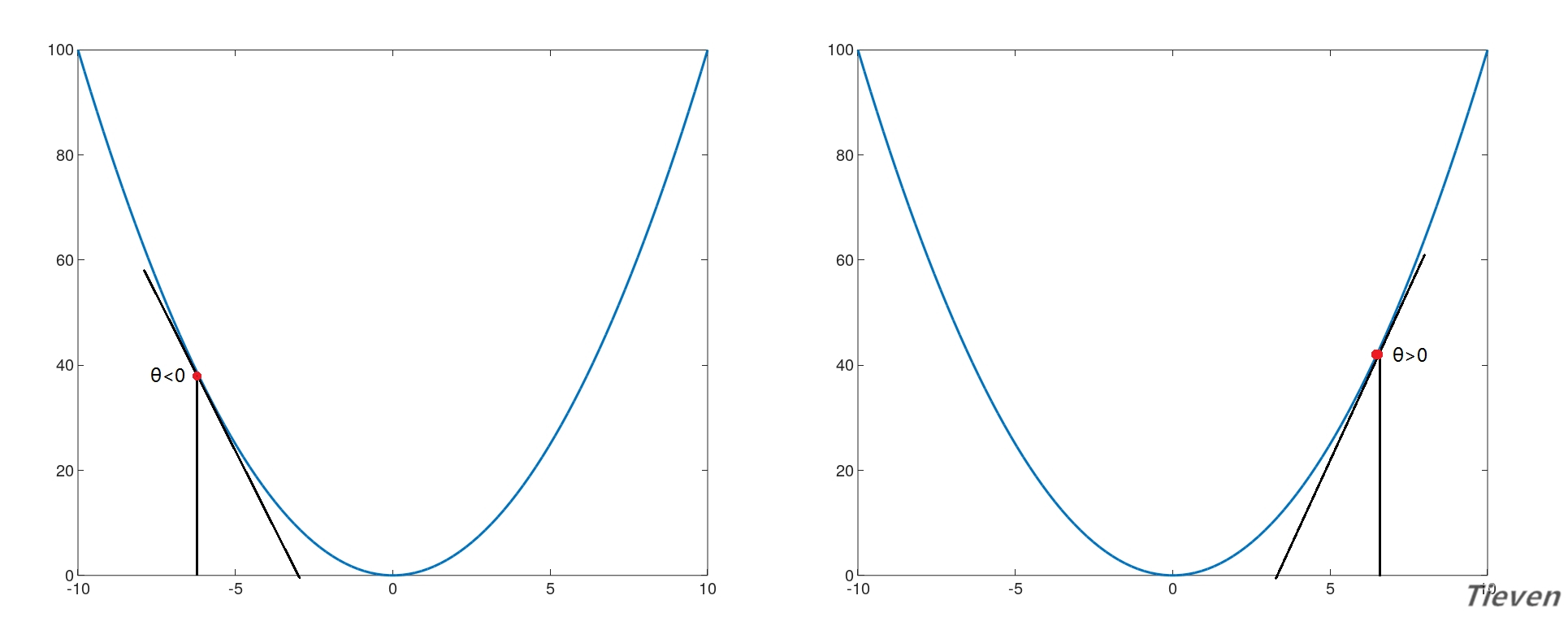
如右图所示,代价函数曲线右侧的斜率是正数,所以右侧的导数也是正数,如果想让参数往左移动,需要让参数减去偏导数(减去正数)。
如左图所示,代价函数曲线左侧的斜率是负数,所以左侧的导数也是负数,如果想让参数往右移动,需要让参数减去偏导数(减去负数)。
梯度下降公式(示例):

注:α为学习率;
注:n为特征的数量;
注意,在实际运用中,参数θ必须同时更新。一次梯度下降指的是所有的参数运用旧的参数同时更新一次。不能先更新第一个参数,然后用更新后的第一个参数去更新第二个参数。一次迭代的实际过程如下:
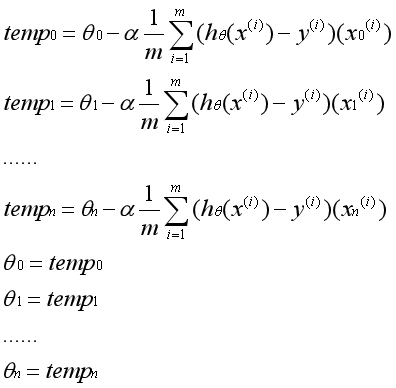
有n个数据特征就有n个梯度下降函数。一个点从任意的初始位置出发,通过梯度下降公式确定每个维度上的移动方向,综合起来即该点接下来的移动方向。反复迭代,最后到达全局最优点。
下图为两个正常运行的梯度下降的代价函数的图像:
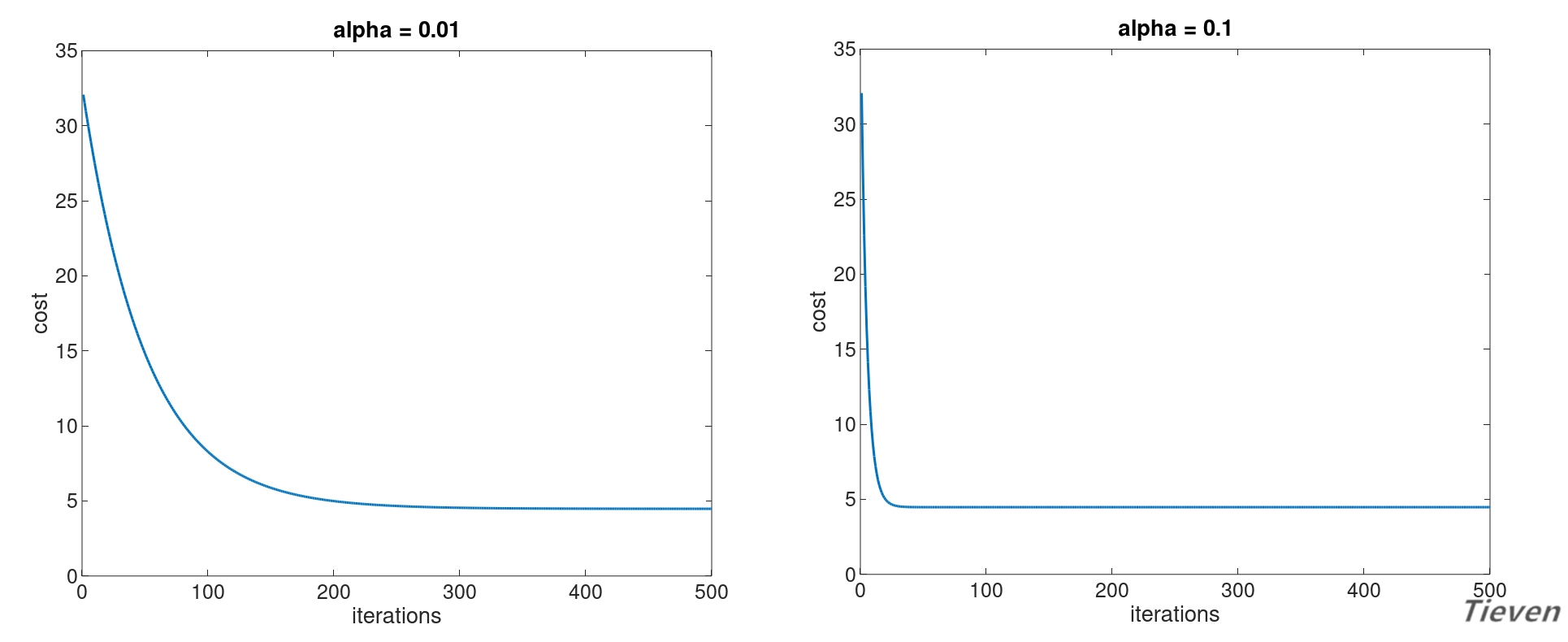
可以观察到随着迭代次数的增加,代价函数逐渐下降,说明参数在逐步逼近全局最优点。下降的速度是先快后慢,最后趋近于平行线,说明参数已经到达全局最优点。
与左边的梯度下降函数相比,右边的梯度下降函数收敛地更快了,只需要更少的迭代次数就可以将参数收敛到全局最优点,两者的差别在于学习率的设置不同。
什么是学习率
学习率是用来控制每次迭代中参数更新的幅度,这是一个需要手动设置的参数。

如左图所示,当学习率太小时,收敛速度慢,迭代次数多;
如右图所示,当学习率太大时,有可能不收敛,反而导致发散;
实际运用中通过手动调整尝试不同的学习率,具体的数值可以按照以下幅度进行尝试:0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1...
什么是特征缩放
影响梯度下降法收敛速度的第二个因素是不同特征的取值范围。原始数据的不同特征的取值范围可能差距很大,因此梯度下降法可能收敛地更加缓慢,同时也有更大的可能性会导致发散。
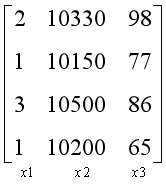
为了避免这种情况发生,可以通过特征缩放的方法,将不同特征的取值约束到一个相近的范围,这样梯度下降法就能更快地收敛。
一种特征缩放的方法,是将随机变量通过以下方法转换为均值为0,标准差为1的标准正态分布。
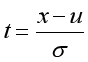
注:u表示均值
注:σ表示标准差

注意,在使用特征缩放以后,需要在第一列前加上全为1的一列,与常数项参数θ0相匹配。

什么是向量化(拓展)
涉及矩阵的运算,如果能实现向量化操作,就不需要使用循环语句。这样可以大幅度提高计算速度,即简洁又美观。通过一些线性代数上的变换,可以将梯度下降用一行代码表示。

注:X是样本构成的矩阵,矩阵规格为(m×n)
注:θ是参数构成的向量,向量规格为(n×1)
注:T表示矩阵的转置;
注:在说明原理时向量的下标是从0开始,在实际运用中向量的下标是从1开始;
总结
线性回归是用样本的预测值和真实值之间的距离来衡量模型的准确度,基于这一点构建出代价函数。要求代价函数的最优解,需要求出代价函数的偏导数,运用梯度下降法反复迭代,得到最终的参数θ。
理解了数学原理,下一步就是将其转化为代码的形式在计算机上进行实现,推荐使用Octave进行尝试,当然Python也是不错的选择。开头例子的答案是22.983。
至此我们能实现一个低配版的线性回归算法。而实际上有一种方法不需要学习率,不需要特征缩放,甚至不需要迭代,只需计算一次就可以得到答案。这将是我们AI之旅的下一站。
非正规代码

版权声明
1,本文为原创文章,未经作者授权禁止引用、复制、转载、摘编。
2,对于有上述行为者,作者将保留追究其法律责任的权利。
Tieven
2019.1.3