题目链接
题意:
题意是给定一个方阵的边长为2^n,然后给了一个k,然后询问,请问能不能从(1,1)->(n,n)路径保持方格的边长是相等的(这个路径是唯一的,是一个折线,从左下角到左上角,然后从左上角到右上角)
然后k是什么呢???
k是一个次数,操作是:把一个方格十字分解成四个同样大小的方格。
请问能否把这k次操作分配下去。如果可以输出YES,并且输出路径(边界格子的边长)
否则输出NO
题解:
参考博客,尊重原创(其中图是别人博客的,请尊重原作者,这是我偷窃别人的图)
这个题目有两个方面讨论,对于给定的数据范围来进行讨论。(其中是参考了运来哥和燕良兄的思路和做法)
1、观察n,k的两个数据的范围,不难看出来,其实这个n很大的时候k其实可以为任意值。
为什么有这样的想法呢???
首先我们需要做一步前提工作,那就是观察一个方格边长为2^n的时候的能最多分割的次数 t 为多少?
n = 0,t = 0
n = 1,t = 1
n = 2,t = 1 + 4
n = 3,t = 1 + 4 +4^2
……
n = m ,t = 4^0+4^1+……+4^(m-1)

t = 1*( 1 - 4^m ) / ( 1 - 4 )
我们得知到其实 一个方格的分割次数其实是 一个公比为4的等比数列求和后的结果。
这个结果我们可以大方地推广到 n,k的取值那里去。
首先知道
当n=31时,t=(1-4**31)/(1-4)=1537228672809129301
1537228672809129301
1000000000000000000=1e18
可以观察到,其实如果我们切割一个边长为2^(n-1)的方格为路,然后我们让正右下角的方格随便分割,都可以,
因为k<1e18,而当n>=32时,正右下角的方格可以分割为1537228672809129301次。
我们只要保留一条路,然后让k对我们路径无关的右下角的方格任意分割。
这就是我们第一次讨论,只要是根据输入的n,k的范围简单地筛选。
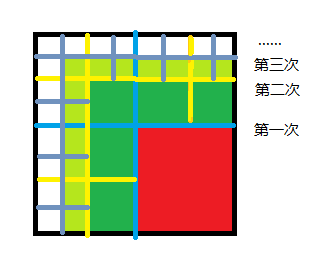
2、第二个讨论,其实我们知道只要我们保证围墙的方格的边长不变,我们其实可以随意,任意地操作。
不过我们分割是有顺序,顺序如下图(第一次,蓝色,第二次,黄色,第三次,蓝紫色)
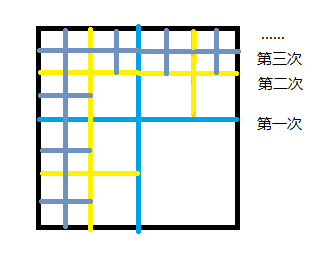
其实我们可以枚举一下,边长为:2^31~2^0,处理一下即可,我们其实知道,保证这条路,最少的切割次数,
就是如上图,输入边长为2^n,围墙的方格边长为2^m,最少切割次数为t
m=n , t=0
m=n-1, t=1
m=n-2, t=1+3
m=n-3, t=1+3+7
………………
其实我们可以发现,每一次增量是变化的,delta[ i ]= delta [ i-1 ] *2 +1
然后我们求一个前缀和即可,前缀和=保留围墙边长为2^m的最小切割次数。
有最少必定有最大(以下的算法其实是燕良兄提供的),
他说:最大,不就是,把这个总方格切割到最小,然后把围墙补回来就可以。
我们只要知道这个围墙是由多少个方格组成即可,因为,总方格切割到最小,我们是知道的。
因为前提工作那里就知道一个方格切割到最小 其实是: 公比为4的等比数列前n项之和。
那么现在问题是:我们怎么知道这个围墙的组成的方格数呢????
其实也是一个规律,而且这个规律和刚才的最少切割数的delta[ ] 数组是一样的。
就是delta [ i ] = delta [ i-1 ] * 2 + 1
贴上代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=50;
ll n,k;
ll A[N],B[N]; //其中A[],指的是最少切割次数,B[],指的是围墙的方格数
void init(){ //围墙边长为2^n,最少的切割次数A[n]
A[0]=0;
ll cur=0;
for(int i=1;i<31;i++){
cur=cur*2+1;
B[i-1]=cur;
A[i]=A[i-1]+cur;
}
}
ll sum(int x){ //等比数列求和_公比为4
ll ans=1;
for(int i=0;i<x;i++){
ans*=4;
}
ans=(ans-1)/3;
return ans;
}
int main()
{
int T;
init();
scanf("%d",&T);
while(T--){
scanf("%lld%lld",&n,&k);
if(n>31){
printf("YES %lld\n",n-1);
}else{
ll L,H,flag=0;
for(ll m=n;m>=0;m--){
L=A[n-m];
H=sum(n)-B[n-m]*sum(m);
//printf("(%lld %lld) %lld %lld \n",n,m,L,H);
if(L<=k&&k<=H){
printf("YES %lld\n",m);
flag=1;
break;
}
}
if(!flag){
printf("NO\n");
}
}
}
return 0;
}