Siamese Network

http://yann.lecun.com/exdb/publis/pdf/chopra-05.pdf

Learning a Similarity Metric Discriminatively, with Application to Face Verification

Abstract

我们提出一种方法来从数据中训练学习一个相似性的度量标准。这个方法可以被应用到识别或者验证任务中，并且在这些任务中训练时样本的类别数很大且未知，还有对于单一样本来说样本数很小。我们方法的思想就是去学习一个函数，这个函数可以将输入映射到一个目标空间里，使得目标空间里的L1范数可以近似等于输入空间中的“语义”距离。这个方法被我们应用到一个人脸验证任务中。学习过程是去最小化一个有区分性的损失函数，这个损失函数会驱使来自同一个人的人脸组合的相似度量小，使得来自不同人的人脸组合相似度量大。从输入到目标空间的映射是一个被设计来对几何空间扭曲鲁棒的卷积网络。我们在Purdue/AR 人脸数据集上进行测试。

1. Introduction

传统的分类方法是使用判别训练算法，如神经网络或者支撑向量机，这些方法都是需要提前已知所要区分的类别的。同时也需要对于所有的分类它们的样本数据都是可以得到的。还有就是，这些方法都内在地限定了总分类数相对是一个较小的数字（如100）。那么这些方法就不适用于样本分类数很大且每个分类样本数很小以及在训练时仅仅已知了部分分类的情况。这类应用就包括了人脸识别和人脸验证：类别数可能达到几百甚至几千，而且每一个分类只有很少的样本数。对于这类问题一个较为普遍的方法就是基于距离的方法，也就是计算被分类被验证的模式与存储原型之间的相似性度量。另一种普遍的方式就是在降维空间中使用非判别（生成）概率方法，也就是一个类的模型可以通过不使用别的类别的样本来训练得到。为了能够在这类应用中使用判别学习技术，我们必须设计一种方法能够从有的数据里提取出关于问题本身的信息，而且不需要关于类别的特定信息。
本篇提出的方法是从数据中学习一个相似度量。这个相似性度量在之后可以被用来对未知类的新样本（如训练中没见过的人的人脸）进行比较和匹配。我们提出一种新的判别训练算法来学习这个相似性度量。这种方法可以被应用到类别数大且所有类在训练时并不全部已知的分类问题中。
其主要想法是找到一个能够将输入映射到目标空间的函数，使得在目标空间中一个简单的距离（欧式距离）就能近似的表征输入空间的“语义”距离。更准确的说就是给一个被 $W$参数化的函数族 $G_W(X)$，我们要找到一个值使得参数 $W$能够让相似性度量 $E_W(X_1,X_2)=||G_W(X_1)-G_W(X_2)||$在 $X_1$和 $X_2$属于同一类时小，反之不同类就大。这个系统是由训练集的组合输入来训练的。通过训练后最小化的损失函数能够当 $X_1$和 $X_2$属于同一类时最小化 $E_W(X_1,X_2)$，当属于不同类时最大化 $E_W(X_1,X_2)$。对于 $G_W(X)$的本质我们不作假设除了对于参数 $W$要具有区分能力。因为带有相同参数 $W$的相同函数 $G_W(X)$要作用于两个输入，这个相似性度量是对称的。这被称作siamese结构。
为了使用这种方法搭建一个人脸验证系统，我们首先需要训练模型来生成输出向量，对于来自同一个人的图像组合的输出向量是紧挨的，对于来自不同人的图像组合的输出向量是相距较远的。这样的模型就能够用来作为在训练中没见过的新人物的人脸图像的一个相似性度量。
这个方法的很重要的一点就是在 $G_W(X)$的选取上完全自由。因此，我们使用被设计来提取出的特征具有对输入的几何扭曲鲁棒的结构模型，如卷积网络。那么得到的相似性度量对于组合图像中的姿态上小的不同会具有鲁棒性。
因为目标空间的维度低而且在该空间中的自然距离对于输入上的不相干扭曲是不变的，我们可以简单地从很小数量的样本来估计每个新类别的概率模型。

1.1. Previous Work

在比较之前就将人脸图像映射到低维目标空间的想法已经有很长的一段历史，这开始于基于PCA的特征脸方法，在这个方法里 $G(X)$是一个经过非判别训练的线性映射来最大化方差。基于LDA的Fisherface方法也是线性的，但是它是进行判别训练的来最大化类间和类内方差的比例的。非线性的基于Kernel-PCA和Kernel-LDA的延伸也被讨论过了。对于这些方法一个主要的缺点在于它们对于输入图像的几何变换（平移，缩放，旋转）和其他的一些变化（面部表情变化，是否佩戴眼镜，围巾）非常敏感。一些作者也提出过一些对于已知变换集合局部不变的相似性度量。一个例子是Tangent Distance方法。另一个例子是应用于人脸识别的弹性匹配。其他作者提倡采用基于扭曲的归一化算法来最大化地减少姿态引起的人脸面部的变化。所有这些方法的不变性都是事先人为设计的。而本文提出的方法，其不变性并不来自于关于任务的先验知识，而是模型自己从数据中学习来。当使用卷积网络作为映射函数时，我们设计的方法能够学习到呈现在数据中的大范围的不变性。
我们的方法在某种程度上和应用于签名验证的siamese结构有些相似。我们的方法和签名验证的方法相比最主要的不同在于通过训练过程最小化的损失函数的本质是不一样的。我们的损失函数来自于基于能量的模型的判别训练框架。
我们的方法和其他降维技术如多维缩放（Multi-Dimensional Scaling, MDS）和局部线性嵌入（Local Linear Embedding，LLE）是非常不同的。MDS是基于已知的两两不一致性从训练集中的每一个输入不构建映射来计算一个目标向量。相比之下，我们的方法生成一个非线性映射使得任意输入向量都可以被映射到相应的低维空间内。

2. The General Framework

概率模型是对被模型化的参数的每个可能的配置赋予一个归一化概率，而基于能量的模型（EBM）是给这些配置赋予一个非归一化的能量。这样的系统的预测是通过搜索使得能量最小的参数配置来完成的。EBMs被应用于不同配置的能量必须通过比较来进行决策（分类，验证等）的场景。一个可训练的相似性度量可以被视为联系能量 $E_W(X_1,X_2)$到一组输入上。在最简单的人脸验证场景下，我们简单的设定 $X_2$为已知身份的所有可得到的图像，然后将最小值 $E_W(X_1,X_2)$和预先设定的阈值进行比较。
EBMs相比于传统概率模型（尤其是生成模型）的优点在于我们不需要估计输入空间的归一化概率分布。没有了归一化，我们将不用再去计算可能无法解决的配分函数。同时这也给了我们更多模型选择的自由。
学习是通过在训练集上寻找能够最小化合理设计的损失函数的参数 $W$来进行的。第一印象，我们可能会认为简单地使用来自同一类别上输入组合来最小化 $E_W(X_1,X_2)$就足够了。但是这样一般会导致灾难性的崩溃：仅仅简单地通过将 $G_W(X_1)$置为常值函数就能将能量和损失函数变成0。因此我们的损失函数需要一个对比项来保证不仅来自同类的输入组的能量低，还要使来自不同类的输入组的能量大。如果使用恰当的归一化概率模型，这个问题就不会发生，因为让特定组别的概率高就会自动的使得其他组的概率低。

2.1. Face Verification with Learned Similarity Metrics

人脸验证任务就是接受或者拒绝图像中主体的声明身份。我们使用两种指标来判别模型的性能：一个是false accepts的比例和false rejects的比例。一个好的系统需要同时最小化这两个指标。
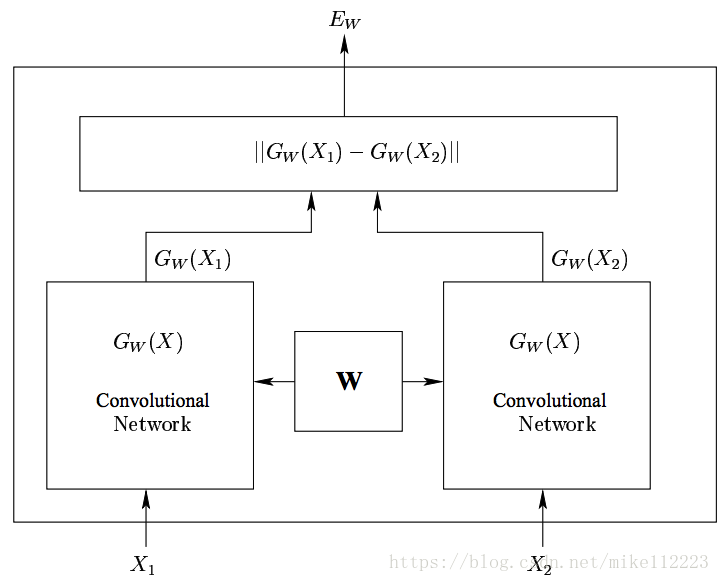
我们的方法是建立一个可训练的系统来将未经过处理的人脸图像映射到低维空间中的点上，来使得如果图像属于同一个人，那么这些点的距离就小，否则距离就大。学习这样一个相似性度量是通过训练一个卷积网络来实现的，这个卷积网络由两个相同的共享一套参数的卷积网络组成-Siamese Architecture（如图1）。

2.2. The energy function of the EBM

我们的学习系统的结构如图1。关于 $G_W(X)$结构的细节会在3.2节给出。

图1. Siamese Architecture

$X_1$和 $X_2$是系统的一组输入图像。 $Y$是输入组的一个0、1标签，如果 $X_1$和 $X_2$属于同一个人（是一组正对），那么 $Y=0$，否则 $Y=1$（是一组负对）。 $W$是学习的共享参数向量， $G_W(X_1)$和 $G_W(X_2)$是通过映射 $X_1$和 $X_2$生成的低维空间中的两个点。我们的系统可以被视为是一个标量“能量方程” $E_W(X_1,X_2)$，它可以用来表征 $X_1$和 $X_2$的匹配程度。定义如下：
$E_W(X_1,X_2)=||G_W(X_1)-G_W(X_2)|| \tag 1$
从训练集中随意找出一组正对 $(X_1,X_2)$和一组负对 $(X_1,X'_2)$，如果满足下面条件，那么系统就表现的很理想：
$\mathbf {condition 1:} \exists m>0, \text {such that } E_W(X_1,X_2)+m<E_W(X_1,X_2')$
正数 $m$被视为margin。
为了简化注释，在论文之后的部分 $E_W(X_1,X_2)$被写作 $E_W^G$， $E_W(X_1,X_2')$则被表示为 $E_W^I$。

2.3. Contrastive Loss Function used for Training

我们假设损失函数只是间接地通过能量依赖于输入和参数。我们的损失函数的形式是：

$\mathcal L(W) = \sum^P_{i=1}L(W,(Y,X_1,X_2)i) \\ L(W,(Y,X_1,X_2)^i) = (1-Y)L_G(E_W(X_1,X_2)^i) +YL_I(E_W(X_1,X_2)^i)$

$(Y,X_1,X_2)^i$表示第i个样本，是由一组输入图像和一个标签（1或0）组成， $L_G$是正对部分的损失函数， $L_I$是负对部分的损失函数， $P$代表训练样本的数目。 $L_G$和 $L_I$需要被设计来使得最小化 $L$能够减少正对的能量，并同时增加负对的能量。一种简单的方式来实现就是让 $L_G$是单调增的， $L_I$是单调减的。然而，这儿存在一个更加普遍的条件集合，使得在该条件集合下，最小化 $L$能够让系统接近条件1。我们提出的方法和LeCun提出的相似，我们考虑一个由带有能量 $E_W^G$的正对 $(X_1,X_2)$和带有能量 $E_W^I$的负对 $(X_1,X_2')$组成的一个训练集。我们定义：
$H(E_W^G,E_W^I)=L_G(E_W^G)+L_I(E_W^I) \tag 2$
作为这两对的总损失函数。我们假设 $H$对于两个能量来说是具有凸性的（注意：我们并不假设 $H$对于 $W$具有凸性）。我们还假设存在一个 $W$对于单一训练样本来说条件1是满足的。那么对于所有的 $E_W^G$和 $E_W^I$，损失函数 $H$一定满足下列条件：
$\mathbf {Condition2}: \text{$H(E_W^G,E_W^I)$的最小值应当位于这个$E_W^G+m<E_W^I$的半平面内。}$
这个条件明确地保证了当根据 $W$来最小化 $H$时，系统会被驱使到满足条件1的区域里去。
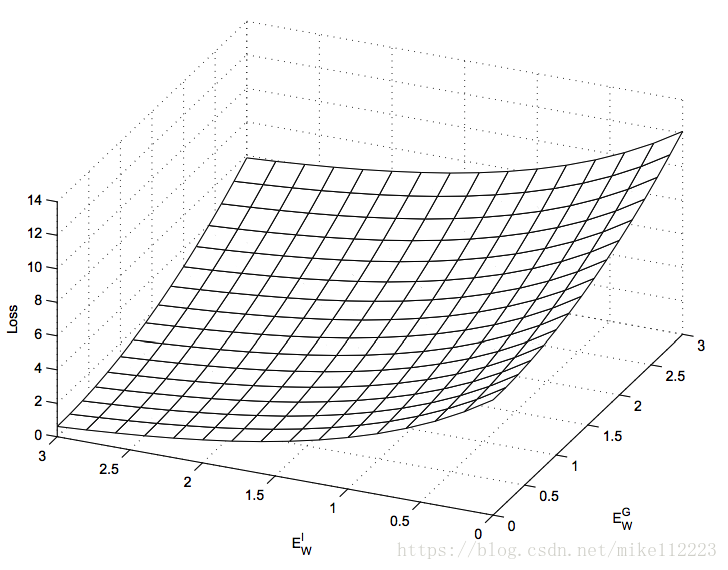
如图2，对于 $H$的最小值位于无穷的情况，下列条件是充分的：
$\mathbf {Condition3}: \text{位于margin line $E_W^G+m=E_W^I$ 上的$H(E_W^G,E_W^I)$的负梯度和[-1,1]方向拥有正的点乘积}。$

图2. 三维坐标下，损失函数 $H$相对于 $E_W^G$和 $E_W^I$的图像。

为了证明这个，我们需要陈述和证明下列理论。
$\mathbf {Theorem 1:} \text{让$H(E_W^G,E_W^I)$在$E_W^G$和$E_W^I$上具有凸性并且在无穷处具有最小值。假设存在一个$W$使得一个样本点满足条件1。如果条件三满足，那么根据$W$最小化$H$将驱使找到一个满足条件1的$W$}$

图3. 展示了两个半平面 $HP_1$和 $HP_2$以及可行域 $R$。

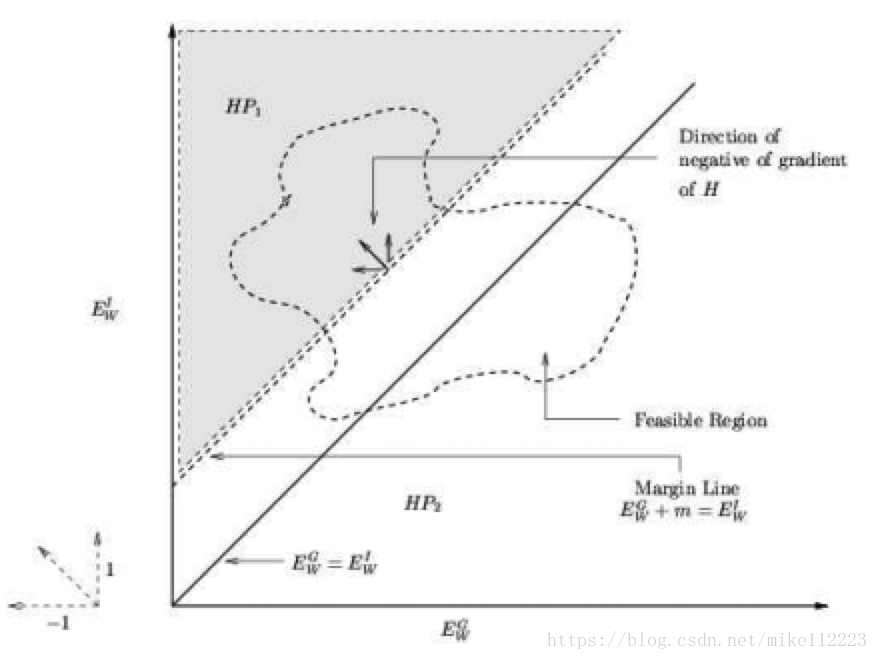
Proof. 考虑由 $E^G_W$和 $E^I_W$构成的正四分之一平面（也就是坐标系的第一象限，如图3）。使用 $HP_1$和 $HP_2$来分别表征 $E^G_W+m<E^I_W$和 $E^G_W+m\ge E^I_W$这两个半平面。我们要在（ $W$的领域里的所有值所构成的） $E^G_W$和 $E^I_W$上来最小化 $H$函数。我们定义位于这四分之一平面内的区域 $R$是由 $W$的领域里的所有值所构成的 $E^G_W$和 $E^I_W$所组成的。最一般的对于 $R$的设定就是 $R$是非凸的，而且可以位于这个平面内的任意位置。然而由于我们提前进行了假设，也就是至少存在一个 $W$使得满足条件1，通过这个前提，我们可以有 $R$必和半平面 $HP_1$有交集。为了在条件3的情况下证明理论1，我们需要证明至少存在一个位于 $R$和 $HP_1$交集里的点，满足它的损失函数 $H$值是小于 $R$和 $HP_2$交集里的所有点的。
定义 $E^*_G$为margin line $E^G_W+m=E^I_W$上的点并且是这条线上所有点里 $H$最小的，也就是
$E^*_G=\text{argmin}\{ H(E^G_W,E^G_W+m)\} \tag 3$
因为在margin line上的所有点关于 $H$的负梯度的方向都是位于 $HP_1$这个半平面内的（条件三），通过 $H$的凸性，我们有
$H(E^*_G,E^*_G+m) \le H(E^G_W,E^I_W) \tag 4$
当 $E^G_W+m > E^I_W$.
现在考虑一个离 $(E^*_G,E^*_G+m)$距离 $\epsilon$的点，并且位于 $HP_1$半平面内，也就是
$H(E^*_G-\epsilon,E^*_G+m+\epsilon) \tag 5$
使用一阶泰勒展开，我们可将上式写成:
$H(E^*_G-\epsilon,E^*_G+m+\epsilon) \\ = H(E^*_G,E^*_G+m) - \epsilon \frac{\partial H}{\partial E^G_W} + \epsilon \frac{\partial H}{\partial E^I_W} + O(\epsilon^2) \\ = H(E^*_G,E^*_G+m)+\epsilon \left[ \frac{\partial H}{\partial E^G_W} \frac{\partial H}{\partial E^I_W} \right] \left[ \begin{array}{} -1\\ 1 \end{array} \right]+O(\epsilon^2) \tag 6$
通过条件3，方程6右边第二项就为负，因此对于足够小的 $\epsilon$,
$H(E^*_G-\epsilon,E^*_G+m+\epsilon) \le H(E^*_G,E^*_G+m)$
因此存在一个点位于区域 $R$和半平面 $HP_1$的相交区域内，并且损失函数值是小于区域 $R$和半平面 $HP_2$的相交区域内任意一点的。因此得证。

需要注意的是，我们是要在条件三下来证明理论一的。而只要对于 $H$任何时候 $L_0$都是单调增函数，并且 $L_1$都是单调增函数，那么条件三就成立。
对于单一样本，我们所使用的准确的损失函数是
$L(W,Y,X_1,X_2)=(1-Y)L_G(E_W)+YL_I(E_W) \tag 8$ $=(1-Y) \frac{2}{Q}(E_W)^2+(Y)2Qe^{-\frac{2.77}{Q}E_W} \tag 9$
$E_W=||G_W(X_1)-G_W(X_2)||$。在我们的结构中， $G_W$是有界的，因此 $E_W$也是有界的。常数 $Q$就被设定为 $E_W$的上边界。
可以很明显的看出来上述损失函数对于 $E_W^G$是单调增，对于 $E_W^I$是单调减，对于 $E_W^G$和 $E_W^I$上都具有凸性。因此通过之前的论述，我们可以得出这个损失函数会驱使 $W$到一个理想的值，使得模型表现理想。
此外，对于我们的损失函数再做两点更深入的讨论。第一，损失函数的常量已经解释过了。我们最小化损失函数的优化算法是基于梯度的。那么这些常量的选择能够保证在margin线上，损失函数的负梯度总是指向区域 $R$里的，这一点就避免了我们的算法会在停滞在一些点上，这些点是位于 $R$边界且梯度指向 $R$之外的点。在这样的情况下，基于梯度的优化算法就能确保到达损失函数的局部最优点并且终止。
第二，我们必须强调对于能量来说使用平方范数相比于 $L_1$范数来说不是很合适。确实，如果能量是两个输出向量的差的平方范数的话，那么能量的对于参数的梯度会在能量趋近于0的时候消失。这会在损失函数上创造初一片很危险的平缓区域。这会使得模型在学习一些样本的时候失败，如两个彼此为负样本的图像对应的能量趋近于0.

2.4. Convolutional Networks

为了将原始图像映射到低维空间中并且生成一个经过学习的相似性度量指标，我们使用两个共享参数的卷积网络（见图1）。卷积神经网络是可以训练的，多层的，非线性系统，它可以端对端的通过像素级的操作来完成底层特征到高层语义特征的学习。它最主要的优势在于能够学习一个最优的具有局部特征平移不变性的检测器，而且学习出来的特征对于输入图像的几何扭曲具有一定的鲁棒性。

3. Experiments

第一个实验用到的数据集，AT&T Database of Faces，是一个相对小的数据集，一共400张图，40个对象，每个对象10张图，这10张图会在亮度，人脸表情，配饰，头部位置上有变化。每张图112x92像素，灰度图，且会crop到只包括脸。
第二个实验用到的数据集，AR Database of Faces和Feret Database的一个子集。训练集来自这两个数据集，测试集只来自AR。
AR包含3526张图，136个对象，每个对象26张图，这26张图分为2组13张，间隔14天拍摄，13张里4张表情变换，3张亮度变换，3张戴深色墨镜和亮度变换，3张围巾把脸部分挡住和亮度变换。由于该数据集中，脸并没有位于图像中央，所以需要做一个简单的置中算法。
Feret Database，14051张图来自1209个对象，我们使用子集用于训练，子集包含1122张图，187个对象，每个6张图。
所有的图像初始化只有裁剪和降采样到56x46。
Partitioning 首先训练集和测试集需要分开，然后各自在各自的数据集中生成正负样本对。
对于AT&T，前350张图，35个对象为训练集，后50张图，5个对象为测试集，那么训练集就有3500（351010）对正样本，119000对负样本。

对于训练来说，我们保证正负样本数量相同，也就是一半正样本，一半负样本。