【组合计数】【莫队】博弈论与概率统计CodePlus2018三月赛D题

分析：

种种神奇的原因（TYP对TLY无脑崇拜，TLY证了一个结论，TYP就说TLY把这题秒了），导致我以为是结论题，猜了半天。。。F***

其实是一道有点坑的组合计数。

首先，要明确题意：这题问的是在已确定输赢次数条件下概率，换句话说，每种局面发生的概率相同，且和为1。题目中给出的p是没用的。

要输出一个分数，分母很好求，就是一个组合数 $C(n+m,n)$

分子如果O(N)也很好算：

枚举最终得分k，可以算出答案为k的方案数：
K确定后，就能知道0分状态下输掉的次数。受到NOI2018D1T2冒泡排序的启发，我们可以用一条在网格上的路径来表示一种局面。

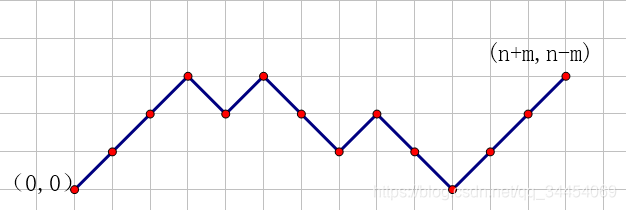
在这里插入图片描述
（上图是k=n-m时的某种方案，此时不存在0分时失败的情况）
每往上走一步，就代表胜利一次，往下走一步就代表失败一次。
为了保证合法性，不能碰到y=-1这条线。而碰到这条线的方案数为C(n+m,n+1)（可以将第一次与x轴接触的地方，将前半部分上下翻转，起点就一定会变为点(0,-1)，相当于从(0,-1)到达(n+m,n-m)的路径数）
此时的方案数为碰到y=0的方案数-碰到y=-1的方案数=C(n+m,n)-C(n+m,n+1)

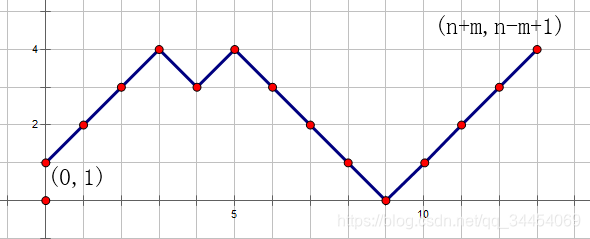
在这里插入图片描述
这是k=n-m+1时的某种方案，此时有且仅有一次在0分时失败的情况，此时分数不降，方便起见，我们可以先把这一分先加上，使得图像保持只向上/向下。

这时，为了保证方案的合法性（即存在“0分时失败”的情况），我们要求其必然至少一次碰到y=0这条线，那么此时的方案数应该为：碰到y=0的方案数-碰到y=-1的方案数=C(n+m,n+1)-C(n+m,n+2)

……

所以，就可以得到最终的答案：
$\sum_{k=n-m}^{k\leq n}k*(C(n+m,k+m)-C(n+m,k+m+1))$

这是对于 $n\geq m$ 的情况，而对于 $n<m$ 的情况，则并没有太大区别（其实是完全一样的，只不过还要限制最终得分非负）

这就是 $O(NT)$ 算法了。（为什么这就值30分？？？）

最后就比较套路了：
这个式子可以通过拆开括号：
$(n-m)C(n+m,n)-(n-m)C(n+m,n+1)$
$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +(n-m+1)C(n+m,n+1)-(n-m+1)C(n+m,n+2)$
$+……$
领位相减： $(n-m)C(n+m,n)+C(n+m,n+1)+C(n+m,n+2)……$
最终得到： $(n-m)C(n+m,n)+\sum_{i=0}^{i<m}C(n+m,i)$
对于 $n\geq m$ 的情况，答案为： $(\sum_{i=0}^{i<m} C(n+m,i))+(n-m)C(n+m,n)$
对于 $n<m$ 的情况，答案为： $\sum_{i=0}^{i<n} C(n+m,i)$

变成组合数前缀和的形式之后，设答案 $f(i,j)=\sum_{k=0}^{k\leq j}C(i,k)$
然后就可以O(1)转移到相邻位置：
$f(i+1,j)=f(i,j)*2-C(i,j)$
$f(i,j+1)=f(i,j)+C(i,j+1)$

然后就可以用莫队算法， $O(N\sqrt N)$ 算答案了。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
#define SF scanf
#define PF printf
#define MAXN 250010
#define MOD 1000000007
using namespace std;
typedef long long ll;
ll fac[MAXN],inv[MAXN],blo[MAXN];
int n,m,t;
ll ans[MAXN],ans2[MAXN];
struct node{
	int x,y;
	int	id;
	bool operator <(const node &a) const {
		if(blo[x]!=blo[a.x])
			return blo[x]<blo[a.x];
		return y<a.y;
	}
}que[MAXN];
ll ans1;
ll C(int x,int y){
	return fac[x]*inv[y]%MOD*inv[x-y]%MOD;
}
const ll inv2=(MOD+1ll)>>1ll;
void change(int &x,int &y,int adx,int ady){
	if(adx==1){
		ans1=(ans1+C(y,x+1))%MOD;
		x++;
	}
	if(ady==1){
		ans1=((ans1*2ll-C(y,x))%MOD+MOD)%MOD;	
		y++;
	}
	if(adx==-1){
		ans1=(ans1-C(y,x)+MOD)%MOD;
		x--;
	}
	if(ady==-1){
		ans1=(ans1+C(y-1,x))%MOD*inv2%MOD;
		y--;
	}
}
void prepare(){
	fac[0]=1;
	for(int i=1;i<=250000;i++) fac[i]=fac[i-1]*i%MOD;	
	inv[0]=inv[1]=1;
	for(int i=2;i<=250000;i++) inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;
	for(int i=1;i<=250000;i++) inv[i]=inv[i-1]*inv[i]%MOD;
	
	int siz=700;
	for(int i=1;i<=250000;i++)
		blo[i]=i/siz+1;
}
ll fsp(ll x,int y){
	ll res=1;
	while(y){
		if(y&1)
			res=res*x%MOD;
		x=x*x%MOD;
		y>>=1;
	}
	return res;
}
int main(){
	prepare();
	int p;
	SF("%d%d",&t,&p);
	for(int i=1;i<=t;i++){
		SF("%d%d",&n,&m);
		que[i].x=min(n-1,m-1);
		ans2[i]=fsp(C(n+m,n),MOD-2);
		que[i].y=n+m;
		if(n>m)
			ans[i]+=(n-m)*C(n+m,n)%MOD;
		que[i].id=i;
	}
	sort(que+1,que+1+t);
	int l=0,r=0,now=0;
	ans1=1;
	while(++now<=t){
		while(r<que[now].y)
			change(l,r,0,1);
		while(l<que[now].x)
			change(l,r,1,0);
		while(l>que[now].x)
			change(l,r,-1,0);
		while(r>que[now].y)
			change(l,r,0,-1);
		(ans[que[now].id]+=ans1)%=MOD;
	}
	for(int i=1;i<=t;i++)
		PF("%lld\n",ans[i]*ans2[i]%MOD);
}

【组合计数】【莫队】博弈论与概率统计CodePlus2018三月赛D题

分析：

猜你喜欢