朴素贝叶斯（naïve Bayes） 法是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集， 首先基于特征条件独立假设学习输入/输出的联合概率分布； 然后基于此模型， 对给定的输入x， 利用贝叶斯定理求出后验概率最大的输出y。 朴素贝叶斯法实现简单， 学习与预测的效率都很高， 是一种常用的方法。
1. 朴素贝叶斯法的学习与分类
基本方法
训练数据集：
由X和Y的联合概率分布P(X,Y)独立同分布产生
朴素贝叶斯通过训练数据集学习联合概率分布P(X,Y) ，
即先验概率分布：
及条件概率分布：
注意： 条件概率为指数级别的参数：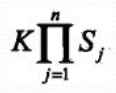
条件独立性假设：
“朴素” 贝叶斯名字由来， 牺牲分类准确性。
贝叶斯定理：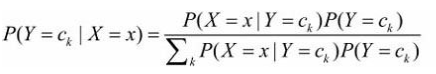
代入上式：
这是朴素贝叶斯法分类的基本公式。 于是， 朴素贝叶斯分类器可表示为
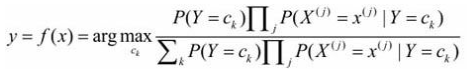分母对所有ck都相同：
后验概率最大化的含义
朴素贝叶斯法将实例分到后验概率最大的类中， 等价于期望风险最小化，
假设选择0-1损失函数： f(X)为决策函数
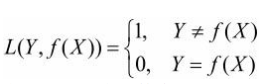
期望风险函数：
取条件期望：
只需对X=x逐个极小化， 得：
推导出后验概率最大化准则：
2. 朴素贝叶斯法的参数估计
应用极大似然估计法估计相应的概率，先验概率P(Y=ck)的极大似然估计是：
设第j个特征x(j)可能取值的集合为：
条件概率的极大似然估计：
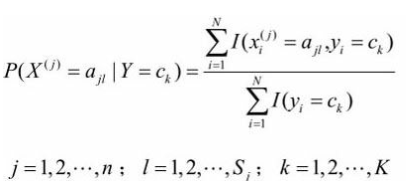
学习与分类算法Naïve Bayes Algorithm：
输入：
训练数据集：
，其中
第i个样本的第j个特征，
，
是第j个特征可能取的第l个值，j＝1,2,…,n， l＝1,2,…,Sj， yi∊{c1， c2,…,cK}。
输出：
x的分类
步骤：
（1） 计算先验概率及条件概率
（2） 对于给定的实例x＝(x(1),x(2),…,x(n))T， 计算
（3） 确定实例x的类
3、简单实现的代码
以下是天气的打球的14条信息：
有4个属性会决定play，每个属性又有若干个特征，预测sunny,cool,high,TRUE是否会play.
结合上面的知识，本例子大概步骤如下：
（1）计算先验概率(yes和no)
（2）计算每个属性的特征集合对应yes和no概率
（3）计算预测概率
下面是我写的代码，没有用第三方包写的：
data_list = [
['sunny', 'hot', 'high', 'FALSE', 'no'],
['sunny', 'hot', 'high', 'TRUE', 'no'],
['overcast', 'hot', 'high', 'FALSE', 'yes'],
['rainy', 'mild', 'high', 'FALSE', 'yes'],
['rainy', 'cool', 'normal', 'FALSE', 'yes'],
['rainy', 'cool', 'normal', 'TRUE', 'no'],
['overcast', 'cool', 'normal', 'TRUE', 'yes'],
['sunny', 'mild', 'high', 'FALSE', 'no'],
['sunny', 'cool', 'normal', 'FALSE', 'yes'],
['rainy', 'mild', 'normal', 'FALSE', 'yes'],
['sunny', 'mild', 'normal', 'TRUE', 'yes'],
['overcast', 'mild', 'high', 'TRUE', 'yes'],
['overcast', 'hot', 'normal', 'FALSE', 'yes'],
['rainy', 'mild', 'high', 'TRUE', 'no']
]
# 计算出现次数
def get_count(indexs,attrs):
'''
indexs:待比较的索引列表
attrs:待比较的属性列表
'''
count = 0
for i in data_list:
if len(indexs) == 1 and i[indexs[0]] == attrs[0]:
count += 1
else:
flag = True
for j in range(len(indexs)):
if i[indexs[j]] != attrs[j]:
flag = False
if flag:
count += 1
return count
# 计算先验概率
yes_count = get_count([4],['yes'])
P_yes,P_no = yes_count/len(data_list),(len(data_list) - yes_count)/len(data_list)
print('先验概率yes:%f,no:%f' %(P_yes,P_no))
# 计算每个属性的特征集合
attr_set_list = []
for i in range(4):
attr_set = []
for j in data_list:
attr_set.append(j[i])
attr_set_list.append(list(set(attr_set)))
print(attr_set_list)
# 计算每个属性的特征集合对应yes和no概率
predict_dict = {}
for i in range(len(attr_set_list)):
for j in attr_set_list[i]:
predict_dict[j] = [get_count([i,4],[j,'yes'])/yes_count,get_count([i,4],[j,'no'])/(len(data_list) - yes_count)]
print(predict_dict)
# 计算预测概率
def get_predict_p(predict_features):
p_yes,p_no = P_yes,P_no
for i in predict_features:
p_yes *= predict_dict[i][0]
p_no *= predict_dict[i][1]
return p_yes,p_no
predict_features = ['sunny','cool','high','TRUE']
print(get_predict_p(predict_features))运行结果：
可以看到预测时yes的概率约为0.0053，no的概率约为0.0206。还原手算：
p_yes = 2/9×3/9×3/9×3/9×9/14=0.0053, p_no = 3/5×1/5×4/5×3/5×5/14=0.0206。验证了上面的程序。
但是，问题并没有解决，看上面的overcast，no的概率为0，即只要特征有overcast就一定打球，这违背了朴素贝叶斯的基本假设：输出依赖于所有的属性。解决0概率的问题主要有平滑算法，数据平滑的方法很多，最简单的是拉普拉斯估计（Laplace estimator）--即在算每个feature的yes和no的概率时为每个特征的计数都加1，每个特征的计数加1时对应的yes和no也都加1，这是累加的，也就是说，每个属性有多少个特征，对应yes和no在计算时就加多少个。
其实要改动的代码不多，主要是在计算先验概率和计算每个属性的特征集合对应yes和no概率时做处理，直接上代码：
data_list = [
['sunny', 'hot', 'high', 'FALSE', 'no'],
['sunny', 'hot', 'high', 'TRUE', 'no'],
['overcast', 'hot', 'high', 'FALSE', 'yes'],
['rainy', 'mild', 'high', 'FALSE', 'yes'],
['rainy', 'cool', 'normal', 'FALSE', 'yes'],
['rainy', 'cool', 'normal', 'TRUE', 'no'],
['overcast', 'cool', 'normal', 'TRUE', 'yes'],
['sunny', 'mild', 'high', 'FALSE', 'no'],
['sunny', 'cool', 'normal', 'FALSE', 'yes'],
['rainy', 'mild', 'normal', 'FALSE', 'yes'],
['sunny', 'mild', 'normal', 'TRUE', 'yes'],
['overcast', 'mild', 'high', 'TRUE', 'yes'],
['overcast', 'hot', 'normal', 'FALSE', 'yes'],
['rainy', 'mild', 'high', 'TRUE', 'no']
]
# 计算出现次数
def get_count(indexs,attrs):
'''
indexs:待比较的索引列表
attrs:待比较的属性列表
'''
count = 0
for i in data_list:
if len(indexs) == 1 and i[indexs[0]] == attrs[0]:
count += 1
else:
flag = True
for j in range(len(indexs)):
if i[indexs[j]] != attrs[j]:
flag = False
if flag:
count += 1
return count
# 计算先验概率
yes_count = get_count([4],['yes']) + 1
P_yes,P_no = yes_count/(len(data_list)+2),(len(data_list) + 2 - yes_count)/(len(data_list)+ 2)
print('先验概率yes:%f,no:%f' %(P_yes,P_no))
# 计算每个属性的特征集合
attr_set_list = []
for i in range(4):
attr_set = []
for j in data_list:
attr_set.append(j[i])
attr_set_list.append(list(set(attr_set)))
print(attr_set_list)
# 计算每个属性的特征集合对应yes和no概率
predict_dict = {}
for i in range(len(attr_set_list)):
for j in attr_set_list[i]:
predict_dict[j] = [(get_count([i,4],[j,'yes'])+1)/(yes_count+len(attr_set_list[i]) - 1),(get_count([i,4],[j,'no'])+1)/(len(data_list) - yes_count + 1 +len(attr_set_list[i]))]
print(predict_dict)
# 计算预测概率
def get_predict_p(predict_features):
p_yes,p_no = P_yes,P_no
for i in predict_features:
p_yes *= predict_dict[i][0]
p_no *= predict_dict[i][1]
return p_yes,p_no
predict_features = ['sunny','cool','high','TRUE']
print(get_predict_p(predict_features))
为了方便，我在计算先验概率直接手动给yes_count加了1,所以后面在计算每个属性的特征集合对应yes和no概率时要减去1。
结果：
此时就没有了0概率，让我们也手动验证一下：
此处strong就是TRUE，可见程序结果是正确的。
以上内容均出自李航老师的《统计学习方法》。