前言

朋友，你通过各种不同的途经初次接触支持向量机（SVM）的时候，是不是会觉得这个东西耳熟能详，感觉大家都会，却唯独自己很难理解？
每一次你的老板或者同仁让你讲解SVM的时候，你觉得你看过这么多资料，使用过这么多次，讲解应该没有问题，但偏偏在分享的时候结结巴巴，漏洞百出？
每一次机器学习相关的面试在问到支持向量机（SVM）的时候，尽管你觉得你都准备好了，可是一次又一次败下阵来，以至于觉得问那些问题的人（是不是脑子有…）是那么的厉害，每一次都能精准发觉到你的不足和漏洞，让你怀疑你掌握的是假的SVM，然后让你怀疑人生？
那还等什么，快来看看这篇文章吧，原价998，现在只要。。。（不好意思，扯偏了。）

以上可能真的只是我的个人经历（在这里，学渣给各位大佬鞠躬了！），但不管怎么样，我还是要自己写一篇从头到尾的SVM的理解，然后呈现给各位大佬审阅，欢迎您批评指正！

按照以下问题成文：

由线性分类任务开始
为何需要最大化间隔
怎么解决凸二次规划问题
对偶问题的求解
SMO算法
核函数的由来和使用

SVM由线性分类开始

在这之前，假设读者们对线性分类模型和向量矩阵求导有大概的了解。

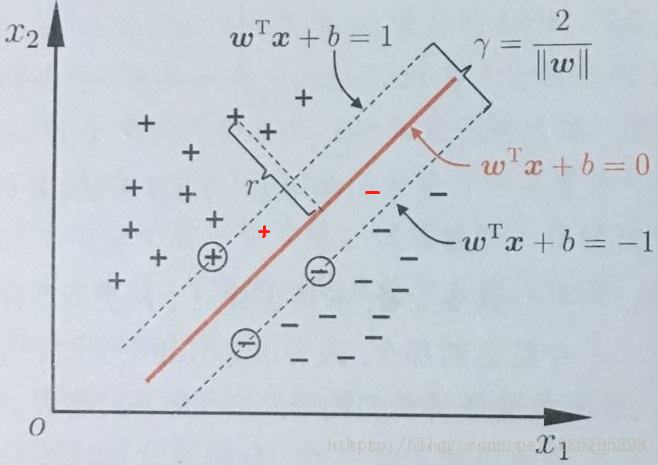
给定训练样本集 $D={(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{m},y_{m})))}, y_{i}\in \left \{ -1, 1\right \}$ , 线性分类器基于训练样本D 在二维空间中找到一个超平面来分开二类样本。当然，这样的超平面有很多。

这里写图片描述

但我们可以直观感受到，这根红色线代表的超平面抗“扰动”性最好。这个超平面离直线两边的数据的间隔最大，对训练集的数据的局限性或噪声有最大的“容忍”能力。

在这里，这个超平面可以用函数 $f(x) = w^{T}x+b$ 表示。当 $f(x)$ 等于0的时候，x便是位于超平面
上的点，而 $f(x)$ 大于0的点对应 y=1 的数据点， $f(x)$ 小于0的点对应y=-1的点。

为什么是 $y_{i}\in \left \{ -1, 1\right \}$ ,换句话说， $y$ 只能是-1，和1吗？不能是 $y$ =-100 表示反例， $y$ =2000表示正例，或 $y$ =0表示反例， $y$ =300表示正例，或 $y$ =5表示反例 $y$ =-7 表示正例吗？当然可以。y 只是一个label ，标注为{-1，+1}不过为了描述方便。

若 $y$ =0表示反例， $y$ =300表示正例，只不过分正类的标准变为 $（y-150）*f（x)>0$

不妨令：

$\left\{\begin{matrix}w^{T}x_{i}+b \geqslant +1, y_{i} = +1 ;& \\ w^{T}x_{i}+b \leq -1, y_{i} = -1 & \end{matrix}\right.$

为什么可以这么令呢？我们知道，所谓的支持向量，就是使得上式等号成立，即最靠近两条虚边界线的向量。那么，不难理解当 $w^{T}x+b$ 的值大于+1，或小于-1的时候，就更加支持“样本的分类”了。为什么要这么令呢？还是为了计算方便。接着往下看，你一定能悟到这么令的原因。

我们可以计算得到空间中任意样本点 $x$ 到超平面的距离为： $r = \frac{|w^{T}x+b|}{\left \| w \right \|}$ 。为什么呢？
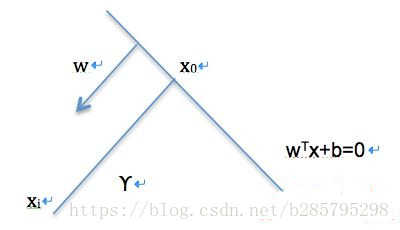
这里写图片描述
如图所示，有： $x = x_{0}+r\frac{w}{\left \| w \right \|}$ (简单平面几何)
又有： $w^{T}x_{0}+b = 0$ ，代入上式，求得： $r = \frac{|w^{T}x+b|}{\left \| w \right \|}$ 。

因为 $y_{i}\in \left \{ -1, 1\right \}$ ,，两个异类支持向量到超平面的距离之和（也称为“间隔”）可表示为： $r = \frac{2}{\left \| w \right \|}$ 。

很显然，我们要找到符合这样一个条件的超平面来分开两类数据：
这个超平面离两类样本都足够远，也就是使得“间隔”最大。即最终确定的参数 $w 和 b$ ,使得 $r$ 最大。即要：

$_{w,b}^\textrm{max}\frac{2}{\left \| w \right \|}$
$s.t. y_{i}( w^{T}x_{i}+b)\geq 1，i=1,2,...,m$

这等价于

$_{w,b}^\textrm{min}\frac{1}{2}{\left \| w \right \|}^{2}$
$s.t. y_{i}( w^{T}x_{i}+b)\geq 1，i=1,2,...,m$

由此我们得到了SVM的基本型。

凸优化

我们可以看到，上面的基本型目标函数是二次的，约束条件是线性的，这是一个凸二次规划问题。可以直接用现成的优化计算包求解。但若利用“对偶问题”来求解，会更高效。

啥是凸？什么是凸优化？

凸优化说的是这么一回事情，
$X\subset R^{n}$ 为一凸集， $f:X\rightarrow R$ 为一凸函数，凸优化就是要找出一点 $x^{*} \in X,$ 使得任意 $x \in X,$ 都满足 $f(x^{*})\leq f(x)$ .
可以想象成给我一个凸函数，我要去找到最低点。当然凸优化是一个很大很厉害的领域，在这里，我们只需要知晓这个问题是这么一回事。然后，这回事要怎么样求解，就好，有兴趣的朋友可以参考凸优化的概念或者Stephen Boyd & Lieven Vandenberghe 的《Convex Optimization》。
为啥叫二次规划问题呢？

据了解（其实就是知道），目标函数和约束条件都为变量的线性函数，叫做—–线性规划问题。
目标函数为变量的二次函数和约束条件为变量的线性函数，叫做—–二次规划问题。
目标函数和约束条件都为非线性函数，叫做—–非线性规划问题。

对偶问题

对于
$_{w,b}^\textrm{min}\frac{1}{2}{\left \| w \right \|}^{2}$
$s.t. y_{i}( w^{T}x_{i}+b)\geq 1，i=1,2,...,m$
为了后面的描述方便，记这个式子为（1）式。

使用**拉格朗日乘子法**可以得到其“对偶问题”。
这是拉格朗日对偶性，即，通过给每一个约束条件加上一个拉格朗日乘子。然后定义出拉格朗日函数，通过拉格朗日函数将约束条件融合进目标函数中。目的是，只需要通过一个目标函数包含约束条件，便可以清楚解释问题。

比如对（1）式每一个约束（共有m个约束， $y_{i}( w^{T}x_{i}+b)\geq 1$ ），添加拉格朗日乘子 $\alpha _{i} \geq 0$ ,则整个问题的拉格朗日函数可写为：

$L(w,b,\alpha )= \frac{1}{2}\left \|w\right \| ^{2} +\sum _{i=1}^{m}\alpha ^{i}(1- y_{i}( w^{T}x_{i}+b))$

为什么使用这样的拉格朗日乘子，又为何这样构建？这实际上是因为我们的目标函数是不等式约束，解这样的二次规划问题，我们选择用KKT条件，而KKT条件需要这样的一个约束 $\alpha _{i} \geq 0$ 。最终我们便通过KKT条件来产生原问题的对偶问题。
同样的，将上面这个式子记为（2）式。

可以看到，由于 $\alpha _{i} \geq 0$ , 这样，但凡有约束条件之一不满足，如 $y_{k}( w^{T}x_{k}+b)< 1$ ），

$L(w,b,\alpha )= \infty$ 。只有约束条件均满足的时候，

$L(w,b,\alpha )$ 有最优值，为 $L(w,b,\alpha )= \frac{1}{2}\left \|w\right \| ^{2}$

所以优化 $\frac{1}{2}\left \|w\right \| ^{2}$ 等价于优化 $L(w,b,\alpha )$ 当然，要满足约束条件 $\alpha _{i} \geq 0$ 。

于是，我们的目标函数可以表示为：

$_{w,b}^{min}$ $_{_{\alpha\geq 0}}^{max}$ $L(w,b,\alpha )$

满足一定条件下，等价于（注意，这个满足一定条件，是指满足KKT条件）

$_{_{\alpha\geq 0}}^{max}$ $_{w,b}^{min}$ $L(w,b,\alpha )$

后者把最小和最大的位置交换，这样使得运算方便起来。

KKT条件

什么是KKT条件？其实在这之前，本文有稍微有提到过。在这里正式介绍一下。

KKT条件是一个线性规划问题能有最优解的充分和必要条件。

一般地，一个最优化数学模型可以表示成如下形式：

$minf(x)$
$s.t. h_{i}(x) = 0 , i = 1,2,...,p$
$g_{j}(x) \leq 0 , j = 1,2,...,q$
$x\in X \in R^{n}$ $

$h(x)$ 是等式约束。
$g(x)$ 是不等式约束。
$p,q$ 表示约束的数量。

而这个最优化数学模型的最优解 $x^{*}$ 须满足的条件，即KKT条件为：

$h_{i}(x^{*}) = 0 , i = 1,2,...,p 和$ $g_{j}(x^{*}) = 0 , j = 1,2,...,q$
$\bigtriangledown f(x^{*}) + \sum_{i=1}^{p}\lambda _{i}\bigtriangledown h_{i}(x^{*}) + \sum_{j=1}^{q} \mu _{k}\bigtriangledown g_{k}(x^{*}) = 0$
$\lambda _{i}\neq 0, \mu _{k}\geq 0, \mu _{k}g_{k}(x^{*}) = 0$

于是我们的整个问题转化为

$L(w,b,\alpha )$ 对 $w,b$ 求最小
再对 $\alpha$ 求最大。

对于第一步，先令 $L(w,b,\alpha )$ 对 $w,b$ 求偏导为0，可得：
$w=\sum_{i=1}^{m}\alpha_{i}y_{i}x_{i},$

$0=\sum_{i=1}^{m}\alpha_{i}y_{i}.$

将此两个式子带入（2）式消去 $w,b$ 。便得到了（1）式的对偶问题。

$_{\alpha\geq 0 }^{max}\sum_{i=1}^{m}\alpha_{i}-\frac{1} {2}\sum_{i,j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j}$

$s.t. \sum_{i=1}^{m}\alpha_{i}y_{i}.=0,$
$\alpha_{i}\geq 0 , i = 1,2,...,m$

类比来看，我们的目标函数没有 $h(x) = 0$ 的等式约束。
于是，上面的过程，需要满足的KKT条件是

$\left\{\begin{matrix}\alpha_{i} \geq 0 ;\\1- y_{i}( w^{T}x_{i}+b) \leq 0;\\ \alpha_{i}(1-y_{i}( w^{T}x_{i}+b))=0.\end{matrix}\right.$

我们看到，对于任意样本，总有 $\alpha_{i} = 0$ 或者 $y_{i}( w^{T}x_{i}+b) =1$ .若 $\alpha_{i} = 0$ ，则由 $w=\sum_{i=1}^{m}\alpha_{i}y_{i}x_{i},$ 知 $w = 0$ , 则此 $\alpha_{i}$ 对应的向量不会对 $f(x)$ 的确定有任何影响。而 $\alpha_{i} > 0$ 时，必有 $y_{i}( w^{T}x_{i}+b) =1$ ，此时 $\alpha_{i}$ 对应的向量在最大间隔的边缘上（一开始示意图的虚线上），即是支持向量。这也说明，最终模型的确定，只与支持向量有关。

接下来，怎么求 $\alpha$ 呢？

SMO算法

先写到这里，下次再继续。

参考博文：
机器学习中的线性代数之矩阵求导 https://blog.csdn.net/u010976453/article/details/54381248
周志华老师的《机器学习》

支持向量机（SVM）从入门到放弃再到掌握

前言

SVM由线性分类开始

凸优化

对偶问题

KKT条件

SMO算法

猜你喜欢