UVA11426 GCD - Extreme (II)

版权声明：蒟蒻写文章不容易啊，各位大佬转载要告诉我一声,QAQ https://blog.csdn.net/qq_38944163/article/details/83756739

我扔：https://www.luogu.org/problemnew/show/UVA11426

题目的大意就是求

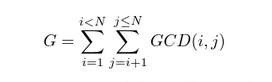
 先别急着打莫比乌斯反演，这题有更简单的做法，可以先设

答案

我们首先考虑如何求

我们可以先把的值分类，我们发现肯定是的约数，再设表示的小于n的正整数的个数，

显然

扫描二维码关注公众号，回复： 4748903 查看本文章

可以注意到, 和 n / i 互质的数的个数即为个，然后这题就切掉了

#include<bits/stdc++.h>
#define N 1000005
using namespace std;
int prime[N], phi[N], vis[N], sz;
void get_phi(){
	vis[1] = 1;
	for(int i = 2; i < N; i ++){
		if(!vis[i]){
			prime[++ sz] = i;
			phi[i] = i - 1;
		}
		for(int j = 1; j <= sz && prime[j] * i < N; j ++){
			vis[prime[j] * i] = 1;
			if(i % prime[j] == 0){
				phi[i * prime[j]] = phi[i] * prime[j];
				break;
			}
			phi[i * prime[j]] = phi[i] * (prime[j] - 1);
		}
	}
}//-------------------------------------------以上部分为线性筛质数
long long n, f[N], s[N];
int main(){
	get_phi();
	for(int i = 1; i < N; i ++)
		for(int j = i * 2; j < N; j += i)
			f[j] += i * phi[j / i]; 
//-------------------------------------------------即算每个数i对i的倍数的贡献
	for(int i = 1; i < N; i ++) s[i] = s[i-1] + f[i];
//-------------------------------------------------s[i]即为答案
	while(scanf("%lld", &n) == 1 && n){
		printf("%lld\n", s[n]);//O(1)输出
	}	
	return 0;
}

好题啊……GCD - Extreme  GCD - Extreme (I) GCD - Extreme (II) 可以用同一份代码A掉