机器学习最优化方法[3]--约束优化

考虑一个优化问题： $\min_{x}f(x)$， 我们一般对 $x$求导，导数为0的点即为极值点。当遇到导数不好求出的时候，我们一般用梯度下降法或者牛顿法等迭代的方法。这些都是没有约束的最优化解法，当我们对自变量有一定约束的时候应该如何求解是本文要讨论的问题。

1、等式约束

求解如下有等式约束的最小化问题： $\min_xf(x)$ $s.t. \quad h(x)=0$

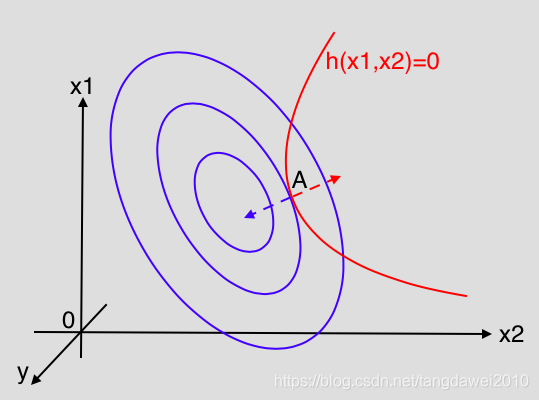
假设 $x$是二维空间向量，那么 $y=f(x)$是三维空间中的一个曲面。如图所示，蓝色曲线为等高线，红色部分是约束 $h(x)=0$。满足 $f(x)$最小的 $x$的值必须在红色曲线上，所以 $x$要么是等高线与 $h(x)=0$的交点，要么是切点。但是交点是不可能的，因为如果是交点，则一定还有另一条等高线与之相交并等到更接近最小值的 $x$, 因此最接近最小值的 $x$一定是两条曲线的切点，即在这个点两条曲线有相同的切线，因此法向量方向相同，可以得出：
$\nabla f(x)=\lambda \nabla h(x), \lambda \geq0$
我们也可以写为：
$\nabla f(x)+\alpha \nabla h(x)=0$
加上我们的约束条件: $h(x)=0$, 我们只需要解如下方程组即可得到 $x$的解：
$\begin{cases} \nabla f(x)+\alpha \nabla h(x)=0\\ h(x)=0\\ \end{cases}$
再回到原问题，我们可以构造函数：
$L(x,\alpha)=f(x)+\alpha h(x)$
分别对 $x$和 $\alpha$求偏导数，并令偏导数为0：
$\begin{cases} \nabla_x L(x,\alpha)=0\\ \nabla_{\alpha} L(x,\alpha)=0\\ \end{cases} \Rightarrow \begin{cases} \nabla f(x)+\alpha \nabla h(x)=0\\ h(x)=0\\ \end{cases}$
跟我们前面推导的方程组完全相同，该方法就是拉格朗日乘子法， $L(x,\alpha)$被称为拉格朗日函数。
当存在多个等式约束的时候，记为 $h_i(x)=0, i=0,1,..., m$，同样的我们构造拉格朗日函数：
$L(x,\alpha)=f(x)+\sum_{i=0}^{m}\alpha_i h_i(x)$
然后分别对 $x$和 $\alpha_i, i=0,1,...,m$求偏导数，令偏导数为0求解方程组即可。

2、不等式约束

加上不等式约束之后，我们的问题变为： $\min_xf(x)$ $s.t. \quad g(x)\leq0$
当然任何大于 $\geq 0$的约束我们都可以转化为 $\leq 0$的约束，这里我们统一用 $g(x)\leq0$作为不等式约束。
对于不等式约束， $x$的可行解有两种情况：
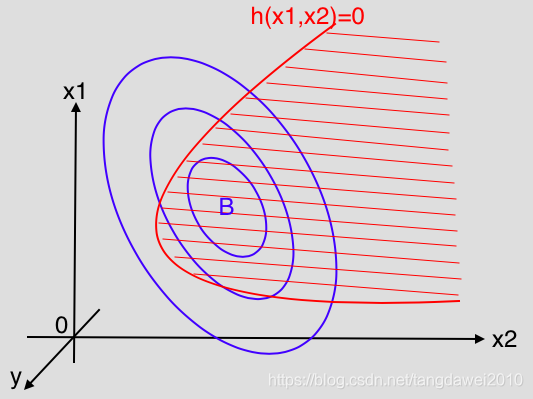
(1) $f(x)$本身的极值点落在约束范围之内，如下图，此时约束不起任何作用，我们直接用梯度下降法求解 $f(x)$的极值即可。

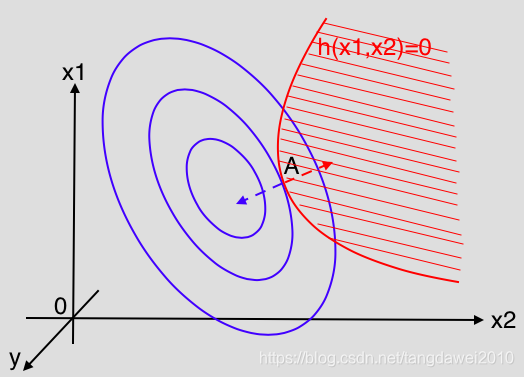
(2) $f(x)$本身的极值点在约束范围之外，如下图所示，此时在此约束条件下的极值点一定落在约束边界 $g(x)=0$上，而此时的极值点等同于等式约束下的极值点，可以用拉格朗日乘子法求出。

现在我们讨论在等式约束和不等式约束同时存在的情况，最优化问题变为：
$\min_xf(x)$ $s.t. \quad h_i(x)=0, i=0,1,...,m$ $\quad \quad g_j(x)\leq 0, i=0,1,...,n$
构造拉格朗日函数：
$L(x,\alpha,\beta)=f(x)+\sum_{i=0}^{m}\alpha_i h_i(x)+\sum_{j=0}^{n}\beta_j g_j(x)$
如果要求得 $x$的可行解，需要满足如下条件：
$\nabla _xL(x,\alpha,\beta)=0 \qquad\quad(1)\\ h_i(x)=0 \qquad \qquad \qquad(2)\\ g_j(x)\leq0 \qquad \qquad \qquad(3)\\ \beta_jg_j(x)=0 \qquad \qquad \quad(4)\\ \beta_j\geq0 \qquad \qquad \qquad\quad(5)$
这些条件便是KKT(Karush-Kuhn-Tucker)条件, 其中(1)是拉格朗日函数取得最优解的必要条件，(2)和(3)是原问题的约束条件，(4)是松弛互补条件，(5)是对拉格朗日乘子的约束。

KKT条件是优化问题取得极值的必要条件(当原问题是凸问题的时候就是充分必要条件)，也就是说只要满足KKT条件，便可以用拉格朗日乘子法求得极值点。